查找算法介绍

在 java 中，我们常用的查找有四种:
1) 顺序(线性)查找
2) 二分查找/折半查找
3) 插值查找
4) 斐波那契查找

一、线性(顺序)查找算法

源代码：OrderSearch.java

1、题意说明

有一个数列： {1,8,10, 89,1000,1234} ，判断数列中是否包含此名称【顺序查找】 要求: 如果找到了，就提
示找到，并给出下标值。

2、代码实现

说明：就是普通的遍历查找，找到返回下标，没有找到返回-1，之后判断即可

  1. package search;
  3. public class OrderSearch {
  5.     public static void main(String[] args) {
  6.         int[] arr = {1,8,10, 89,1000,1234};
  7.         int search = orderSearch(arr, 134);
  8.         if(search != -1) {
  9.             System.out.println("找到对应下标,下标为："+search);
  10.         }else {
  11.             System.out.println("没有找到对应下标");
  12.         }
  13.     }
  15.     /**
  16.      * 
  17.      * @Description 顺序查找
  18.      * @auther changlu
  19.      * @date Aug 21, 202010:16:13 AM
  20.      * @param arr 数组
  21.      * @param value 查找值
  22.      * @return 返回下标
  23.      */
  24.     public static int orderSearch(int[] arr,int value) {
  25.         for(int i=0;i<arr.length;i++) {
  26.             if(value == arr[i]) {
  27.                 return i;//找到返回下标
  28.             }
  29.         }
  30.         return -1;//没有找到
  31.     }
  32. }

运行结果：
QQ截图20200821102055.jpg

二、二分查找算法

源代码(优化前+优化后)：BinarySearch.java

1、二分查找算法的思路

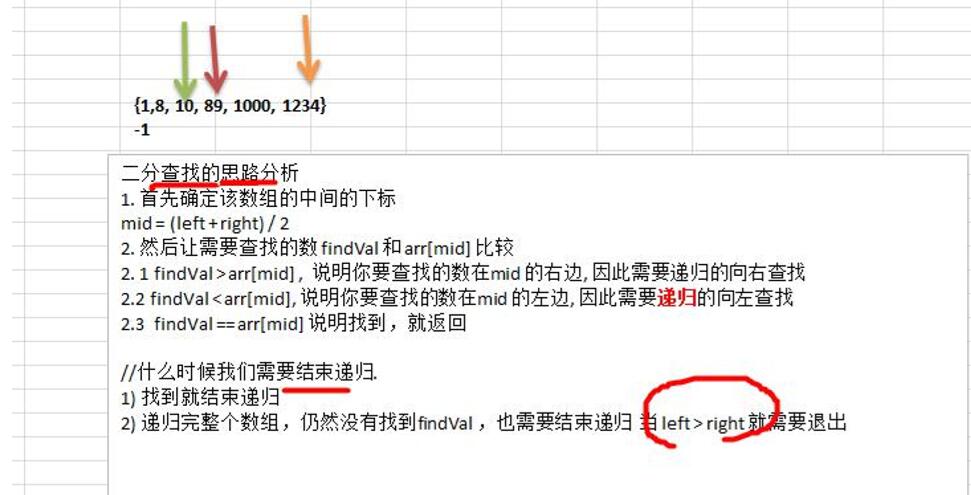
QQ截图20200821104621.jpg

2、题意描述

请对一个有序数组进行二分查找 {1,8,10,89,1000,1234} ，输入一个数看看该数组是否存在此数，并且求出下 标，如果没有就提示”没有这个数”。

3、代码实现(递归解决，只能查找一个指定值的下标)

说明：找到值返回下标，没有找到返回-1

  1. package search;
  3. public class BinarySearch {
  5.     public static void main(String[] args) {
  6.         int[] arr = {1,8,10, 89,1000,1234};
  7.         int binarySearch = binarySearch(arr, 0, arr.length-1, 1234);
  8.         if(binarySearch != -1) {
  9.             System.out.println("找到该值，下标为："+binarySearch);
  10.         }else {
  11.             System.out.println("没有找到该值!");
  12.         }
  13.     }
  16.     public static int binarySearch(int[] arr,int left,int right,int findValue) {
  17.         if(left>right) {
  18.             return -1;
  19.         }
  20.         int mid = (left+right)/2;
  21.         if(findValue == arr[mid]) {
  22.             return mid;
  23.         }else if(findValue < arr[mid]) {
  24.             return binarySearch(arr, left, mid-1, findValue);
  25.         }else {
  26.             return binarySearch(arr, mid+1, right, findValue);
  27.         }
  28.     }
  29. }

运行结果：
QQ截图20200821104824.jpg

4、代码优化(递归，能够查找多个指定值的下标)

情况说明：
对于上一个代码实现还有着缺陷的地方，只能查找最左边第一个的值，如果有连续多个相同值的话就无法找到，所以这里进行优化：
在找到第一个值的情况下，通过左右依次向前向后循环判断添加到list集合中，再进行返回。

思路分析：
QQ截图20200821111456.jpg

代码实现：
说明：可以看到在第三个else也就是访问到第一个指定值时进行前后循环判断遍历即可

  1. package search;
  3. import java.util.ArrayList;
  4. import java.util.List;
  6. public class BinarySearch {        
  7.     //能够将多个相同的值的下标存放到list集合中返回
  8.     public static List<Integer> binarySearch2(int[] arr,int left,int right,int findValue) {
  9.         if(left>right) {
  10.             return new ArrayList<>();//如果没有找到对应值，返回空的list集合
  11.         }
  12.         int mid = (left+right)/2;
  13.         if(findValue > arr[mid]) {
  14.             return binarySearch2(arr, mid+1, right, findValue);
  15.         }else if(findValue < arr[mid]) {
  16.             return binarySearch2(arr, left, mid-1, findValue);
  17.         }else {
  18.             //创建一个list集合用来存放对应值下标
  19.             List<Integer> list = new ArrayList<>();
  20.             //向左进行查找
  21.             int temp = mid-1;
  22.             while(true) {
  23.                 //如果temp值小于0或不等于查找的值直接break退出
  24.                 if(temp<0||arr[temp] != findValue) {
  25.                     break;
  26.                 }
  27.                 list.add(temp--);//符合要求添加下标
  28.             }
  29.             list.add(mid);//添加mid之前符合的值的下标再添加mid的下标
  30.             //向右进行查找
  31.             temp = mid+1;
  32.             while(true) {
  33.                 //如果temp值小于0或不等于查找的值直接break退出
  34.                 if(temp>=arr.length||arr[temp] != findValue) {
  35.                     break;
  36.                 }
  37.                 list.add(temp++);//符合要求添加下标
  38.             }
  39.             //返回集合
  40.             return list;
  41.         }
  42.     }
  43. }

测试代码：

  1. package search;
  3. import java.util.ArrayList;
  4. import java.util.List;
  6. public class BinarySearch {
  8.     public static void main(String[] args) {
  9.         int[] arr = {1,8,10, 1000,1000,1000,1234};
  10.         List<Integer> list = binarySearch2(arr, 0, arr.length-1, 1111);
  11.         System.out.println("list中的下标为："+list);
  12.     }
  13. }

运行结果：
QQ截图20200821111731.jpg

三、插值查找算法(优化二分法)

源代码：BinarySearch.java

1、原理介绍

QQ截图20200822173955.jpg

主要核心：int mid = left+(findValue-arr[left])*(right-left)/(arr[right]-arr[left]);
**

2、 举例说明插值查找算法 1-100 的数组

QQ截图20200822174103.jpg

3、代码实现

说明：主要是对于mid查找作了优化，是根据查找值通过斜率的方式来查找，两个注意点说明。
① 对于判断left>right这里，增加两个条件必须有就是判断查找值是否越界，如果不做处理会出现越界情况
② 对于mid求值更加复杂一些，可以看上面原理介绍进行记忆

  1.     //使用差值查找
  2.     public static int binarySearch3(int[] arr, int left, int right, int findValue) {
  3.         //在差值查找中不能设置超过指定范围的值，可能会出现越界问题
  4.         if (left > right || findValue<arr[0] || findValue>arr[arr.length-1]) {//修改点1
  5.             return -1;
  6.         }
  7.         int mid = left+(findValue-arr[left])*(right-left)/(arr[right]-arr[left]);//修改点2
  8.         if (findValue == arr[mid]) {
  9.             return mid;
  10.         } else if (findValue < arr[mid]) {
  11.             return binarySearch1(arr, left, mid - 1, findValue);
  12.         } else {
  13.             return binarySearch1(arr, mid + 1, right, findValue);
  14.         }
  15.     }

测试代码：

  1. package search;
  3. import java.util.ArrayList;
  4. import java.util.List;
  6. public class BinarySearch {
  8.     public static void main(String[] args) {
  9.         int[] arr = {1,8,10, 89,1000,1234};
  10.         int binarySearch = binarySearch3(arr, 0, arr.length-1, 1);
  11.         if(binarySearch != -1) {
  12.             System.out.println("找到该值，下标为："+binarySearch);
  13.         }else {
  14.             System.out.println("没有找到该值!");
  15.         }
  16.     }
  17. }

运行结果：
QQ截图20200822174439.jpg

四、斐波那契(黄金分割法)查找算法(不太明白)

1、斐波那契(黄金分割法)查找基本介绍

QQ截图20200824144152.jpg

2、斐波那契(黄金分割法)原理

QQ截图20200824144223.jpg
QQ截图20200824144304.jpgQQ截图20200824144316.jpg

3、斐波那契查找应用案例

题目说明：请对一个有序数组进行斐波那契查找 {1,8,10,89,1000,1234} ，输入一个数看看该数组是否存在此数，并且求 出下标，如果没有就提示”没有这个数”。

说明：这里包含两个方法，一个方法是获取到前20位斐波那契数，第二个方法是通过斐波那契数组来寻找黄金分割点进行值的查找。

  1. package search;
  2. import java.util.Arrays;
  3. public class FibonacciSearch {
  4.     private static int maxSize = 20;
  5.     //创建一个斐波那契数组
  6.     public static int[] fib(){ 
  7.         int[] f = new int[maxSize];
  8.         f[0] = 1;
  9.         f[1] = 1;
  10.         for(int i=2;i<maxSize;i++) {
  11.             f[i] = f[i-1]+f[i-2];
  12.         }
  13.         return f;
  14.     }
  16.     public static int fibSearch(int[] a, int key) {
  17.         int low = 0;
  18.         int high = a.length - 1;
  19.         int k = 0;// 表示斐波那契分割数值的下标
  20.         int mid = 0;
  21.         int[] f = fib();// 获取到斐波那契数组
  22.         // 获取到斐波那契
  23.         while (high > f[k] - 1) {
  24.             k++;
  25.         }
  27.         // 重新生成一个新的指定为f数组中的长度大小数组，多余的使用a数组的最后一位填充
  28.         int[] temp = Arrays.copyOf(a, f[k]);
  29.         // 举例:
  30.         // temp={1,8,10,89,1000,1234,0,0} =>{1,8,10,89,1000,1234,1234,1234,}
  31.         for (int i = high + 1; i < temp.length; i++) {
  32.             temp[i] = temp[high];
  33.         }
  35.         while (low <= high) {
  36.             System.out.println("查找");
  37.             mid = low + f[k - 1] - 1;
  38.             if (key < temp[mid]) {// 如果实际值再左边
  39.                 high = mid-1;
  40.                 k--;
  41.             }else if(key>temp[mid]) {//这是往后面查找
  42.                 low = mid+1;
  43.                 k-=2;
  44.             }else {//找到的情况
  45.                 //需要确定，返回的是哪个下标
  46.                 if(mid<=high) {
  47.                     return mid;
  48.                 }else {
  49.                     return high;
  50.                 }
  52.             }
  53.         }
  54.         return -1;//没有找到
  55.     }
  56. }



测试代码：

  1. package search;
  2. import java.util.Arrays;
  3. public class FibonacciSearch {
  4.     public static void main(String[] args) {
  5.         int[] arr = {1,8,10,89,1000,1234};
  6.         int fibSearch = fibSearch(arr, 1234);
  7.         System.out.println(fibSearch);
  8.     }
  9. }

运行结果：5


整理者：长路 时间：2020/8/21-2020/8/24