一、 二分查找算法(非递归)

二分查找算法(非递归)介绍

QQ截图20200904193842.jpg

二分查找算法(非递归)代码实现

数组 {1,5,8,9,10,20}, 编程实现二分查找， 要求使用非递归的方式完成.

  1. package xyz.changlu.binarySearchAlgorithm;
  3. public class BinarySearch {
  5.     public static void main(String[] args) {
  6.         int[] arr = {1,5,8,9,10,20};
  7.         int valueCur = binarySearch(arr, 30);
  8.         if(valueCur != -1) {
  9.             System.out.println("找到值为1的位置，位置为："+valueCur);
  10.         }else {
  11.             System.out.println("未找到值为1的位置");
  12.         }
  13.     }
  15.     //非递归进行查找
  16.     public static int binarySearch(int[] arr,int findValue) {
  17.         int left = 0;
  18.         int right = arr.length-1;
  19.         while(left<=right) {
  20.             int mid = (left+right)/2;
  21.             //如果找到了
  22.             if(findValue == arr[mid]) {
  23.                 return mid;//返回下标
  24.             }else if(findValue<arr[mid]) {//如果查找值比中间值小
  25.                 right = mid - 1;
  26.             }else {//如果查找值比中间值大
  27.                 left = mid + 1;
  28.             }
  29.         }
  30.         return -1;
  31.     }
  32. }

运行结果：
QQ截图20200904194008.jpg
**

二、分治算法

1、分治算法介绍

QQ截图20200906091050.jpg

2、分治算法的基本步骤

分治法在每一层递归上都有三个步骤：
1) 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
2) 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3) 合并：将各个子问题的解合并为原问题的解。

3、分治(Divide-and-Conquer(P))算法设计模式如下

QQ截图20200906091208.jpg

4、汉诺塔(分治)

汉诺塔的传说

QQ截图20200906095300.jpg

汉诺塔游戏的演示和思路分析

QQ截图20200906095324.jpg

代码实现

说明：采用了分治的算法，层层递归下去

  1. package xyz.changlu.dac;
  3. public class Hanoitower {
  4.     public static void main(String[] args) {
  5.         hanoitower(3, 'a', 'b', 'c');
  6.     }
  8.     public static void hanoitower(int n, char a, char b, char c) {
  9.         if (n == 1) {
  10.             System.out.println(a + "->" + c);
  11.         } else {
  12.             hanoitower(n - 1, a, c, b);
  13.             System.out.println(a + "->" + c);
  14.             hanoitower(n - 1, b, a, c);
  15.         }
  17.     }
  18. }

三、动态规划算法

1、应用场景-背包问题

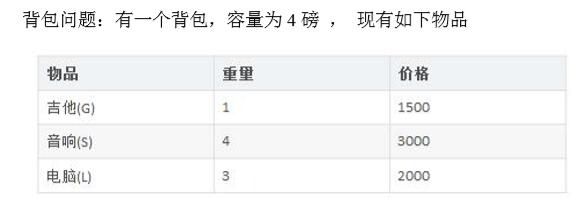
QQ截图20200906111248.jpgQQ截图20200906111300.jpg

2、动态规划算法介绍

QQ截图20200906111334.jpg

3、动态规划算法最佳实践-01背包问题

题意分析

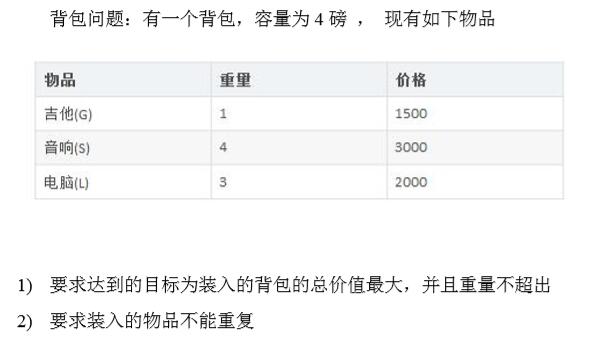
QQ截图20200906111459.jpg
注意这里的两个要求，物品不能重复以及背包总价值最大且重量不超出

思路分析和图解(包含示例)

QQ截图20200906153131.jpgQQ截图20200906153144.jpg

示例：
QQ截图20200906153225.jpg

代码实现

源代码：KnapsackProblem.java

(1)打印填充的对应表(未完善)

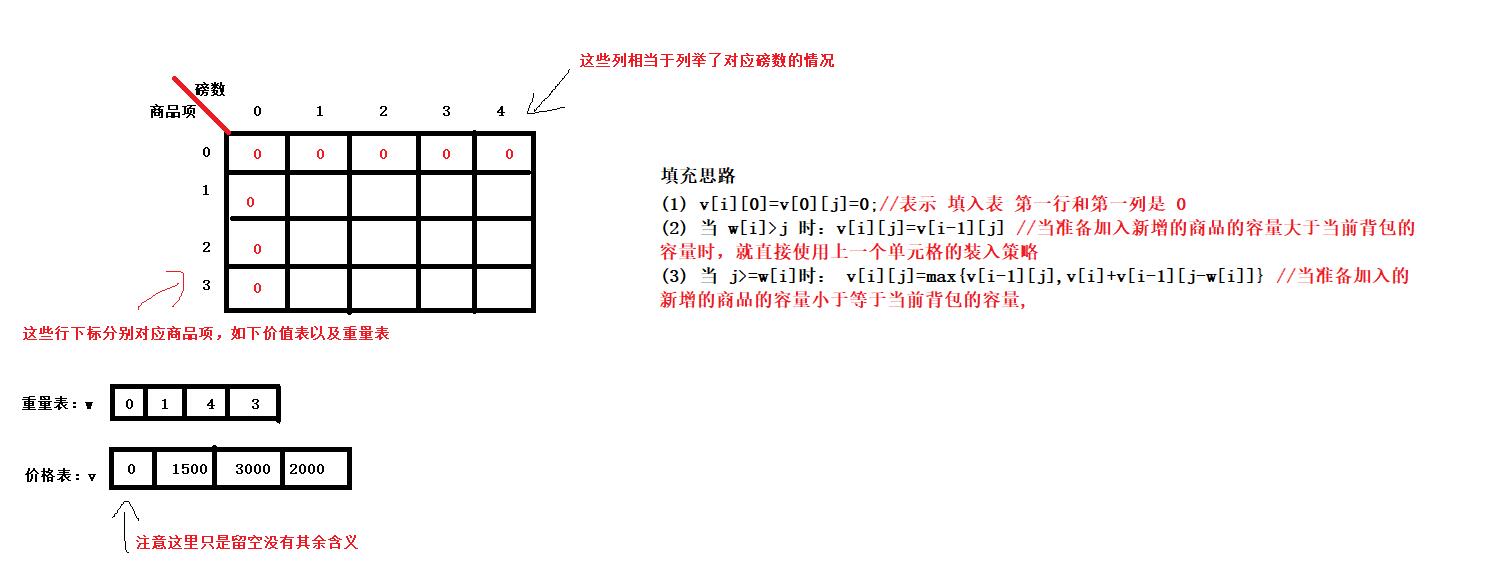
QQ截图20200906154812.jpg

  1. package dynamic;
  3. //背包问题
  4. public class KnapsackProblem {
  5.     public static void main(String[] args) {
  6.         //设置一维数组  分别是记录商品的价格(v表示value)以及商品的重量(w表示weight)
  7.         //注意这里第一个位置留空为0 有用数据为下标0之后的
  8.         int[] v = {0,1500,3000,2000};
  9.         int[] w = {0,1,4,3};
  10.         int n = 4;//表示背包中能够存放4磅物品
  11.         int m = v.length-1;//用于表示有几件商品
  13.         //定义一个二维数组 用来存放商品的总金额  
  14.         //行下标1 2 3对应着的v数组的下标1 2 3   行数为商品数量
  15.         //列下标1 2 3 4代表着1磅 2磅 3磅 4磅等情况  列数为总磅数数量
  16.         int[][] vs = new int[m+1][n+1];//行列都需要空出来一行一列为0
  18.         //行列从第一行第一列开始计算
  19.         for(int i = 1;i<vs.length;i++) {
  20.             for(int j = 1;j<vs[i].length;j++) {
  21.                 //如果要添加的商品大于当前列对应磅数 来存取上一件物品(i-1)对应的金额
  22.                 if(w[i]>j) {
  23.                     vs[i][j] = vs[i-1][j];
  24.                 }else if(j>=w[i]) {
  25.                     //vs[i-1][j]与v[i]+vs[i-1][j-w[i]]作比较
  26.                     //vs[i-1][j]表示对应磅数上一件物品的存取金额
  27.                     //v[i]+vs[i-1][j-w[i]] 表示当前物品金额+上一件物品的(当前列磅数-当前物品磅数)位置的存放金额
  28.                     vs[i][j] = Math.max(vs[i-1][j], v[i]+vs[i-1][j-w[i]]);
  29.                 }
  30.             }
  31.         }
  33.         //用于打印二维数组数据
  34.         for (int i = 0; i < vs.length; i++) {
  35.             for (int j = 0; j < vs[i].length; j++) {
  36.                 System.out.print(vs[i][j]+" ");
  37.             }
  38.             System.out.println();
  39.         }
  40.     }
  41. }

运行结果：
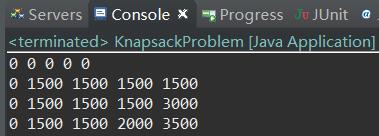
QQ截图20200906154924.jpg

(2)打印出对应背包的商品项(完善)

修改部分：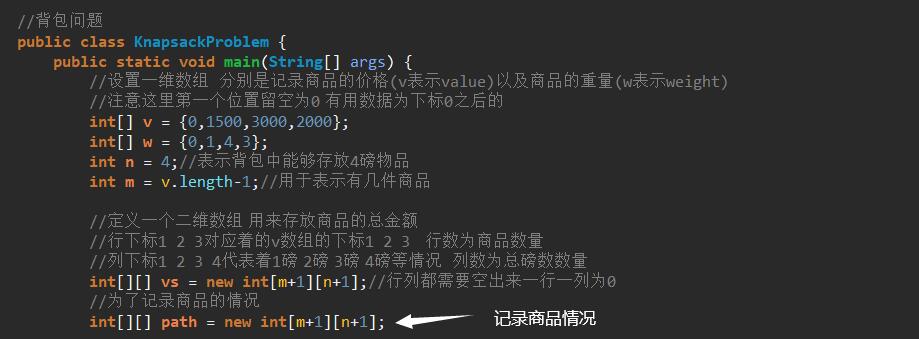
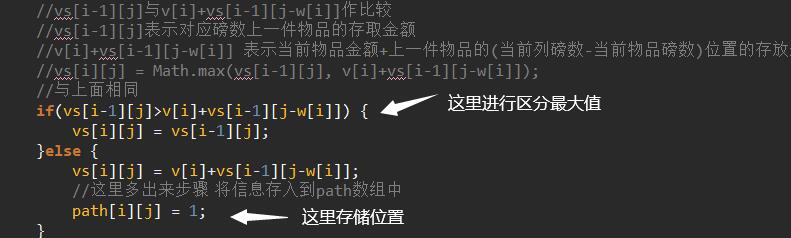
QQ截图20200906155507.jpgQQ截图20200906155543.jpgQQ截图20200906155601.jpg
对应path表的值：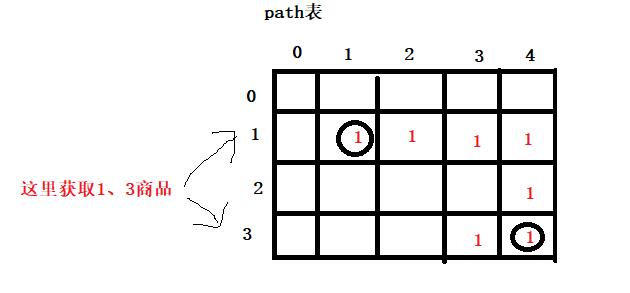
QQ截图20200906160028.jpg

  1.     package dynamic;
  3.     //背包问题
  4.     public class KnapsackProblem {
  5.         public static void main(String[] args) {
  6.             //设置一维数组  分别是记录商品的价格(v表示value)以及商品的重量(w表示weight)
  7.             //注意这里第一个位置留空为0 有用数据为下标0之后的
  8.             int[] v = {0,1500,3000,2000};
  9.             int[] w = {0,1,4,3};
  10.             int n = 4;//表示背包中能够存放4磅物品
  11.             int m = v.length-1;//用于表示有几件商品
  13.             //定义一个二维数组 用来存放商品的总金额  
  14.             //行下标1 2 3对应着的v数组的下标1 2 3   行数为商品数量
  15.             //列下标1 2 3 4代表着1磅 2磅 3磅 4磅等情况  列数为总磅数数量
  16.             int[][] vs = new int[m+1][n+1];//行列都需要空出来一行一列为0
  17.             //为了记录商品的情况
  18.             int[][] path = new int[m+1][n+1];
  20.             //行列从第一行第一列开始计算
  21.             for(int i = 1;i<vs.length;i++) {
  22.                 for(int j = 1;j<vs[i].length;j++) {
  23.                     //如果要添加的商品大于当前列对应磅数 来存取上一件物品(i-1)对应的金额
  24.                     if(w[i]>j) {
  25.                         vs[i][j] = vs[i-1][j];
  26.                     }else if(j>=w[i]) {
  27.                         //vs[i-1][j]与v[i]+vs[i-1][j-w[i]]作比较
  28.                         //vs[i-1][j]表示对应磅数上一件物品的存取金额
  29.                         //v[i]+vs[i-1][j-w[i]] 表示当前物品金额+上一件物品的(当前列磅数-当前物品磅数)位置的存放金额
  30.                         //vs[i][j] = Math.max(vs[i-1][j], v[i]+vs[i-1][j-w[i]]);
  31.                         //与上面相同
  32.                         if(vs[i-1][j]>v[i]+vs[i-1][j-w[i]]) {
  33.                             vs[i][j] = vs[i-1][j];
  34.                         }else {
  35.                             vs[i][j] = v[i]+vs[i-1][j-w[i]];
  36.                             //这里多出来步骤 将信息存入到path数组中
  37.                             path[i][j] = 1;
  38.                         }
  39.                     }
  40.                 }
  41.             }
  43.             //用于打印二维数组数据
  44.             for (int i = 0; i < vs.length; i++) {
  45.                 for (int j = 0; j < vs[i].length; j++) {
  46.                     System.out.print(vs[i][j]+" ");
  47.                 }
  48.                 System.out.println();
  49.             }
  51.             System.out.println("============================");
  52.             //获取到行数列数
  53.             int i = path.length-1;
  54.             int j = path[0].length-1;
  55.             //从path的最后开始找
  56.             while(i>0&&j>0) {
  57.                 if(path[i][j] == 1) {
  58.                     System.out.println("移入"+i+"到背包");
  59.                     j -= w[i];
  60.                 }
  61.                 i--;
  62.             }
  63.         }
  64.     }

运行结果：
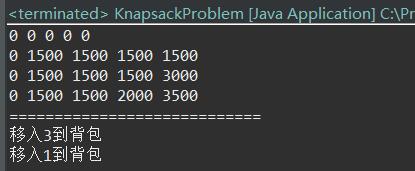
QQ截图20200906155643.jpg

四、kmp算法(解决两个字符串匹配)

应用场景-字符串匹配问题

QQ截图20200909145850.jpg

第一种解决方法(暴力匹配)

解决思路

QQ截图20200909145922.jpg

代码实现

  1. package kmp;
  3. public class ViolenceMatch {
  5.     public static void main(String[] args) {
  6.         String str1 = "硅硅谷 尚硅谷你尚硅 尚硅谷你尚硅谷你尚硅你好"; 
  7.         String str2 = "尚硅谷你尚硅你";
  8.         int index = violenceMatch(str1, str2);
  9.         System.out.println("对应位置为："+index);
  10.     }
  12.     //进行暴力匹配字符串
  13.     public static int violenceMatch(String str1,String str2) {
  14.         //将字符串转为char型数组
  15.         char[] c1 = str1.toCharArray();
  16.         char[] c2 = str2.toCharArray();
  18.         //获取两个字符数组的长度
  19.         int len1 = c1.length;
  20.         int len2 = c2.length;
  21.         //设置两个移标来指向两个字符数组 i指向c1  j指向c2
  22.         int i = 0;
  23.         int j = 0;
  25.         //通过两个移标越界判断结束
  26.         while(i<len1 && j<len2) {
  27.             //判断两个移标指向位置是否相同
  28.             if(c1[i] == c2[j]) {
  29.                 i++;
  30.                 j++;
  31.             }else {
  32.                 //不相同的情况
  33.                 i = i-j+1;//这里从原本位置向后移一位
  34.                 j = 0;
  35.             }
  36.         }
  38.         //如果while出来j对应下标为c2的长度那么就说明全部字段都匹配到了
  39.         if(j == len2) {
  40.             //从而获取c1中初始匹配到的位置
  41.             return i-j;
  42.         }else {
  43.             //没有找到返回-1
  44.             return -1;
  45.         }
  46.     }
  48. }

运行结果：
QQ截图20200909150024.jpg

第二种解决方法(kmp算法) 未懂

整理者：长路 时间：2020/9/4-2020/9/6