时间大比拼
| 算法 | 八万数据 | 八十万数据 | 八百万数据 |
|---|---|---|---|
| 冒泡排序 | 9秒 | ||
| 选择排序 | 1秒不到 | ||
| 插入排序 | 2秒不到 | ||
| 希尔排序(交换法) | 22秒 | ||
| 希尔排序(移位法) | 0.1秒不到 | 0.16-0.184秒 | 2.232秒左右 |
| 快速排序 | 0.1秒左右 | 0.15秒不到 | 1.1-1.153秒 |
| 归并排序 | 0.014-0.016秒 | 0.11-0.114秒 | 1.227-1.804秒 |
| 基数排序(桶排序进阶) | 0.013、0.031、0.029秒 | 0.069、0.07、0.173秒 | 0.947、0.459、0.454秒 |
字节、kb、M怎么换算字节
换算率约bai等于1000(1024),从大到小顺du序为T、zhiGB、MB(兆Zhao)、KB、B再小就是位了换算率约bai等于1000(1024),从大到小顺du序为T、zhiGB、MB(兆Zhao)、KB、B再小就是位了
int型为4个字节,字节为B
一、冒泡排序
源代码:BubbleSort.java
1、基本介绍(概述+优化)


2、演示冒泡过程的例子(图解)

3、冒泡排序应用实例
我们举一个具体的案例来说明冒泡法。我们将五个无序的数:3,9,-1,10,-2 使用冒泡排序法将其排成一个从小
到大的有序数列。
优化前
说明:就是不断的从小到后将最大的数不断提到最后,总共有n个数,优化前一定执行n-1次循环判断来不断将最大数冒到最后。
public class BubbleSort {// 未进行优化的冒泡排序public static void bubbleSort2(int[] arr) {// 设置辅助变量int temp = 0;for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
优化后
说明:之前的话是根据n-1次循环进行不断比大小,进行优化就是将剩余循环次数中早已经排序结束的进行结束,不要进行没有必要的判断,那么如果一次循环都没有进行替换改动,那么就说明已经数组已经完成了排序。
public class BubbleSort {// 进行优化的冒泡排序public static void bubbleSort1(int[] arr) {// 设置辅助变量int temp = 0;boolean flag = true;for (int i = 0; i < arr.length - 1; i++) {flag = true;for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;// 如果作改变的话设置为falseflag = false;}}// 如果有一次组没有进行转换那么直接退出循环if (flag) {break;}}}}
进行测试:
package sortExer;import java.util.Arrays;public class BubbleSort {public static void main(String[] args) {// int[] arr = { 3, 9, -1, 10, 20 };int[] arr = new int[80000];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 80000);}long begin = System.currentTimeMillis();bubbleSort2(arr);System.out.println("排序后的数组为:" + Arrays.toString(arr));long end = System.currentTimeMillis();System.out.println("花费的时间为:" + (end - begin)/1000);}}
运行结果:
总结说明
对于8万个数据经过测试需要时间为9秒左右,时间复杂度为O(n^2)
二、选择排序
源代码:SelectSort.java
1、基本介绍以及选择排序思想
介绍:选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。

简单来说就是执行n-1次循环,从每次循环的数据中找出一个最小的数字,之后一轮结束时来进行交换最小值到对应前面位置。
2、选择排序思路分析图
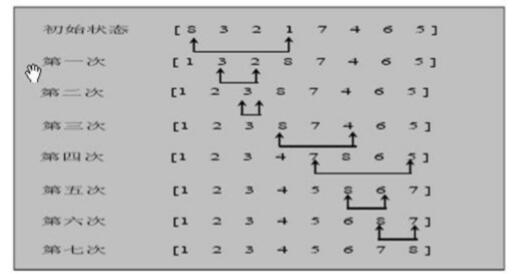

3、代码实现(包含优化)
说明:使用一个方法来封装选择排序
① 优化的部分就是最后判断是否先前设置min为最小值,如果判断不相等就不进行多余的交换。
② 在选择排序中比冒泡排序节省了许多的数据交换操作
package sortExer;import java.util.Arrays;public class SelectSort {public static void selSort(int arr[]) {//用来记录每次循环的最小下标int cur = 0;int min = 0;for(int i=0;i<arr.length-1;i++) {min = arr[i];//设置第一个值为最小值cur = 0;for(int j=i+1;j<arr.length;j++) {if(arr[j]<min) {min = arr[j];//min更新最小值cur = j;//设置最小值下标}}//如果最小值不是对应第i个值那么进行交换if(min!=arr[i]) {arr[cur] = arr[i];arr[i] = min;}}System.out.println("排序完成!!!");}}
测试:
package sortExer;import java.util.Arrays;public class SelectSort {public static void main(String[] args) {// int arr[] = {5,1,8,9,2};int[] arr = new int[80000];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 80000);}long begin = System.currentTimeMillis();//System.out.println("原先数组:"+Arrays.toString(arr));//进行选择排序selSort(arr);long end = System.currentTimeMillis();System.out.println("排序后数组:"+Arrays.toString(arr));System.out.println("花费时间为:"+(double)(end-begin)/1000+"秒");}}
运行结果:
总结说明
对于8万个数据经过测试需要时间为1秒不到,时间复杂度为O(n^2)
三、插入排序
源代码:InsertSort.java
1、插入排序法介绍与思想
介绍:插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。

2、插入排序思路图

3、代码实现
说明:这是从第一位开始不断获取之后的数字来与之前的列表进行比较再插入到之前列表中。
package sortExer;import java.util.Arrays;public class InsertSort {//插入排序封装实现public static void insertSort(int arr[]) {int val = 0;int insertIndex = 0;//默认从第1个开始不断向前插入for(int i=1;i<arr.length;i++) {//首先val获取到待插入的值val = arr[i];//用来表示待插入的位置insertIndex = i-1;//i大于等于0,且待插入值要小于之前的值while(insertIndex>=0 && val < arr[insertIndex]) {arr[insertIndex+1] = arr[insertIndex];insertIndex--;}arr[insertIndex+1] = val;}System.out.println("插入排序已经完成!!!");}}
测试:测试包含8万数据的数组进行排序
package sortExer;import java.util.Arrays;public class InsertSort {public static void main(String[] args) {// int arr[] = {5,4,1,9,8};// System.out.println("排序前:"+Arrays.toString(arr));// insertSort(arr);// System.out.println("排序后:"+Arrays.toString(arr));int[] arr = new int[80000];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 80000);}long begin = System.currentTimeMillis();insertSort(arr);long end = System.currentTimeMillis();System.out.println("排序后数组:"+Arrays.toString(arr));System.out.println("花费时间为:"+(double)(end-begin)/1000+"秒");}}
运行结果: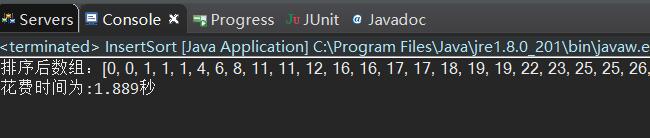
总结说明
对于8万个数据经过测试需要时间为2秒不到,时间复杂度为O(n^2)
四、希尔排序(Shell排序)
源代码:ShellSort.java
1、简单插入排序存在的问题

2、希尔排序法介绍与基本思想
希尔排序是希尔(DonaldShell)于 1959 年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
基本思想
3、希尔排序法的示意图
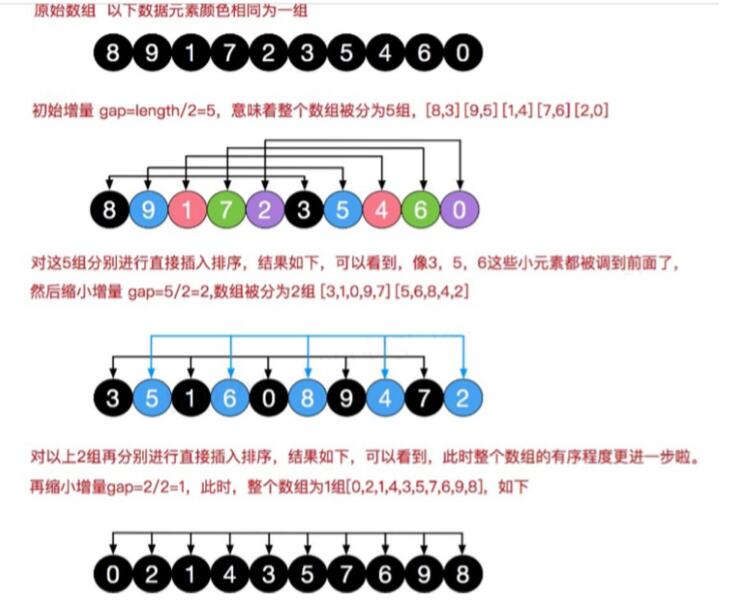

4、希尔排序法应用实例(2种)
① 使用交换法(与冒泡类似)
说明:使用对应位置的数不断的向前比较判断并且进行交换
package sortExer;import java.util.Arrays;public class ShellSort {、//使用希尔排序中的交换法public static void shellSort1(int arr[]) {int temp;int count = 0;//根据数组长度/2分组进行log2^n次排序for (int i = arr.length / 2; i > 0; i /= 2) {//从分组位置开始到数组最后for(int j = i;j<arr.length;j++)//不断从后往前根据分组的情况for(int k = j-i;k>=0;k-=i) {//从后往前进行比较将较大的数移至之后if(arr[k]>=arr[k+i]) {temp = arr[k];arr[k] = arr[k+i];arr[k+i] = temp;}}}System.out.println("希尔排序已经完成!!!");}}
② 使用移位法(与插入排序类似)
说明:与插入排序类似的方法进行将该插入的数据与之前对应的进行比较后移,找到合适的位置进行插入。
package sortExer;import java.util.Arrays;public class ShellSort {//使用希尔排序的移位法public static void shellSort2(int arr[]) {int cur = 0;int temp;//与之前交换法一致,这里是分的组数for(int i=arr.length/2;i>0;i/=2) {//找到对应的位置,之前以i为步数单位向前不断移位for(int j = i;j<arr.length;j++) {//记录初始位置的下标cur = j;temp = arr[j];//保存等会用于插入的值//根据条件不断向前移并进行比较,插入由j位置之前对应组中的while(cur-i>=0&&temp<arr[cur-i]) {arr[cur] = arr[cur-i];cur -=i;}if(cur != j) {arr[cur] = temp;}}}System.out.println("希尔排序->移位法已经完成");}}
两种方法的差距以及进行测试
测试方法:
package sortExer;import java.util.Arrays;public class ShellSort {public static void main(String[] args) {//int arr[] = {8,9,1,7,2,3,5,4,6,0};//shellSort(arr);int[] arr = new int[80000];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 80000);}long begin = System.currentTimeMillis();shellSort2(arr);long end = System.currentTimeMillis();System.out.println("排序后数组:"+Arrays.toString(arr));System.out.println("花费时间为:"+(double)(end-begin)/1000+"秒");}}
运行结果: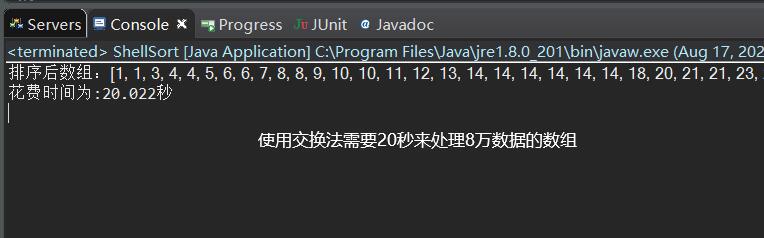
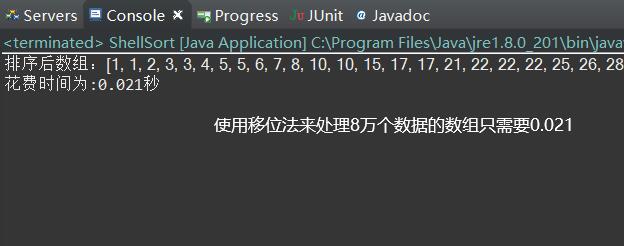
总结说明
对于8万个数据经过测试交换法需要时间22秒左右,移位法需要0.1秒不到的时间解决,时间复杂度为O(n^2),使用移位就不会像交换法一样大量的时间花费在两者交换之上吗,这一看差距就十分大了。
五、快速排序
源代码:QuickSort.java
1、快速排序法介绍

2、快速排序法示意图
主要需要使用递归的方法来进行
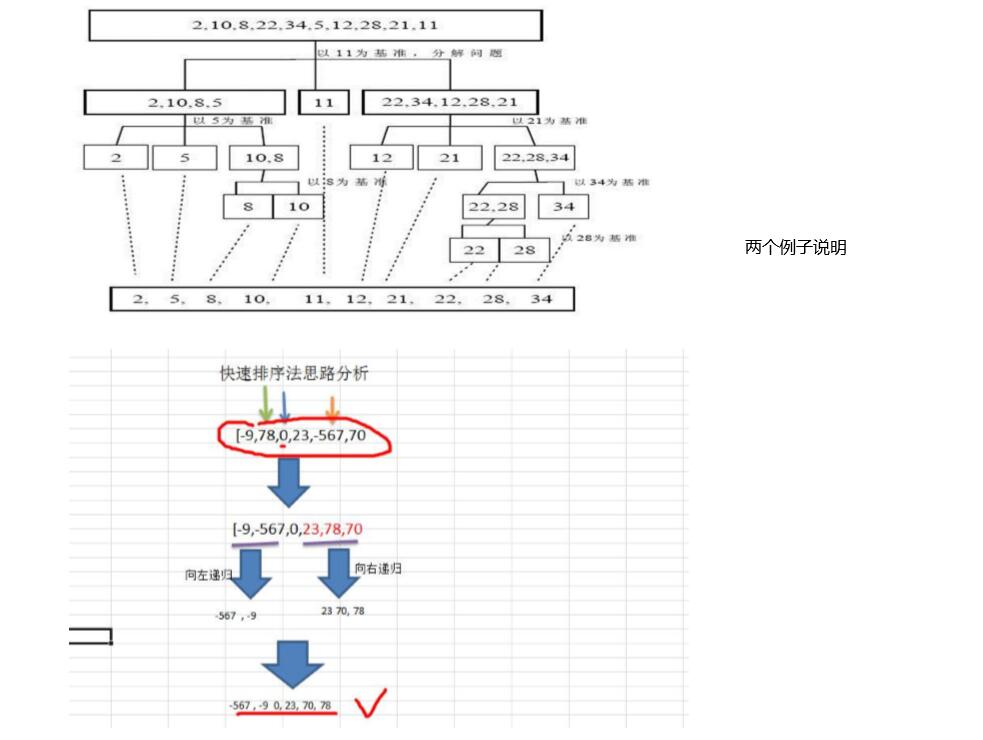
3、快速排序法应用实例


说明:这里的代码以left与right相加除二对应位置为基值,根据这个基值来从left以及right位置前后进行比较将小于基值的放在基值钱,大于的放在基值后,其中l==r的判断是都指向了基值的情况,其中还有若两个l与r都指向与基值相同且不再同一个位置的,相反位置进行前后增加。
package sortExer;import java.util.Arrays;public class QuickSort {public static void quickSort(int arr[],int left,int right) {int l = left;int r = right;int pirot = arr[(right+left)/2];int temp = 0;while(l<r) {while(arr[l]<pirot) l++;while(arr[r]>pirot) r--;//如果都指向到了中间的那个值时if(l==r) {l++;//l向右增加一位r--;//r向左增加一位break;//退出while}temp = arr[l];arr[l] = arr[r];arr[r] = temp;if(arr[l] == pirot) {r--;}if(arr[r] == pirot) {l++;}}//向左递归if(left<r) {quickSort(arr, left, r);}//向右递归if(right>l) {quickSort(arr, l, right);}}}
总结说明
快速排序比希尔排序在处理数据量更大的情况下更占优势
六、归并排序
源代码:MergeSort.java
1、归并排序介绍

2、示意图演示
归并排序思想示意图 1-基本思想
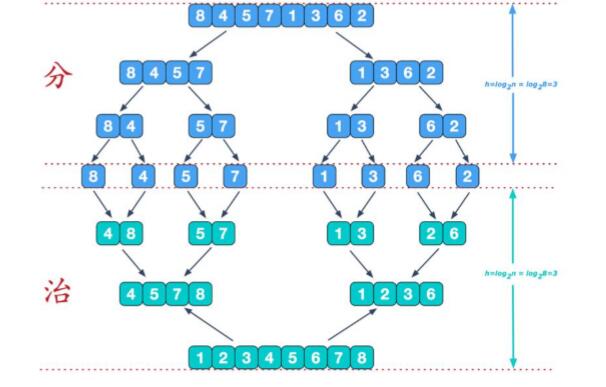
归并排序思想示意图 2-合并相邻有序子序列:
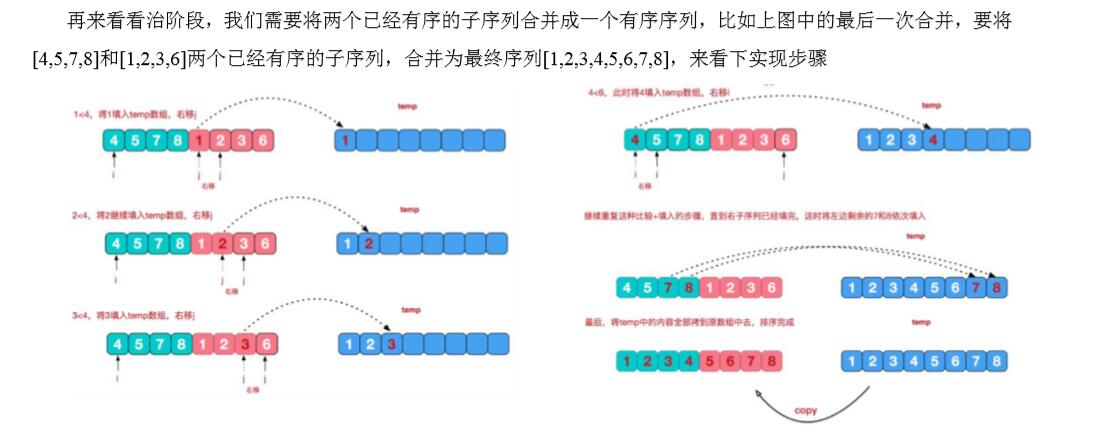
3、归并排序的应用实例
说明:对于归并排序,采用了分治的方法,在这里使用到了两个方法,一个是进行合的方法用于处于从最初2个值进行合并到最后所有的都按照规定排序方法递归回来。
package sortExer;import java.util.Arrays;public class MergeSort {//分+合方法public static void mergeSort(int []arr,int left,int right,int []temp) {//这里设置if(left<right) {int mid = (left+right)/2;//向左递归开始分解mergeSort(arr, left, mid, temp);//向右递归开始分解mergeSort(arr, mid+1, right, temp);//最后进行合并Merge(arr, left, mid, right, temp);// for(int i =left;i<=right;i++) { //打印出进行合并的情况// System.out.printf("%d ",arr[i]);// }// System.out.println();}}/**** @Description 和的方法* @auther changlu* @date Aug 19, 202010:56:51 AM* @param arr 排序的原始数组* @param left 左边有序序列的初始索引* @param mid 中间索引* @param right 右边索引* @param temp 做中转的数组*/public static void Merge(int []arr,int left,int mid,int right,int []temp) {int i = left;// 初始化 i, 左边有序序列的初始索引int j = mid+1;//初始化 j, 右边有序序列的初始索引int t = 0; //指向 temp 数组的当前索引//(1) 首先将左右两边依据规则移入到temp数组中//直到左右两边的一组序列处理完毕即可while(i<=mid&&j<=right) {if(arr[i]<=arr[j]) {//将两个中的最小值进行移入temptemp[t] = arr[i];//并且t、i的下标后移t++;i++;}else{temp[t] = arr[j];t++;j++;}}//(二) 将左右一边剩余的数据移入到temp中while(i<=mid) { //左边的剩余有序序列移到temp中temp[t] = arr[i];t++;i++;}while(j<=right) { //左边的剩余有序序列移到temp中temp[t] = arr[j];t++;j++;}//(三) 将temp的数组元素拷贝到arr数组中t = 0;int tempLeft = left;while(tempLeft<=right) {arr[tempLeft] = temp[t];tempLeft++;t++;}}}
测试代码:
package sortExer;import java.util.Arrays;public class MergeSort {public static void main(String[] args) {// int arr[]={8,4,5,7,1,3,6,2};// int temp[] = new int[arr.length];// System.out.println("排序前:"+Arrays.toString(arr));// mergeSort(arr, 0, arr.length-1, temp);// System.out.println("排序后:"+Arrays.toString(arr));int[] arr = new int[8000000];int temp[] = new int[arr.length];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 8000000);}long begin = System.currentTimeMillis();//System.out.println("排序前:"+Arrays.toString(arr));mergeSort(arr, 0, arr.length-1, temp);long end = System.currentTimeMillis();//System.out.println("排序后数组:"+Arrays.toString(arr));System.out.println("花费时间为:"+(double)(end-begin)/1000+"秒");}}
总结说明
这里的时间复杂度为O(n*log2^n),使用到了递归,采用了分治的方法
七、基数排序(桶排序进阶)
1、基数排序(桶排序)介绍

2、基数排序基本思想
说明:就是将数组中的数据放置在各个桶中,每一位为一轮,从个位开始,个位十位百位,每一轮放置到桶中之后,还要从桶中依次取出放置回原来的数组。轮数依据数组中的最大数决定。

3、基数排序图文说明
下面这组最大数就是三位数,所以总共轮数为三轮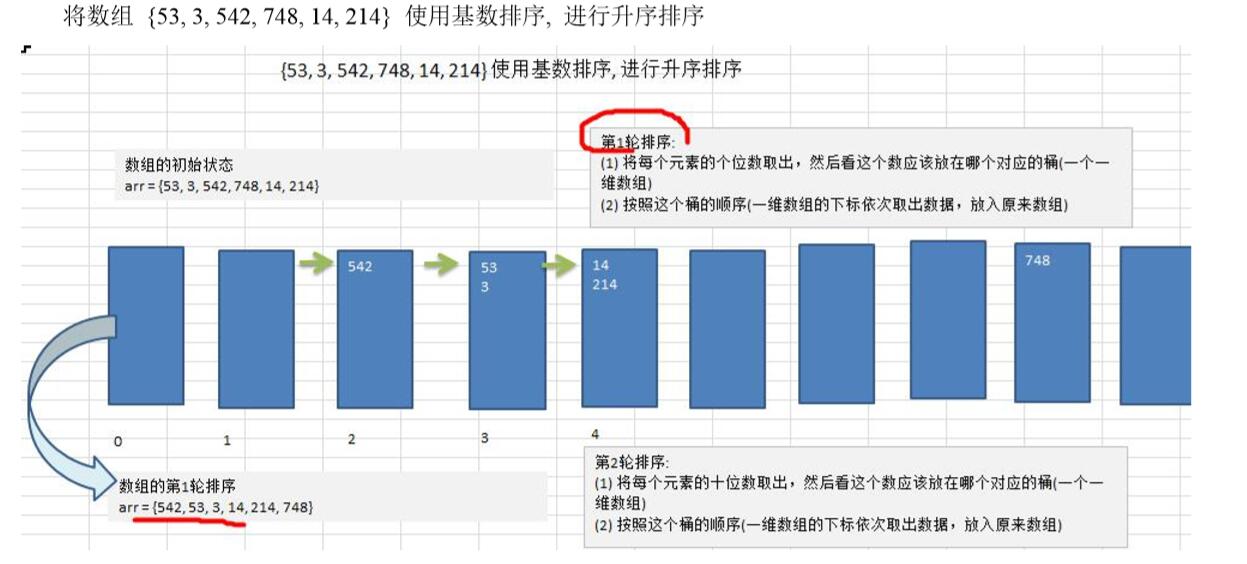
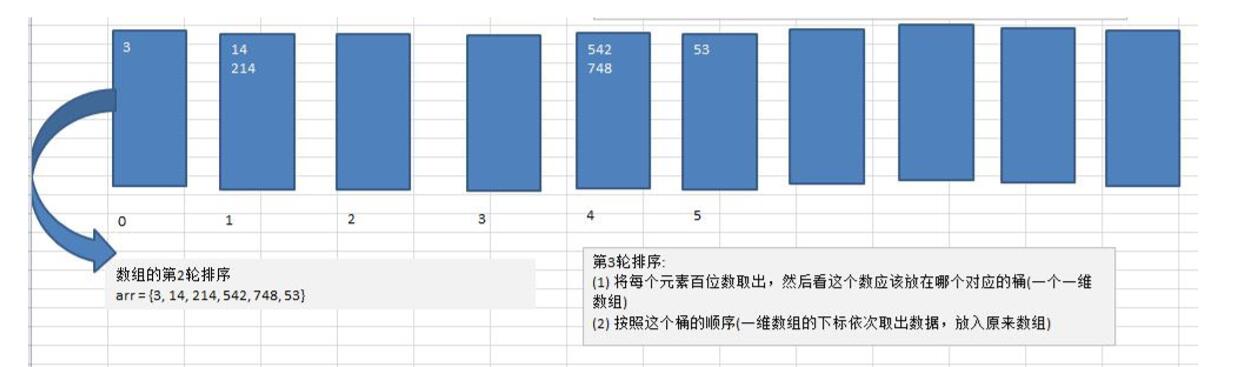
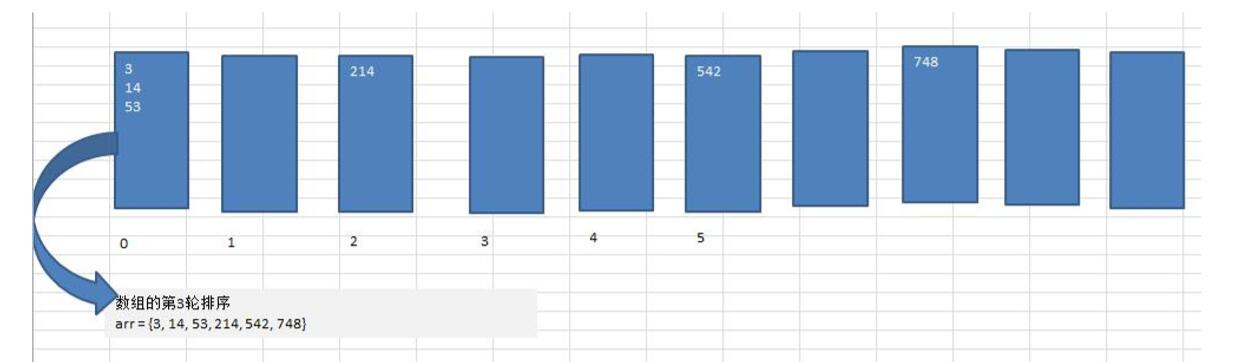
4、基数排序代码实现
说明:这里有三个大步骤分别为
① 找到arr数组中最大的数,并求出其长度(这里巧妙转为字符串求长度)
② 根据最大数长度来求出循环轮数,用一个二维数组作为桶,并用一个一维数组来为桶的0-10计数
③ 循环轮数中两个步骤,一个是依据其对应位数将数组中值依次放入桶中,另一个步骤是将放置到桶中的数据依照桶的顺序放置到原来数组arr中
package sortExer;import java.util.Arrays;public class CardinalSort {//基数排序,暂时只能解决正数的排序,且arr数组不能超过8千万个数据,否则报异常public static void cardinalSort(int[] arr) {if(arr.length == 0 || arr.length==1 ||arr == null) {return;}//1 找出arr数组中最大的数int max = arr[0];for(int i=1;i<arr.length;i++) {if(arr[i]>max) {max = arr[i];}}//算出max的位数,这里很巧妙,转换为String求lengthint maxLength = (max+"").length();//创建一个二维数组作为桶int[][] bucketArr = new int[10][arr.length];//这里每行的长度暂时设置为arr的数组长度int[] bucketCount = new int[10];//这个一维数组用来计数int div = 1;//等会作为除数//2 根据最大数的maxLength位数来进行maxLength次循环for(int n=1;n<=maxLength;n++,div*=10) {//这里div会一次*10增加//3 循环一维数组arr,首先从个位开始依次放入到桶中for(int i=0;i<arr.length;i++) {int intdigitOfElement = (int) (arr[i]/div%10);//获取到每个数的个位或十位,按照顺序获取bucketArr[intdigitOfElement][bucketCount[intdigitOfElement]] = arr[i];//依据对应位来将数存放到桶中bucketCount[intdigitOfElement]++;//记录桶中的长度也应该增加}int index = 0;//这里重写给arr赋值//4 遍历桶中的计数,将桶中的数据依次存放到arr数组中for(int i=0;i<bucketCount.length;i++) {//如果桶计数数组对应不为0if(bucketCount[i] != 0) {//那么将对应桶中的数据进行遍历到arr数组中for(int j=0;j<bucketCount[i];j++) {arr[index++] = bucketArr[i][j];//重复赋值到arr数组中}}//将桶中数据清空bucketCount[i] = 0;}//System.out.println("第"+ n +"次桶排序遍历结果为:"+Arrays.toString(arr));}System.out.println("基数排序已完成");}}
测试代码:
package sortExer;import java.util.Arrays;public class CardinalSort {public static void main(String[] args) {// int[] arr = {53,3,542,748,14,214};// cardinalSort(arr);int[] arr = new int[80000000];int temp[] = new int[arr.length];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * 80000000);}long begin = System.currentTimeMillis();//System.out.println("排序前:"+Arrays.toString(arr));cardinalSort(arr);long end = System.currentTimeMillis();//ystem.out.println("排序后数组:"+Arrays.toString(arr));System.out.println("花费时间为:"+(double)(end-begin)/1000+"秒");}}
运行结果:
这是第一组数据的测试情况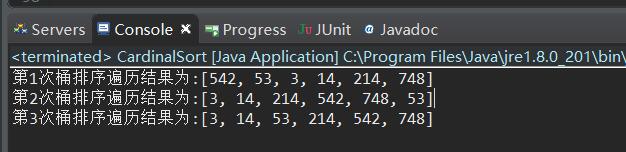
总结说明
基数排序相当于桶排序进阶,以空间换时间,效率甚至比快速排序还快,但是对应数据量过大就会抛出异常。
这里如果使用八千万数据放置到arr数组中,会java.lang.OutOfMemoryError: Java heap space的异常,内存溢出
计算方式:80000000114/1024/1024/1024=3G
11个数组存放八千万数据,每个int为4个字节:相乘为字节
字节(B)->KB->MB->G 都是1024换算单位
**
常用排序算法总结和对比
1、一张排序算法的比较图
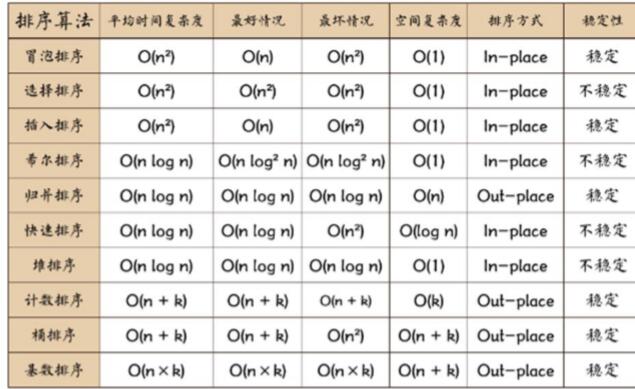
2、相关术语解释说明

整理者:长路 时间:2020/8/14-2020/8/21

