一、递归的介绍

1、递归应用场景

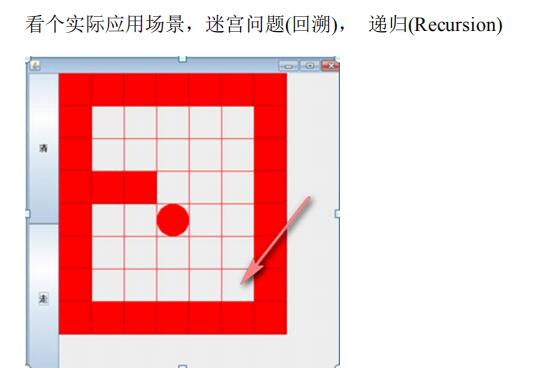
QQ截图20200812100845.jpg

2、递归的概念

QQ截图20200812100903.jpg

3、递归调用机制(案例+图示)


案例介绍

QQ截图20200812100957.jpg

  1. package com.mjj.test;
  3. public class UsualExer {
  4.     //打印问题
  5.     public static void test(int n) {
  6.         if(n>2) {
  7.             test(n-1);
  8.         }
  9.         System.out.println("n = "+n);
  10.     }
  12.     //阶乘问题
  13.     public static int factorial(int n) {
  14.         if(n==1) {
  15.             return 1;
  16.         }
  17.         return factorial(n-1)*n;
  18.     }
  20.     public static void main(String[] args) {
  22.         //测试打印问题
  23.         System.out.println("测试打印问题：");
  24.         test(4);
  25.         System.out.println();
  27.         //测试阶乘问题   1*2*3*4=24
  28.         System.out.println("4的阶乘处理结果为："+factorial(4));
  30.     }
  31. }

运行结果：
QQ截图20200812102107.jpg

图解说明

函数调用使用到的机制是栈，每次先执行栈顶的事件。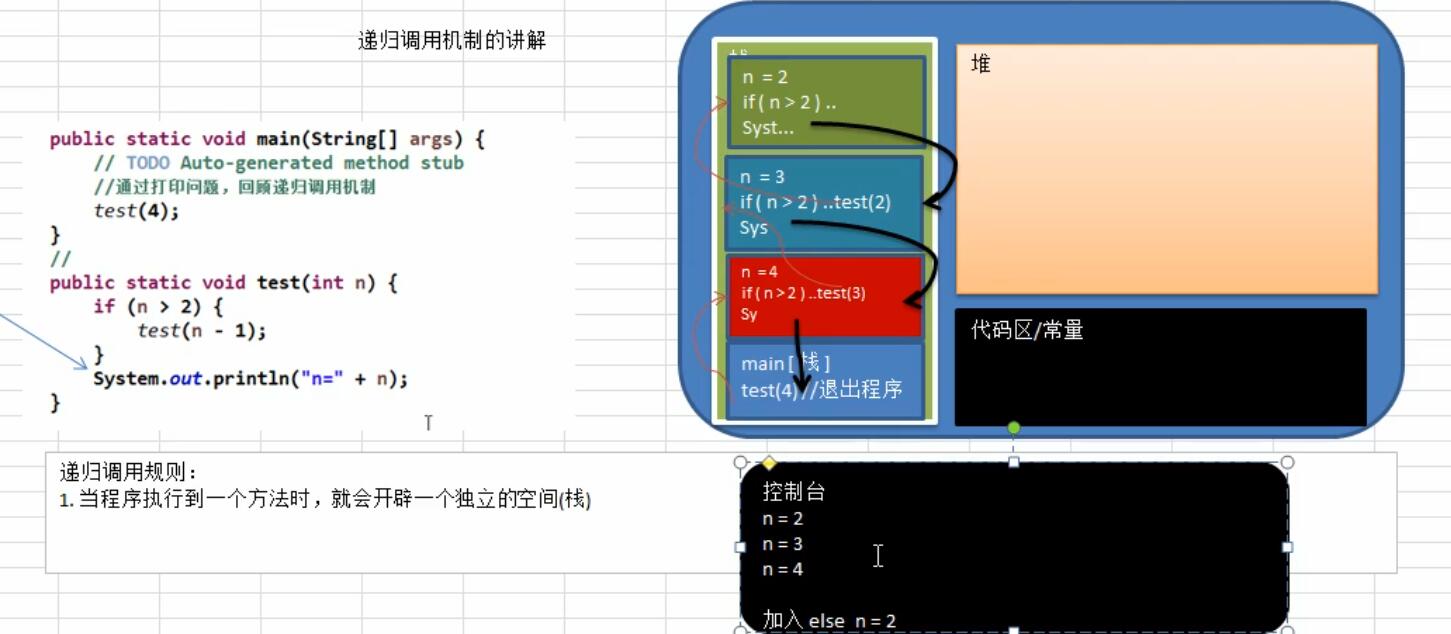
QQ截图20200812100334.jpg

4、递归能解决什么样的问题

QQ截图20200812103318.jpg

5、递归需要遵守的重要规则

QQ截图20200812103407.jpg

二、递归-迷宫问题

源代码：MazeExer.java

题目说明

有8行7列的二维数组，中间绿色的是围墙，从(1,1)开始，终点为(6,5)，在对应走的路径上设置为2表示走通。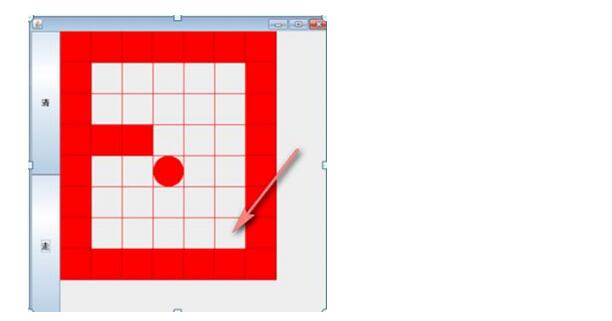
QQ截图20200812122323.jpg

代码演示

说明：走到(6,5)位置即为走通迷宫，对应数组位置上坐标0代表没走过，1代表是围墙，2代表走过，3表示已走过没有路

  1. package Recursion;
  3. public class MazeExer {
  5.     //将二维数组打印
  6.     public static void printArr(int arr[][]) {
  7.         for(int i=0;i<arr.length;i++) {
  8.             for(int j=0;j<arr[i].length;j++) {
  9.                 System.out.print(arr[i][j]+" ");
  10.             }
  11.             System.out.println();
  12.         }
  13.     }
  15.     //进行迷宫
  16.     /**
  17.      * 
  18.      * @Description
  19.      * @auther changlu
  20.      * @date Aug 12, 202011:55:22 AM
  21.      * @param arr 使用二维数组作为迷宫
  22.      * @param i  是当前位置的y轴
  23.      * @param j  是当前位置的x轴
  24.      * @return 返回true或false 代表该路是否可以走通
  25.      */
  26.     public static boolean setWay(int arr[][],int i,int j) {
  27.         //坐标0代表没走过，1代表是围墙，2代表走过，3表示已走过没有路
  28.         //设置(1,1)起点，(6,5)为终点
  29.         if(arr[6][5] == 2) {
  30.             return true;
  31.         }else {
  32.             //当前位置为0时
  33.             if(arr[i][j] == 0) {
  34.                 arr[i][j] = 2;//表示已经走过
  35.                 //可以往4个方向走
  36.                 if(setWay(arr, i+1, j)) {//这里往下走
  37.                     return true;
  38.                 }else if(setWay(arr, i, j+1)) {//这里往右走
  39.                     return true;
  40.                 }else if(setWay(arr, i-1, j)) {//往上走
  41.                     return true;
  42.                 }else if(setWay(arr, i, j-1)) {//往左走
  43.                     return true;
  44.                 }else {
  45.                     //上下左右路都走不通
  46.                     arr[i][j] = 3;//标识这里已经走过并且走不通
  47.                     return false;
  48.                 }
  49.             }else {
  50.                 //当前位置上为1,2,3 就都不走
  51.                 return false;
  52.             }
  53.         }
  54.     }
  55. }

测试：

  1. public class MazeExer {    
  2.     public static void main(String[] args) {
  3.         //创建一个8行7列的迷宫
  4.         int[][] arr = new int[8][7];
  5.         //给迷宫外围一圈赋值围墙
  6.         for(int i=0;i<=6;i++) {
  7.             arr[0][i] = 1;
  8.             arr[7][i] = 1;
  9.         }
  11.         for(int i=0;i<=7;i++) {
  12.             arr[i][0] = 1;
  13.             arr[i][6] = 1;
  14.         }
  15.         //额外作墙板
  16.         arr[3][1] = 1;
  17.         arr[3][2] = 1;
  19.         //第一次打印
  20.         printArr(arr);
  22.         boolean flag = setWay(arr, 1, 1);
  23.         System.out.println("是否能走通："+flag);
  25.         //打印迷宫
  26.         System.out.println("\n走通后的迷宫:");
  27.         printArr(arr);
  29.     }
  30. }

运行结果:
QQ截图20200812122753.jpg

三、递归-八皇后问题(回溯算法)

1、八皇后问题介绍

QQ截图20200813100315.jpgQQ截图20200813100328.jpg

2、八皇后问题算法思路分析

QQ截图20200813100418.jpgQQ截图20200813100426.jpg

代码演示(说明)

属性说明：这里棋盘是否一个一维数组来进行代替，如arr[0] = 2，这个下标0代表是第一行，2代表的是这行上的第三个，使用count来计算方法的总数。下标为行数，值为行中的位置。

方法说明：这里总共 三个方法，打印数组、检查对应行与之前的棋盘有同列以及同斜线的、递归回溯求解一维数组。
printArr()：使用Arrays打印数组
check(int n) ：传入下标，通过一维数组来查看是否不符合同列以及同斜线情况，符合返回true，不符合返回false
getQueue8(int n)：通过递归来对棋盘上所有情况进行检查选择，中途会使用check()进行检查

时间复杂度为：8^8,整体算法会有回溯，从而暴力解决获取所有情况。

  1. package StackExer;
  3. import java.util.Arrays;
  5. public class Queue8 {
  6.     //使用一维数组来代替八皇后棋盘
  7.     //下标为第几行，对应的值这一行的第几个
  8.     private int max = 8;
  9.     private int [] array = new int[8];
  10.     private static int count;
  12.     //进行八皇后棋盘获取，n为行
  13.     public void getQueue8(int n) {
  14.         //如果n为8说明，已经成功获取八皇后棋盘摆棋方式
  15.         if(n == max) {
  16.             printArr();
  17.             return;
  18.         }
  20.         //进行遍历
  21.         for(int i=0;i<max;i++) {
  22.             //填充第n列上的值为i，i代表第几个位置
  23.             array[n] = i;
  24.             //判断是否有出现冲突的情况
  25.             if(check(n)) {
  26.                 //没有冲突情况进行递归
  27.                 getQueue8(n+1);
  28.             }
  30.         }
  31.     }
  34.     //创建一个检查方法,传入的n是第几行
  35.     public boolean check(int n) {
  36.         //判断是否存在同一列以及同一斜线的
  37.         for(int i=0;i<n;i++) {
  38.             if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[i]-array[n])) {
  39.                 return false;
  40.             }
  41.         }
  42.         //没有同一列以及同一斜线的返回true
  43.         return true;
  44.     }
  47.     //用来打印一维数组
  48.     public void printArr() {
  49.         count++;
  50.         System.out.println(Arrays.toString(array));
  51.     }
  54. }

测试方法：

  1. public class Queue8 {    
  2.     public static void main(String[] args) {
  3.         Queue8 queue8 = new Queue8();
  4.         queue8.getQueue8(0);
  5.         System.out.printf("摆棋方式有%d种",count);
  6.     }
  7. }

运行结果：
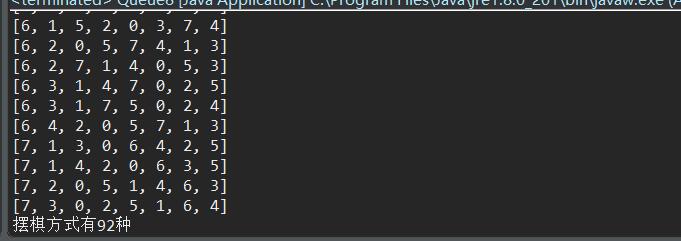
QQ截图20200813121232.jpg

四、全排列

参考文章：轻松理解全排列算法的递归解法
**

详细过程(二部分)


① 入门，并不是求解全排列，而是列举四种全排列形式

image.png

  1. public class Main {
  2.     public static void main(String[] args) {
  3.         int[] a = {1,2,3,4};
  4.         quanpailie(a,0,a.length);
  6.     }
  8.     private static void quanpailie(int[] a, int cur, int length) {
  9.         for(int i = cur;i<length;i++){
  10.             swap(a, cur,i );
  11.             System.out.println(Arrays.toString(a));
  12.             swap(a, i, cur);//将先前替换的撤销
  13.         }
  14.     }
  16.     public static void swap(int[]a,int cur,int i){
  17.         int temp = a[cur];
  18.         a[cur] = a[i];
  19.         a[i] = temp;
  20.     }
  22. }

运行结果：
image.png

② 使用递归求解全排列

添加出口条件，来进行输出

  1. package exer;
  2. import java.util.*;
  5. public class Main {
  6.     public static void main(String[] args) {
  7.         int[] a = {1,2,3,4};
  8.         quanpailie(a,0,a.length);
  10.     }
  12.     //进行全排列
  13.     private static void quanpailie(int[] a, int cur, int length) {
  14.         //输出列举的情况
  15.         if(cur == length){
  16.             System.out.println(Arrays.toString(a));
  17.         }
  19.         for(int i = cur;i<length;i++){
  20.             swap(a, cur,i );
  21.             //System.out.println(Arrays.toString(a));
  22.             quanpailie(a, cur+1, length);//分解为子问题进行递归
  23.             swap(a, i, cur);
  24.         }
  25.     }
  27.     //替换操作
  28.     public static void swap(int[]a,int cur,int i){
  29.         int temp = a[cur];
  30.         a[cur] = a[i];
  31.         a[i] = temp;
  32.     }
  33. }

image.png 包含24种情况

—————————————————————————————————————————————————————————————
**

解决全排列重复问题(忽略重复的全排列)

对于全排列如果我们不想要重复的排列数据时，如下数组中包含重复的元素：
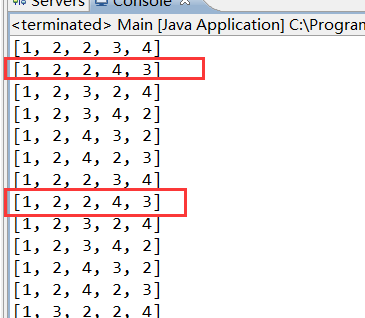image.pngimage.png 会出现重复的情况
**

添加一个查询方法：
cur是数组当前从cur位置开始，i是对应要调换的数，我们只需要判断在[cur,i)之间是否与在数组中i位置的数据相同，那么我们就返回false

  1. //判断是否出现重复的情况
  2. public static boolean isRepeat(int[] b,int cur,int i){
  3.     //因为我们是要将cur与i来进行调换，如果之前重复的话就不需要进行往下递归来生成对应值
  4.     for(int j=cur;j<i;j++){
  5.         if(b[j] == b[i])
  6.             return false;
  7.     }
  8.     return true;
  9. }

完整如下：

  1. public class Main {
  2.     public static void main(String[] args) {
  3.         int[] a = {1,2,2,3,4};
  4.         quanpailie(a,0,a.length);
  6.     }
  8.     //进行全排列
  9.     private static void quanpailie(int[] a, int cur, int length) {
  10.         //输出列举的情况
  11.         if(cur == length){
  12.             System.out.println(Arrays.toString(a));
  13.         }
  15.         for(int i = cur;i<length;i++){
  16.             //判断是否与之前的有重复元素的情况
  17.             if(!isRepeat(a, cur, i))
  18.                 return;
  19.             swap(a, cur,i );
  20.             //System.out.println(Arrays.toString(a));
  21.             quanpailie(a, cur+1, length);//分解为子问题进行递归
  22.             swap(a, i, cur);
  23.         }
  24.     }
  26.     //替换操作
  27.     public static void swap(int[]a,int cur,int i){
  28.         int temp = a[cur];
  29.         a[cur] = a[i];
  30.         a[i] = temp;
  31.     }
  33.     //判断是否出现重复的情况
  34.     public static boolean isRepeat(int[] a,int cur,int i){
  35.         //因为我们是要将cur与i来进行调换，如果之前重复的话就不需要进行往下递归来生成对应值
  36.         for(int j=cur;j<i;j++){
  37.             if(a[j] == a[i])
  38.                 return false;
  39.         }
  40.         return true;
  41.     }
  44. }

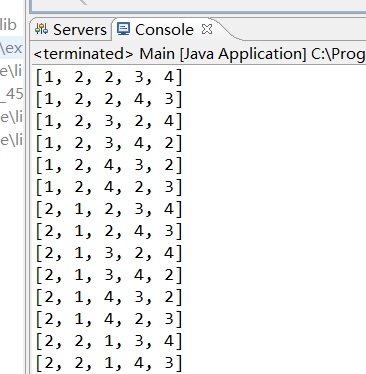image.png 就没有重复情况了

整理者：长路 时间：2020/8/12、2020/11/13