一、二叉树

1、为什么需要树这种数据结构(数组、链表、树说明)

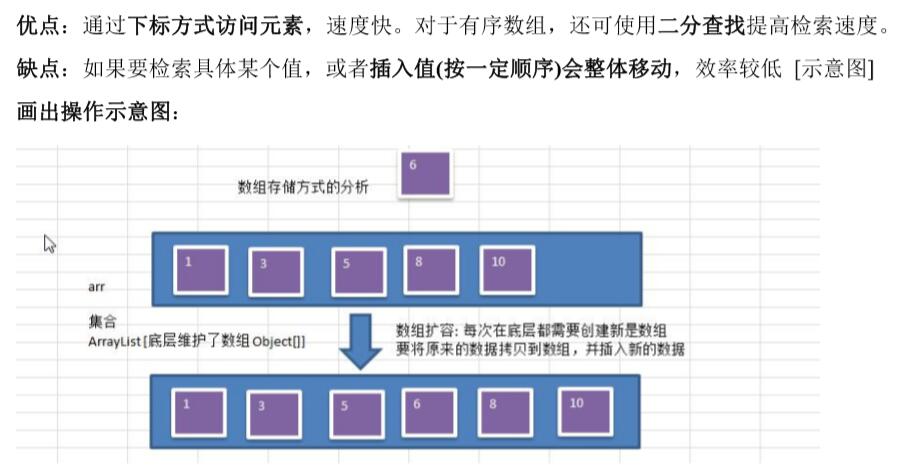
1) 数组存储方式的分析(缺点插入)

QQ截图20200826093424.jpg

2) 链式存储方式的分析(缺点检索)

QQ截图20200826093508.jpgQQ截图20200826093515.jpg

3) 树存储方式的分析(提高存储读取)

QQ截图20200826093558.jpg

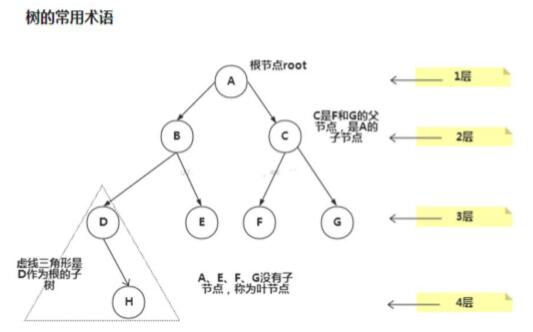
2、树示意图(常用术语)

QQ截图20200826094521.jpgQQ截图20200826094527.jpg

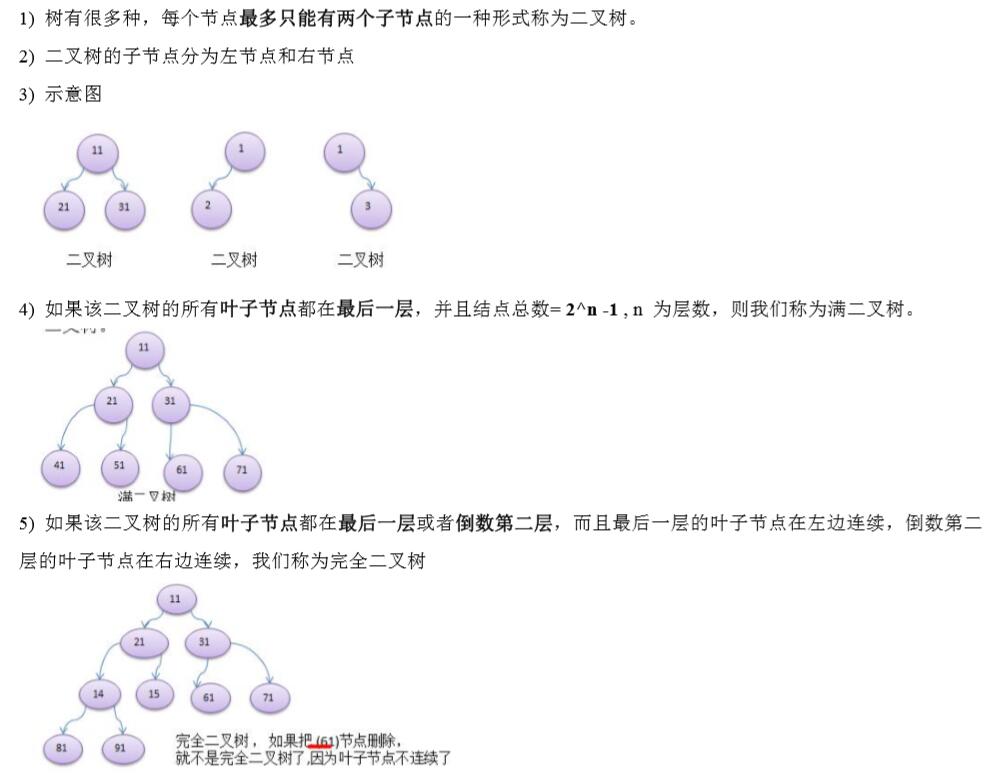
3、二叉树的概念(包含满二叉树及完全二叉树)

说明：二叉树的介绍以及满二叉树和完全二叉树的介绍

QQ截图20200826094652.jpg、

4、二叉树遍历应用实例(前序,中序,后序)

源代码：BinaryTree.java

思路分析

注意的是这里的方法增加于上面的类中进行实现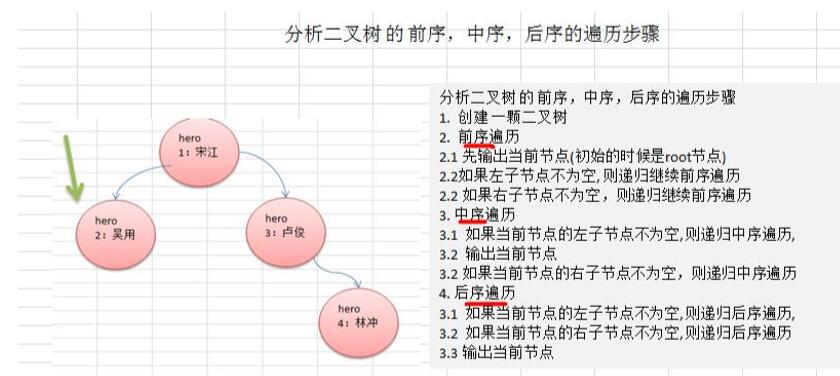
QQ截图20200826100308.jpg

代码实现(完整过程+测试)

源代码：BinaryTree.java

说明：分为两个类，一个为二叉树节点类包含前中后序遍历，另一个是二叉树类包含根节点以及进行前中后序的调用方法。
**

节点类

  1. //树的节点
  2. class TreeNode{
  3.     private String name;
  4.     private int id;
  5.     private TreeNode left;
  6.     private TreeNode right;
  7.     public TreeNode(String name, int id) {
  8.         super();
  9.         this.name = name;
  10.         this.id = id;
  11.     }
  13.     //前序遍历
  14.     public void preOrder() {
  15.         System.out.println(this);
  16.         //如果左节点不为空那么向左递归
  17.         if(this.left != null) {
  18.             this.left.preOrder();
  19.         }
  20.         //右节点不为空进行向右递归
  21.         if(this.right != null) {
  22.             this.right.preOrder();
  23.         }
  24.     }
  26.     //中序遍历
  27.     public void infixOrder() {
  28.         // 如果左节点不为空那么向左递归
  29.         if (this.left != null) {
  30.             this.left.infixOrder();
  31.         }
  32.         System.out.println(this);
  33.         // 右节点不为空进行向右递归
  34.         if (this.right != null) {
  35.             this.right.infixOrder();
  36.         }
  37.     }
  39.     //后序遍历
  40.     public void postOrder() {
  41.         // 如果左节点不为空那么向左递归
  42.         if (this.left != null) {
  43.             this.left.postOrder();
  44.         }
  45.         // 右节点不为空进行向右递归
  46.         if (this.right != null) {
  47.             this.right.postOrder();
  48.         }
  49.         System.out.println(this);
  50.     }
  52.     public void setName(String name) {
  53.         this.name = name;
  54.     }
  55.     public void setId(int id) {
  56.         this.id = id;
  57.     }
  58.     public void setLeft(TreeNode left) {
  59.         this.left = left;
  60.     }
  61.     public void setRight(TreeNode right) {
  62.         this.right = right;
  63.     }
  65.     @Override
  66.     public String toString() {
  67.         return "TreeNode [name=" + name + ", id=" + id + "]";
  68.     }
  69. }

二叉树类

  1. //二叉树
  2. class MyBinaryTree{
  3.     //设置一个根节点
  4.     private TreeNode root;
  6.     public void setRoot(TreeNode root) {
  7.         this.root = root;
  8.     }
  10.     //前序遍历
  11.     public void preOrder() {
  12.         //判断根节点是否为空
  13.         if(root != null) {
  14.             root.preOrder();//进行前序遍历
  15.         }else {
  16.             System.out.println("根节点为空无法前序遍历!");
  17.         }
  18.     }
  20.     // 中序遍历
  21.     public void infixOrder() {
  22.         if (root != null) {
  23.             root.infixOrder();// 进行中序遍历
  24.         }else {
  25.             System.out.println("根节点为空无法中序遍历!");
  26.         }
  27.     }
  29.     // 后序遍历
  30.     public void postOrder() {
  31.         if (root != null) {
  32.             root.postOrder();// 进行后序遍历
  33.         }else {
  34.             System.out.println("根节点为空无法后序遍历!");
  35.         }
  36.     }
  38. }

测试类

  1. package tree;
  3. public class BinaryTree {
  4.     public static void main(String[] args) {
  5.         //创建一个二叉树
  6.         MyBinaryTree tree = new MyBinaryTree();
  7.         //创建四个节点
  8.         TreeNode root = new TreeNode("宋江", 1);
  9.         TreeNode node2 = new TreeNode("吴用", 2);
  10.         TreeNode node3 = new TreeNode("卢俊", 3);
  11.         TreeNode node4 = new TreeNode("林冲", 4);
  13.         //将node节点存放到root中
  14.         root.setLeft(node2);
  15.         root.setRight(node3);
  16.         node3.setRight(node4);
  17.         //将root存放到二叉树中
  18.         tree.setRoot(root);
  20.         //进行前序遍历    
  21.         System.out.println("前序遍历：");
  22.         tree.preOrder();
  24.         System.out.println("中序遍历：");
  25.         tree.infixOrder();
  27.         System.out.println("后序遍历：");
  28.         tree.postOrder();
  29.     }
  30. }

运行结果：
QQ截图20200826105426.jpg
**

小测试

说说下图的前中后遍历的结果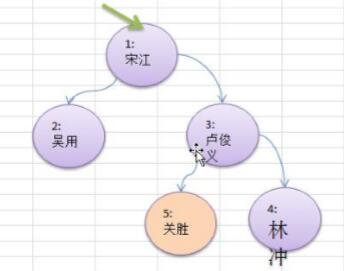
QQ截图20200826105546.jpg
前序：12354
中序：21534
后序：25431
**

5、查找指定节点(前中后序)

思路分析

与之前前后序遍历几乎相同，只不过这里面增加的返回值以及比较判断的过程。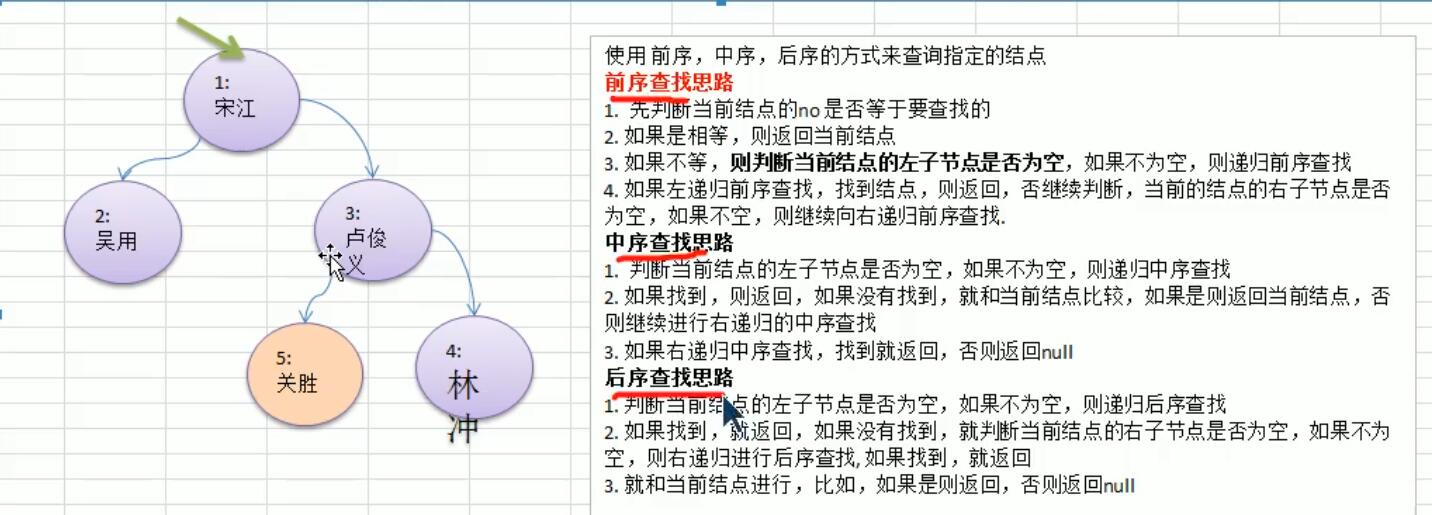
QQ截图20200827104826.jpg

代码实现

说明：对于节点类以及二叉树类都会有前中后序的方法实现
**

节点类

说明：可以看到每种查找几乎都只是顺序变了而已，其中对于查找到的值使用resultNode来接收并根据实际情况返回，并且在判断比较id时才是真正开始比较，这里输出来体现。

  1.     //前序遍历查找
  2.     public TreeNode preOrderSearch(int findId) {
  3.         System.out.println("前序比较~");
  4.         if(this.id == findId) {
  5.             return this;
  6.         }
  7.         //进行向左子树进行查找
  8.         TreeNode resultNode = null;
  9.         if(this.left != null) {
  10.             resultNode = this.left.preOrderSearch(findId);//向左进行查找返回
  11.         }
  12.         if(resultNode != null) {
  13.             return resultNode;
  14.         }
  15.         //向右子树进行查找
  16.         if(this.right != null) {
  17.             resultNode = this.right.preOrderSearch(findId);//向右查找返回
  18.         }
  19.         return resultNode;//返回对应查找到的值
  20.     }
  22.     //中序遍历查找
  23.     public TreeNode infixOrderSearch(int findId) {
  24.         // 首先进行向左子树进行查找
  25.         TreeNode resultNode = null;
  26.         if (this.left != null) {
  27.             resultNode = this.left.infixOrderSearch(findId);// 向左进行查找返回
  28.         }
  29.         if(resultNode != null) {
  30.             return resultNode;
  31.         }
  32.         System.out.println("中序比较~");
  33.         if(this.id == findId) {
  34.             return this;
  35.         }
  37.         //向右子树进行查找
  38.         if(this.right != null) {
  39.             resultNode = this.right.infixOrderSearch(findId);//向右查找返回
  40.         }
  41.         return resultNode;//返回对应查找到的值
  42.     }
  44.     //后序遍历查找
  45.     public TreeNode postOrderSearch(int findId) {
  46.         // 首先进行向左子树进行查找
  47.         TreeNode resultNode = null;
  48.         if (this.left != null) {
  49.             resultNode = this.left.infixOrderSearch(findId);// 向左进行查找返回
  50.         }
  51.         if(resultNode != null) {
  52.             return resultNode;
  53.         }
  54.         //向右子树进行查找
  55.         if (this.right != null) {
  56.             resultNode = this.right.infixOrderSearch(findId);// 向右查找返回
  57.         }
  58.         if(resultNode != null) {
  59.             return resultNode;
  60.         }
  62.         System.out.println("后序比较~");
  63.         if(this.id == findId) {
  64.             return this;//进行判断值进行查找
  65.         }
  66.         return resultNode;
  67.     }

二叉树类

说明：这里只是简单的判断根节点是否为空之后就对根节点进行对应的查找方法调用

  1.     //前序遍历查找
  2.     public TreeNode preOrderSearch(int findId) {
  3.         if(root != null) {
  4.             return root.preOrderSearch(findId);
  5.         }else {
  6.             System.out.println("二叉树为空无法查找!");
  7.             return null;
  8.         }
  9.     }
  11.     // 中序遍历查找
  12.     public TreeNode infixOrderSearch(int findId) {
  13.         if (root != null) {
  14.             return root.infixOrderSearch(findId);
  15.         } else {
  16.             System.out.println("二叉树为空无法查找!");
  17.             return null;
  18.         }
  19.     }
  21.     // 后序遍历查找
  22.     public TreeNode postOrderSearch(int findId) {
  23.         if (root != null) {
  24.             return root.postOrderSearch(findId);
  25.         } else {
  26.             System.out.println("二叉树为空无法查找!");
  27.             return null;
  28.         }
  29.     }

测试类

  1. package tree;
  3. public class BinaryTree {
  4.     public static void main(String[] args) {
  5.         //创建一个二叉树
  6.         MyBinaryTree tree = new MyBinaryTree();
  7.         //创建四个节点
  8.         TreeNode root = new TreeNode("宋江", 1);
  9.         TreeNode node2 = new TreeNode("吴用", 2);
  10.         TreeNode node3 = new TreeNode("卢俊", 3);
  11.         TreeNode node4 = new TreeNode("林冲", 4);
  12.         TreeNode node5 = new TreeNode("关胜", 5);
  14.         //将node节点存放到root中
  15.         root.setLeft(node2);
  16.         root.setRight(node3);
  17.         node3.setRight(node4);
  18.         node3.setLeft(node5);
  19.         //将root存放到二叉树中
  20.         tree.setRoot(root);
  22.         //进行前序遍历    
  23.         System.out.println("前序遍历：");
  24.         tree.preOrder();
  26.         System.out.println("中序遍历：");
  27.         tree.infixOrder();
  29.         System.out.println("后序遍历：");
  30.         tree.postOrder();
  31.         System.out.println("------------------------");
  33.         //开始前中后序遍历查找
  34.         System.out.println("前序遍历查找：");
  35.         TreeNode node = tree.preOrderSearch(5);
  36.         if(node != null) {
  37.             System.out.println("找到节点为:"+node);            
  38.         }else {
  39.             System.out.println("未找到节点!");
  40.         }
  41.         System.out.println("------------------------");
  42.         //开始中序遍历查找
  43.         System.out.println("中序遍历查找：");
  44.         TreeNode node1 = tree.infixOrderSearch(5);
  45.         if (node1 != null) {
  46.             System.out.println("找到节点为:" + node1);
  47.         } else {
  48.             System.out.println("未找到节点!");
  49.         }
  50.         System.out.println("------------------------");
  51.         //开始中序遍历查找
  52.         System.out.println("后序遍历查找：");
  53.         TreeNode node6 = tree.postOrderSearch(5);
  54.         if (node6 != null) {
  55.             System.out.println("找到节点为:" + node6);
  56.         } else {
  57.             System.out.println("未找到节点!");
  58.         }
  59.     }
  60. }

运行结果
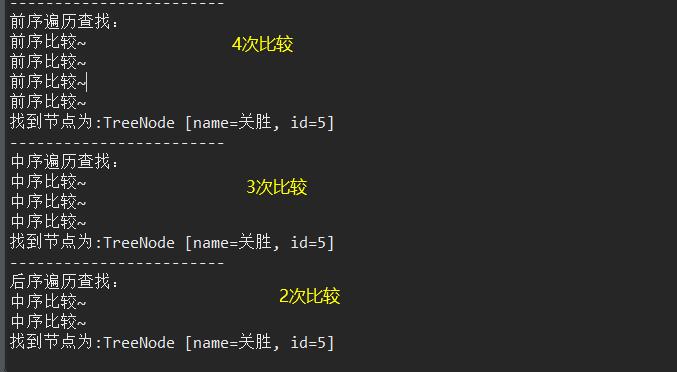
QQ截图20200827111725.jpg

6、删除节点

源代码：BinaryTree.java

思路分析

要求说明
1)如果删除的节点是叶子节点，则删除该节点
2) 如果删除的节点是非叶子节点，则删除该子树.
3) 测试，删除掉 5 号叶子节点 和 3 号子树.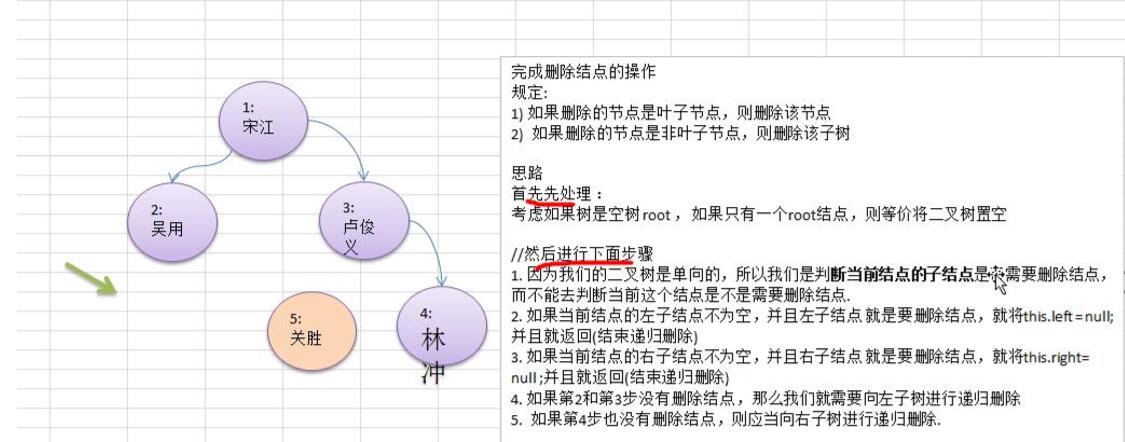
QQ截图20200828100653.jpg

代码实现(完整过程+测试)

说明：节点类以及二叉树类都只有各自一个删除方法，二叉树用于处理root根节点的情况，节点类处理左右两边情况

节点类

  1. //删除节点操作
  2.     public void delNodeById(int delId) {
  3.         //首先是判断左子节点是否为空，并且左子节点的id是否为要查找的id，是的话就删除
  4.         if(this.left != null && this.left.id == delId) {
  5.             this.left = null;
  6.             System.out.println("成功删除节点,其id值为:"+delId);
  7.             return;//删除成功就结束
  8.         }
  9.         //首先是判断右子节点是否为空，并且右子节点的id是否为要查找的id，是的话就删除
  10.         if(this.right != null && this.right.id == delId) {
  11.             this.right = null;
  12.             System.out.println("成功删除节点,其id值为:"+delId);
  13.             return;//删除成功就结束
  14.         }
  16.         //运行到这里就说明该节点的左右孩子都不符合删除要求，那么进行递归操作
  17.         if(this.left != null) {
  18.             this.left.delNodeById(delId);
  19.         }
  20.         if(this.right != null) {
  21.             this.right.delNodeById(delId);
  22.         }
  25.     }

二叉树类

  1.     //删除指定id的节点
  2.     public void delNodeById(int delId) {
  3.         if(root != null) {
  4.             //来判断根节点是否为要删除的节点
  5.             if(root.getId() == delId) {
  6.                 root = null;
  7.             }else {
  8.                 //不为要删除的节点，那么执行删除节点的方法
  9.                 root.delNodeById(delId);
  10.             }
  11.         }else {
  12.             System.out.println("树为空，无法进行删除操作!");
  13.         }
  14.     }

测试类

  1. package tree;
  3. public class BinaryTree {
  4.     public static void main(String[] args) {
  5.         //创建一个二叉树
  6.         MyBinaryTree tree = new MyBinaryTree();
  7.         //创建四个节点
  8.         TreeNode root = new TreeNode("宋江", 1);
  9.         TreeNode node2 = new TreeNode("吴用", 2);
  10.         TreeNode node3 = new TreeNode("卢俊", 3);
  11.         TreeNode node4 = new TreeNode("林冲", 4);
  12.         TreeNode node5 = new TreeNode("关胜", 5);
  14.         //将node节点存放到root中
  15.         root.setLeft(node2);
  16.         root.setRight(node3);
  17.         node3.setRight(node4);
  18.         node3.setLeft(node5);
  19. //        //将root存放到二叉树中
  20.         tree.setRoot(root);
  21. //        
  22.         //进行前序遍历    
  23.         System.out.println("前序遍历：");
  24.         tree.preOrder();
  25.         System.out.println();
  26.         System.out.println("开始执行删除节点操作:");
  27.         tree.delNodeById(5);//执行删除操作
  28.         tree.delNodeById(3);//执行删除操作
  29.         System.out.println();
  30.         System.out.println("删除节点后前序遍历：");
  31.         tree.preOrder();
  32.     }

运行结果：
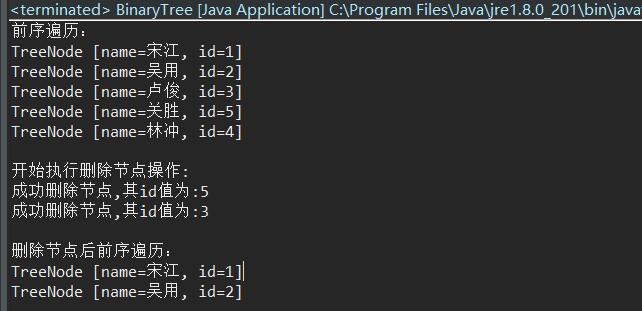
QQ截图20200828101532.jpg

二、顺序存储二叉树

1、顺序存储二叉树的概念

基本说明

从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组，
看右面的示意图：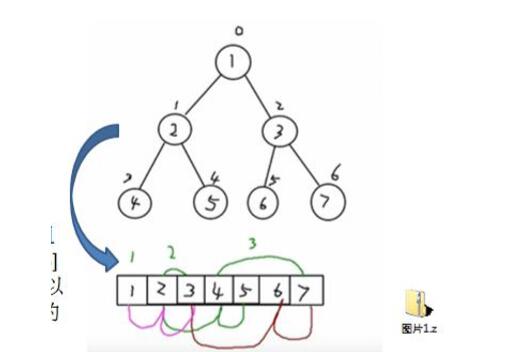
QQ截图20200828102459.jpg

要求:

1) 右图的二叉树的结点，要求以数组的方式来存放 arr:[1,2,3,4,5,6,6]
2) 要求在遍历数组 arr 时，仍然可以以前序遍历，中序遍历和后序遍历的方式完成结点的遍

特点说明

说明：对一个左子节点以及右子节点、父节点的方式计算可以根据上面示例图来进行查看
QQ截图20200828102539.jpg

2、代码实现

说明：这里使用的是前序遍历的方法

  1. package tree;
  3. public class ArrayBinaryTreeDemo {
  4.     public static void main(String[] args) {
  5.         int[] arr = {1,2,3,4,5,6,7};
  6.         ArrayBinaryTree tree = new ArrayBinaryTree(arr);
  7.         //开始进行前序遍历
  8.         tree.preOrder();
  10.     }
  11. }
  13. class ArrayBinaryTree{
  14.     private int[] arr;//用于存放数据节点的数据
  16.     public ArrayBinaryTree(int[] arr) {
  17.         super();
  18.         this.arr = arr;
  19.     }
  21.     //进行重载调用有参数的方法
  22.     public void preOrder() {
  23.         preOrder(0);
  24.     }
  26.     //进行前序遍历
  27.     public void preOrder(int index){ 
  28.         //不符合条件的输出
  29.         if(arr == null || arr.length == 0) {
  30.             System.out.println("数组为空，二叉树无法遍历");
  31.             return;
  32.         }
  33.         System.out.println(arr[index]);
  34.         //向左递归 对应节点是否存在
  35.         if((index*2+1)<arr.length) {
  36.             preOrder(index*2+1);
  37.         }
  39.         //向右递归
  40.         if((index*2+2)<arr.length) {
  41.             preOrder(index*2+2);
  42.         }
  44.     }
  45. }

前中后序遍历如下：
QQ截图20200902113431.jpg

运行结果：
QQ截图20200902113543.jpg

整理者：长路 时间：2020/8/26-2020/8/28