题目链接

题目描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：

输入: “cbbd”
输出: “bb”

暴力

  遍历每一个字串并记录最长的回文字串。另外，要注意c++的substr和java的substring的区别，在内循环的变量设计会有一点区别，substr的第二个参数是取字符的个数，而substring的第二个参数是截取结束端点的开区间。
  太暴力了，实际上是三循环(要判断回文)，果不其然测试用例47超时～

代码

  1. class Solution {
  2. public:
  3.     string longestPalindrome(string s) {
  4.         if(s.size() <= 1)
  5.             return s;
  7.         string result = "";
  8.         for(int i = 0; i < s.size(); i++){
  9.             for(int j = 1; j <= s.size() - i; j++){
  10.                 string temp = s.substr(i, j);
  11.                 if(helper(temp) && temp.size() > result.size())
  12.                     result = s.substr(i, j);
  13.             }
  14.         } 
  15.         return result;          
  16.     }
  18. private:
  19.     bool helper(string s){
  20.         int len = s.size();
  21.         for(int i = 0; i < len / 2; i++){
  22.             if(s[i] != s[len - 1 - i])
  23.                 return false;
  24.         }
  26.         return true;
  27.     }
  28. };

暴力版动态规划

  本人愚笨，仍然在DP的海洋里沉底～以下是学习leetcode评论区大佬们的题解而写的代码～
  题目关键在于如何写出状态转移方程，那本题什么是状态呢？一般情况下，题目问什么就设什么为状态，后续如果问题需要优化在迭代状态。所幸，本题的状态很好表示，就是判断当前子串是否为回文串。接下来就考虑状态转移过程，实际就是判断回文，因为回文包含着状态转移的思想。可以这么想，使用对撞指针由两端向中间递归判断：

  1. 当前两端点字符不相等，则肯定不是回文；
  2. 若相等，继续判断去除两端点的子串。如果子串是回文，则当前串为回文；若不是，当前串不是回文。

  我们发现当前串回文实际上是利用了当前串的子串的回文状态进行判断，这就包含了状态的转移。私以为，动态规划是从里向外解决问题，与我们日常思维方式不太一样，因为谁能一开始就看清事物的本质呢～大多都是自外向里，抽丝剥茧。而且，就我目前的学习理解，学好递归是理解动态规划的基础，这个想法正确与否，以后会在学习过程不断实践，加油～
  下面就是暴力版的四步骤：

  1. 定义状态：dp[i][j]表示当前子串s[i,j]是否回文
  2. 状态转移方程：dp[i][j] = s[i] == s[j] && dp[i + 1][j - 1]

    边界条件：
    [i + 1 , j - 1]为单个字符或者空时，肯定是回文
    所以考虑[i + 1 , j - 1]不构成区间时，即为边界条件。
    =》j - 1 - (i + 1) + 1 < 2，即j - i < 3

  1. 初始化状态：从状态方程的边界条件出发思考如何初始化，显然将单个字符初始化为true，即dp[i][i] == true
  2. 输出方式：记录子串起始start和长度即可。

  注意：一定要先得到小子串的状态，才能判断大子串的状态。下面代码采用的是定右边界，从小到大枚举左边界。

  画一个dp表格，加深理解～
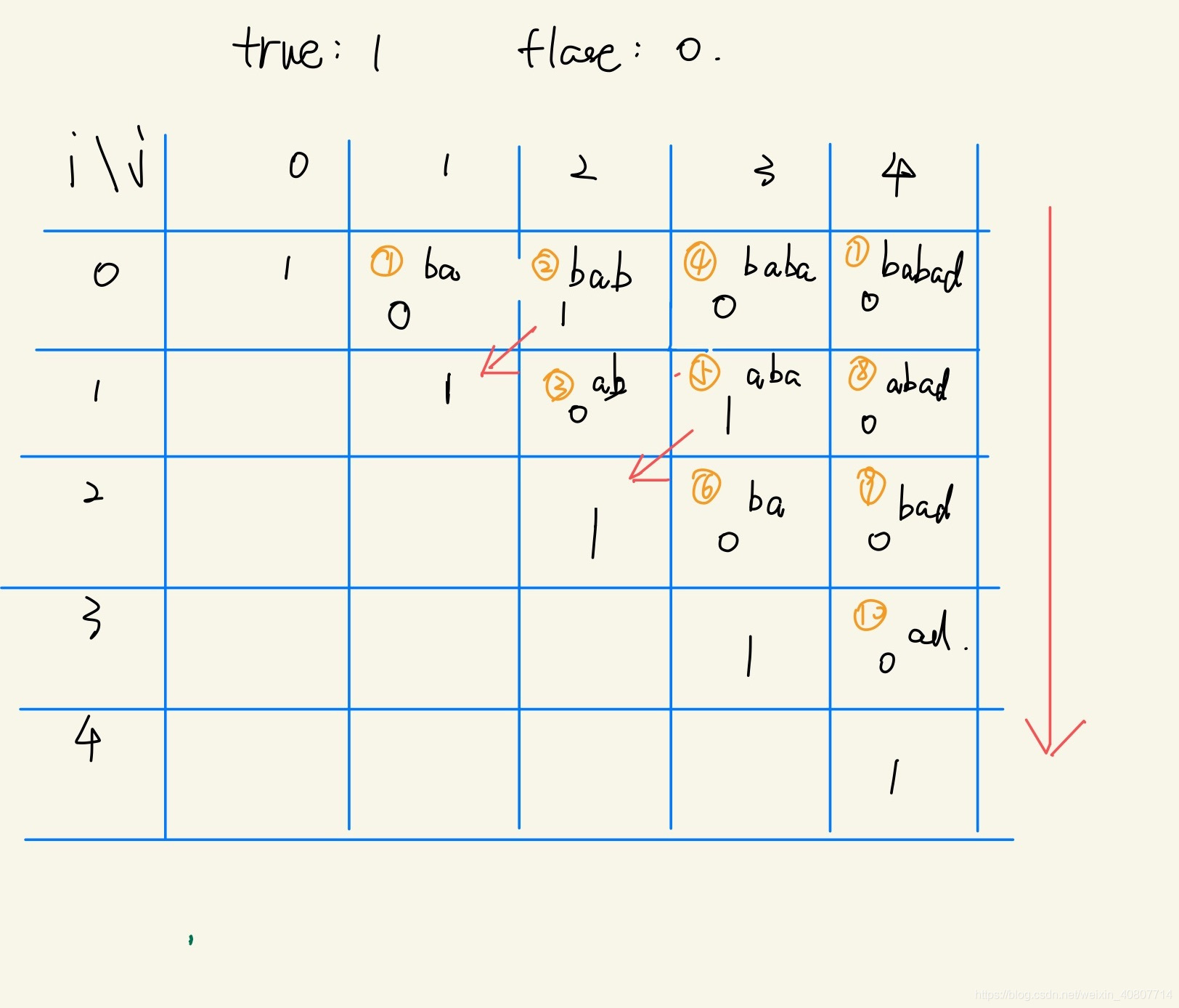
05最长回文子串 - 图1

代码

  1. class Solution {
  2. public:
  3.     string longestPalindrome(string s) {
  4.         if(s.size() <= 1)
  5.             return s;
  7.         int len = s.size();
  8.         bool dp[len][len];
  9.         for(int i = 0; i < len; i++){
  10.             dp[i][i] = true;
  11.         }   
  13.         int maxLen = 1;
  14.         int start = 0;
  16.         for(int j = 0; j < len; j++){
  17.             for(int i = 0; i < j; i++){
  18.                 if(s[i] == s[j]){
  19.                     if(j - i < 3)
  20.                         dp[i][j] = true;
  21.                     else
  22.                         dp[i][j] = dp[i + 1][j - 1];
  23.                 }
  24.                 else
  25.                     dp[i][j] = false;
  27.                 if(dp[i][j]){
  28.                     int temp = j - i + 1;
  29.                     if(temp > maxLen){
  30.                         maxLen = temp;
  31.                         start = i;
  32.                     }
  33.                 }
  34.             }
  35.         } 
  37.         return s.substr(start, maxLen);    
  38.     }
  39. };

参考链接

大神的解答

如果有错误或者不严谨的地方，请务必给予指正，十分感谢。