279完全平方数(优化思路)

题目链接

题目描述：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

实例：

输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.

解题思路

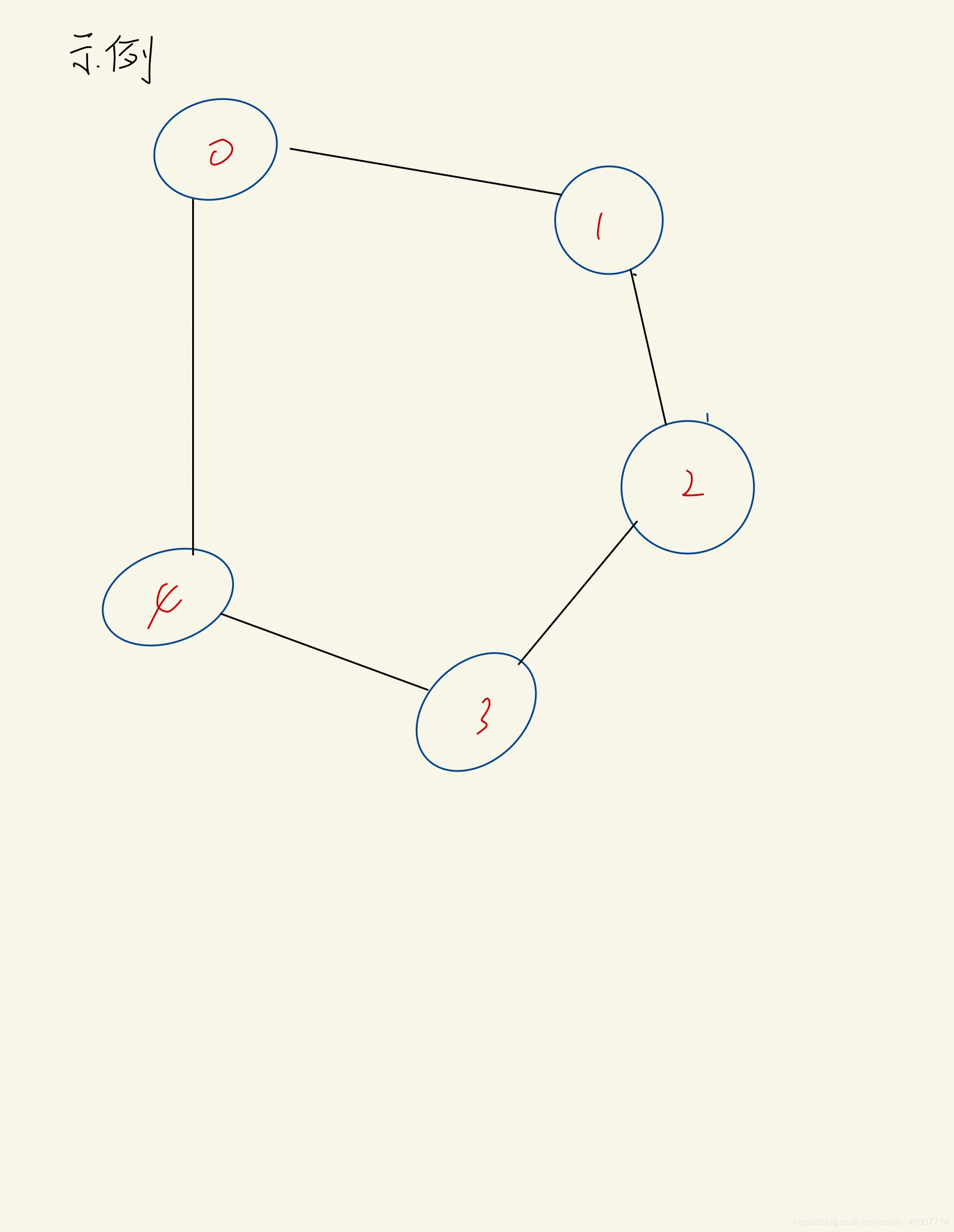
  可以将整个问题转化为图论问题。现在对该问题建模：

• 从n到0每个数字代表每个结点；
• 如果两个数字相差一个完全平方数，则在两结点之间建立一条边；
    这样就得到了一个无权图，原问题转化为求这个无权图从n到0的最短路径。
  
    既然转化为最短路径问题，那就不得不提到队列了，进而该问题转化为队列实现BFS(广度优先搜索)。

代码

class Solution {
public:
    int numSquares(int n) {
        queue< pair<int,int> > q;  //1.当前数字；2.到当前数字的路径的段数
        q.push(make_pair(n,0));
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();
            if(num == 0){
                return step;
            }
            for(int i = 1; num - i*i >= 0; i++){
                q.push(make_pair(num - i*i, step + 1));
            }
        }
        throw invalid_argument("No Solution");
    }
};

  遗憾的是，在leetcode并不能通过，why？

  这看起来像一个BFS，但实际上不是(可以好好看看教材上BFS遍历图的过程，当遇到访问过的结点会怎么做？)。原因在于，循环入队过程中，会有重复结点入队。比如，对于结点1来说，5-4=1、2-1=1、10-9=1等等。我们当前用图建模而不是树建模，对于树结构来说，每一个结点只有一个父结点，意味着到达该结点途径唯一；而对于图结构来说，到达某一结点的路径不唯一。所以，当n足够大时，冗余结点过多，会超出时间限制。

优化1

  既然当前有重复结点存在，那么就让它变得“唯一”。如何做？设置一个长度为n+1的数组，表示从0到n的某一结点是否已经被访问过，访问过置为true，未访问过置为false。循环入队的过程中，当该结点未被访问过，则可以入队。

代码

class Solution {
public:
    int numSquares(int n) {
        queue< pair<int,int> > q;  //1.当前数字；2.到当前数字的路径的段数
        q.push(make_pair(n,0));
        vector<bool> visited(n + 1, false); //表示从0到n，是否已经被访问过
        visited[n] = true;
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();
            if(num == 0){
                return step;
            }
            for(int i = 1; num - i*i >= 0; i++){
                if(!visited[num - i*i]){
                    q.push(make_pair(num - i*i, step + 1));
                    visited[num - i*i] = true;
                }
            }
        }
        throw invalid_argument("No Solution");
    }
};

  虽然leetcode通过了我们的代码，但是执行用时不太友好，显然我们可以再进一步优化。

优化2

  我们通过观察发现了两处优化。
  首先，我们发现在循环入队部分，每一轮num - i*i计算执行了四次，显然这一部分可以做文章。
  其次，另一处优化点，在于是否可以在循环中提前返回最短路径。因为当num - i*i == 0时，显然下一结点为终点(零结点)，我们可以返回step + 1，提前一轮结束遍历。

代码

class Solution {
public:
    int numSquares(int n) {
        queue< pair<int,int> > q;  //1.当前数字；2.到当前数字的路径的段数
        q.push(make_pair(n,0));
        vector<bool> visited(n + 1, false); //表示从0到n，是否已经被访问过
        visited[n] = true;
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();
            for(int i = 1; ; i++){
                int n = num - i*i;
                if(n < 0)
                    break;
                if(n == 0)
                    return step + 1;
                if(!visited[n]){
                    q.push(make_pair(n, step + 1));
                    visited[n] = true;
                }
            }
        }
        throw invalid_argument("No Solution");
    }
};

如果有错误或者不严谨的地方，请务必给予指正，十分感谢。