写在前面

  本人最近准备复试，在刷leetcode过程中遇到了类似于荷兰国旗的问题，于是特意回看了一下快速排序算法，也加深了对其的理解。作为一种feedback的方式，记录一篇笔记总结一下对快排的认识。

目录

  • 概述
  • 基本算法
  • 算法改进
  • 例题

概述

  快速排序是一种基于分治思想的排序算法。它之所以流行的原因有二：一是原地排序，且长度为N的数组排序所需时间与NlgN成正比；二是其内循环比多数排序算法都小。之所以仅有快速排序被称为“快速”，是因为多数排序算法的基本操作次数执行次数的多项式最高次项为X✖️nlog2n(X为系数)，快速排序的X最小。这使得快速排序在同级别算法中最好，因此称为快速排序。另外，快速排序的平均时间复杂度为O(nlog2n)，空间复杂度O(log2n)。

基本算法

  想要理解快速排序，重中之重在于理解切分(paititon)过程。而要理解切分过程，学会使用循环不变量设计扫描指针是绕不开的关卡。文章后面会谈到此概念在快速排序中的应用。
  先将传入的数组划分为两个子数组，将两部分独立排序，之后递归调用处理整个数组。

  1. void quickSort(int nums[], int left, int right){
  2.         if(left >= right)                  //递归结束条件
  3.             return;
  4.         //切分，返回切分元素存放位置
  5.         int i = partition(nums, left, right); 
  6.         //递归调用排序左半部分[left...i-1] 
  7.         quickSort(nums, left, i - 1);  
  8.         //递归调用排序右半部分[i+1...right]    
  9.         quickSort(nums, i + 1, right);      
  10.     }

  接下来到了方法的关键——切分。该过程数组满足下面三个条件：

  • 对于某个i，nums[i]已经排序完毕
  • 左半部分[left…i-1]所有元素均不大于nums[i]
  • 右半部分[i+1…right]所有元素均不小于nums[i]
      过程如下：一般选取nums[left]作为切分元素(或称枢轴),即它是那个chosen one！之后，从数组左端开始扫描直到遇见大于它的元素，再从数组右端开始扫描直到遇见小于它的元素。这两个元素显然并未排序完毕，所以将其两个交换。如此循环，直到左右扫描指针相遇彼此，则此时我们会发现左半部分[left…i-1]所有元素均不大于nums[i]且右半部分[i+1…right]所有元素均不小于nums[i]。即，此时该相遇位置就是切分元素nums[left]的最终位置。
      简易切分示意图如下：
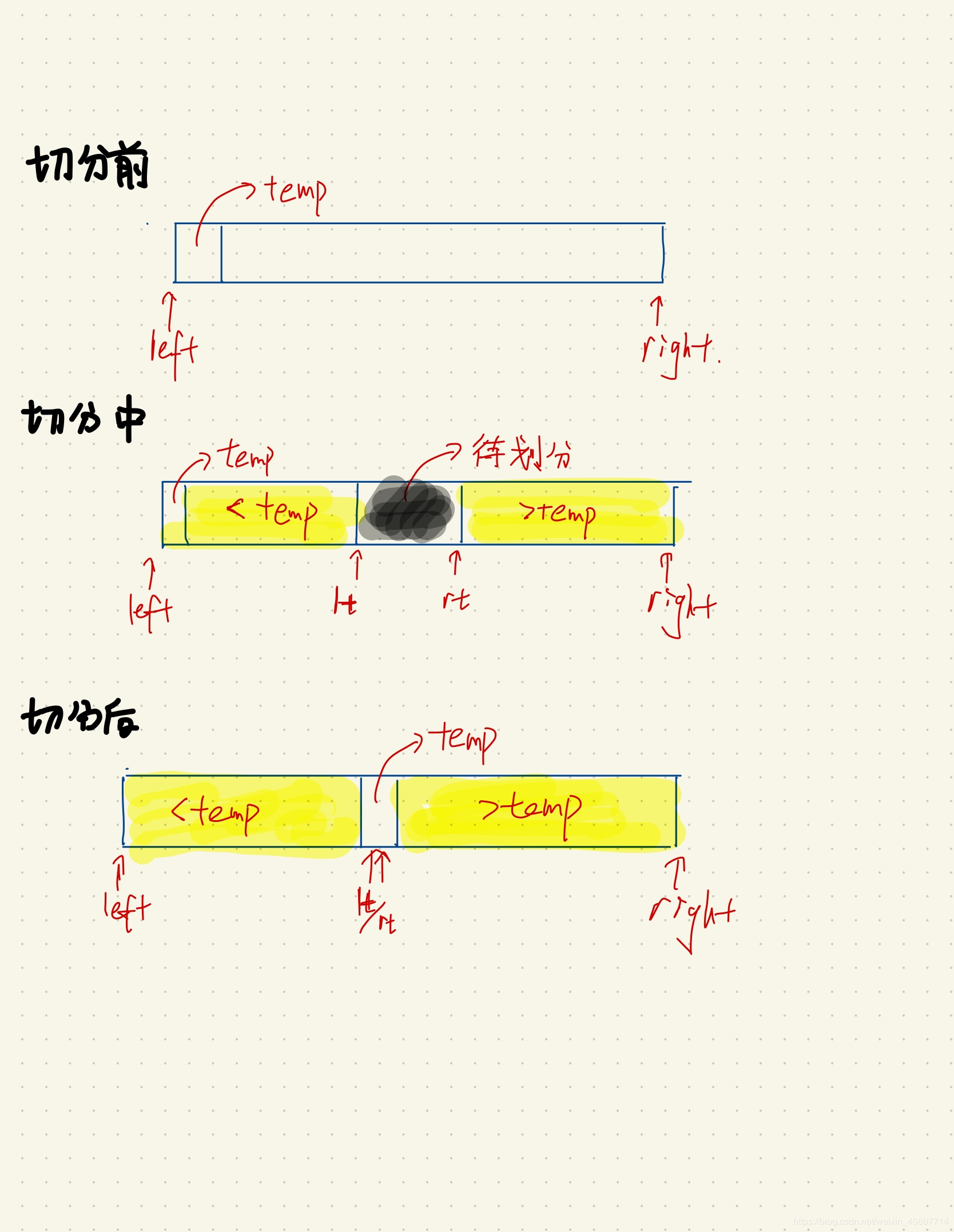
    从设计循环不变量浅谈快速排序 - 图1
      切分(paititon)算法实现过程如下：
  1. int partition(int nums[], int left, int right){
  2.         int temp = nums[left];                  //切分元素(或称枢轴),一般选取输入数组左端值
  3.         int lt = left, rt = right + 1;          //左右扫描指针，此处指针的设计会影响后面"检查大小"与"扫描"这两操作的先后顺序
  4.                                                 //注意：[left...lt) , [rt...right]划分的两数组初始为空
  5.                                                 //     许多常见排序算法的扫描指针的设计都依据循环不变量这一概念
  6.         while(1){
  7.             while(nums[++lt] < temp)   //先扫描后检查大小，向左扫描直到遇见大于temp的值
  8.                 if(lt == right)
  9.                     break;
  10.             while(temp < nums[--rt])    //先扫描后检查大小，向右扫描直到遇见小于temp的值
  11.                 if(rt == left)
  12.                     break;
  13.             if(lt >= rt)                             //当左右扫描指针相遇标志着扫描结束，切分元素位置已找出
  14.                 break;
  15.             swap(nums[lt], nums[rt]);         //交换元素
  16.         }
  18.         swap(nums[left], nums[rt]);                 //将切分元素放置在左右指针相遇位置，返回位置索引
  19.         return rt;
  20.     }

  其中，要注意左右扫描指针的设计，这里涉及到循环不变量的概念，这个概念尤其会应用在后续算法改进中的指针设计。事实上，许多常见的排序算法都要用到循环不变量，平时要多总结，便于深入理解排序算法过程。
  为了加深对循环不变量的理解，在给出另一种扫描指针的设计。

  1. void quickSortSecond(int nums[], int left, int right){ //从左向右，由小到大排序
  2.         int temp;                                //枢轴
  3.         int i = left, j = right;                 //左指针i，右指针j  [left...i) , (j...right]两数组起始为空
  4.         //注意区间开闭情况，这会使后续操作顺序变为先"检查大小"后"扫描"
  5.         if(left < right){                               //递归终止条件
  6.             temp = nums[left];                   //枢轴选取数组的左边界
  7.             while(i < j){
  8.                 while(j > i && nums[j] >= temp)  //j向左扫描，遇到比temp值大的值就继续向左扫描
  9.                     j--;
  10.                 if(i < j)                        //当向左扫描遇到的值小于temp时，将该值赋值到左侧索引i位置
  11.                     nums[i++] = nums[j];         //并且i前进到下一个索引位置，等待扫描开始
  12.                 while(i < j && nums[i] < temp)   //i向右扫描，遇到比temp值小的值就继续向右扫描
  13.                     i++;
  14.                 if(i < j)                        //当向左扫描遇到的值大于temp时，将该值复制到右侧索引j位置
  15.                     nums[j--] = nums[i];         //并且j前进到下一个索引位置，等待扫描开始
  16.             }
  18.             nums[i] = temp;                      //i，j最终相遇位置即为枢轴存放位置
  19.             //下一趟排序开始
  20.             quickSortSecond(nums, left, i - 1);  //左
  21.             quickSortSecond(nums, i + 1, right);  //右
  22.         }
  23.     }

  此时，区间变为[left…i)和(j…right]，切分过程变为先检查大小后扫描。

算法改进

  如果排序代码多次执行或者用于大型数组，那么上面的基本算法可能不再适用。改进方法有多种，具体理论可以去阅读算法(第四版)，经典中的经典！接下来介绍一种改进策略，也是由荷兰国旗问题引出的三路快排算法。
  思路如下：将数组切分成三部分，即分别小于、等于和大于切分元素的子数组(对应荷兰国旗的三种颜色)。设计出三个指针，即lt，rt，mt。并且一般将数组左端元素作为切分元素temp。而后，从左到右扫描数组，使得

[left…lt) < temp (gt…right] > temp [lt…mt) == temp [mt…gt]等待排序

说明：循环不变量设计核心：代码执行过程中始终保持区间全覆盖且其中无重复。(注：可以自己画一个数轴实操一下)
  针对这一核心，解释上面的设计思路：

  • lt为小于temp和等于temp的分界点。为了不重合，一个设计成开区间，另一个就必须是闭区间。即，[left…lt) < temp和[lt…mt) == temp
  • mt为扫描指针，一般设计成开区间。即，[lt…mt) == temp
    准确来说[left…mt)中的元素代表已遍历。
  • gt为等待排序区间和大于temp区间分界点。同样为了不重合，一个设计成开区间，另一个就必须是闭区间。即，[mt…gt]等待排序和(gt…right] > temp。

  另外注意，循环不变量设计思路不唯一，掌握核心即可随意设计。
  接下来，为了将思路落实，我们就要考虑一个问题，如何初始化变量使得以上思路成立？因为这关系到后续算法的两大问题：

  1. 扫描过程中，“加减”和“交换”这两个操作的先后顺序
  2. 递归何时结束

  为落实这三个问题，我们要说明一下切分过程。当指针mt扫描到某处时，遇到的情况无非三种：大于temp，小于temp，等于temp。所以针对这三种情况，我们有三步处理：

  • nums[mt] == temp 加减：mt自增1；
  • nums[mt] > temp 交换：nums[mt]与nums[rt]交换；加减：rt自减1；
  • nums[mt] < temp 交换：nums[mt]与nums[lt]交换；加减：lt自增1，mt自增1；

  其实我们已经注意到“加减”和“交换”两个操作的顺序要根据指针变量的初始化而决定。至于递归何时结束？如果你理解了基本算法思路和循环不变量设计思路，不难发现当指针mt与指针rt相遇时，遍历结束。附上一个三路快排的切分示意图：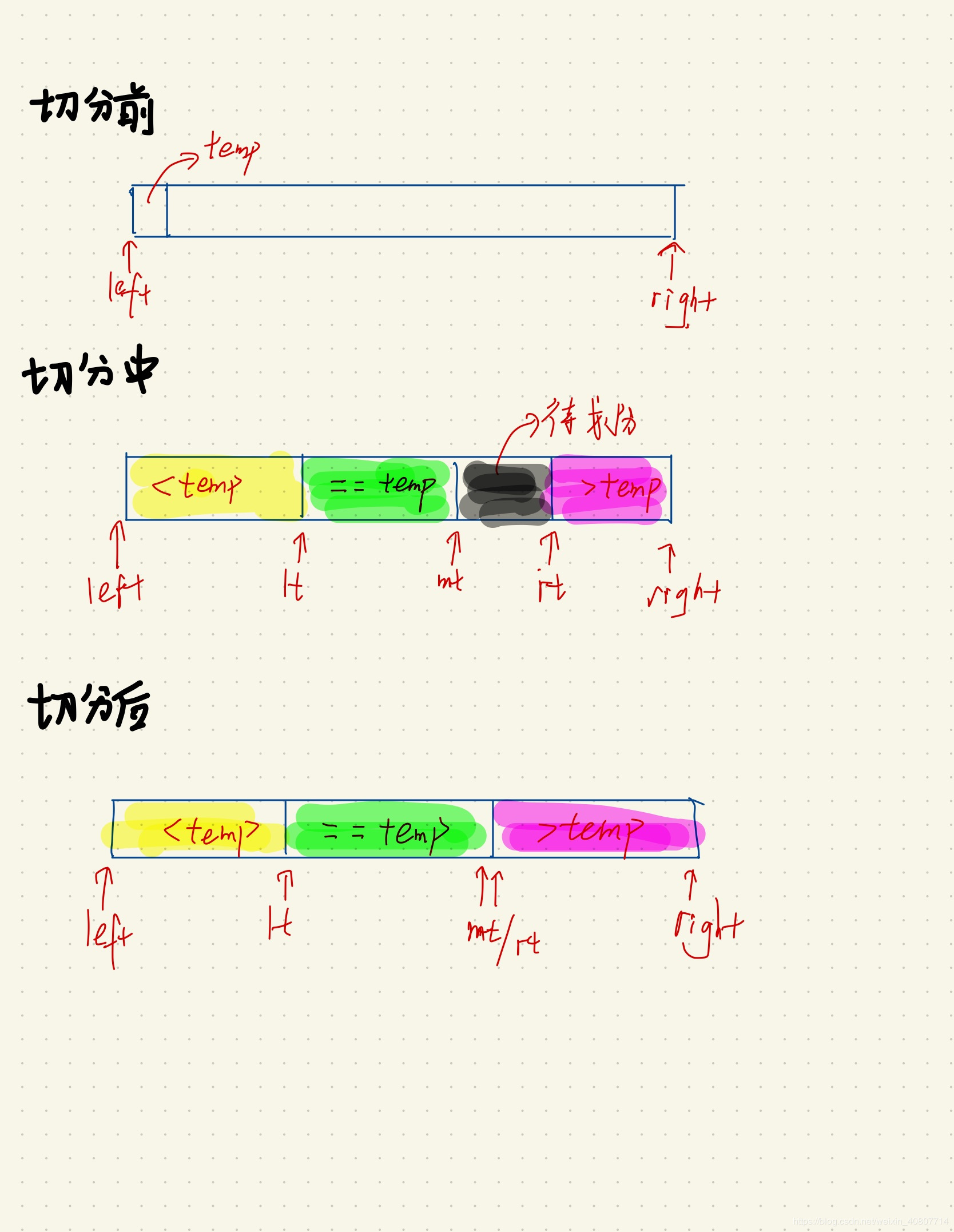
从设计循环不变量浅谈快速排序 - 图2

  现在，让我们回到如何初始化指针变量的问题上来。在基本算法部分我们已经注意到，初始数组一定为空。也就是说，要设计lt，rt指针使得三部分数组在一开始为空。而后，“加减”和“交换”两步操作就看你的初始值如何定义了。以下是算法过程：(注意：此过程不唯一，要根据你设计的循环不变量而定)

  1. void quickThirdSort(int arr[], int left, int right){
  2.         int temp = arr[left];
  3.         int lt = left, rt = right, mt = left + 1;       //[left...lt)<temp, [lt...mt]==temp, (rt...right]>temp
  4.         if(left < right) {                              //判定合法性 
  5.             while(mt <= rt){                            //递归终止条件
  6.                 if(arr[mt] == temp)                 
  7.                     mt++;
  8.                 else if(arr[mt] > temp)
  9.                     swap(arr[mt], arr[rt--]);    //先交换再加减
  10.                 else      //arr[mt] < temp
  11.                     swap(arr[mt++],arr[lt++]);   //先交换再加减
  12.             }
  13.             //现在arr[left...lt) < temp = arr[lt...rt] < arr(rt...right]
  14.             //递归开始
  15.             quickThirdSort(arr, left, lt - 1);
  16.             quickThirdSort(arr, rt + 1, right);
  17.         }
  18.         else{
  19.             return;
  20.         }
  21.     }

例题

  leetcode#75.颜色分类
  题目描述：给定一个包含0、1和2，一共 n 个元素的数组，对它们进行原地排序，使得相同值元素相邻，并按照0、1、2顺序排列。
  实例：

输入: [2,0,2,1,1,0] 输出: [0,0,1,1,2,2]

  思路：

  • 确定数组元素仅包含0、1、2三种值，由此可以采用三路快排方法求解问题；
  • 取1作为切分元素，并设置zero，two两个边界指针，i为扫描指针。此处初始值的设计直接影响到循环边界(i <= two或i == two)以及“加减”和”交换“的操作顺序。其中一种循环自变量定义会在代码中给出。
  • 在循环过程中扫描到某处，简述判断过程：

若等于1，非常简单，自增i就好； 若等于2，显然它属于“2”数组，这时要把它与指针two前(two—)到元素交换，让它归到“2”数组去。同时，我们也要自减two(注意：“加减”和”交换“的操作顺序由初始化变量决定！)这时我们会疑惑交换过来的数不一定为1呀！别着急，一步一步来。 现在对交换过来的元素进行判断。 若为1，前面已经告诉你啦！ 若为0，稍微有点复杂。将zero前(zero++)的元素和该值交换，当然，zero自增1将这个元素收入到“0”数组。此外，我们发现zero前的元素本来就是1(因为zero是“0”数组和“1”数组的分界点)，所以交换过来的元素理应是“1”数组的值，所以i自增。注意：这一步需要自增两个指针，而且顺序还是由循环自变量设计决定！

  • 当i指针与two指针相遇时，循环结束。只需遍历一遍。无需递归

  附上自制过程图：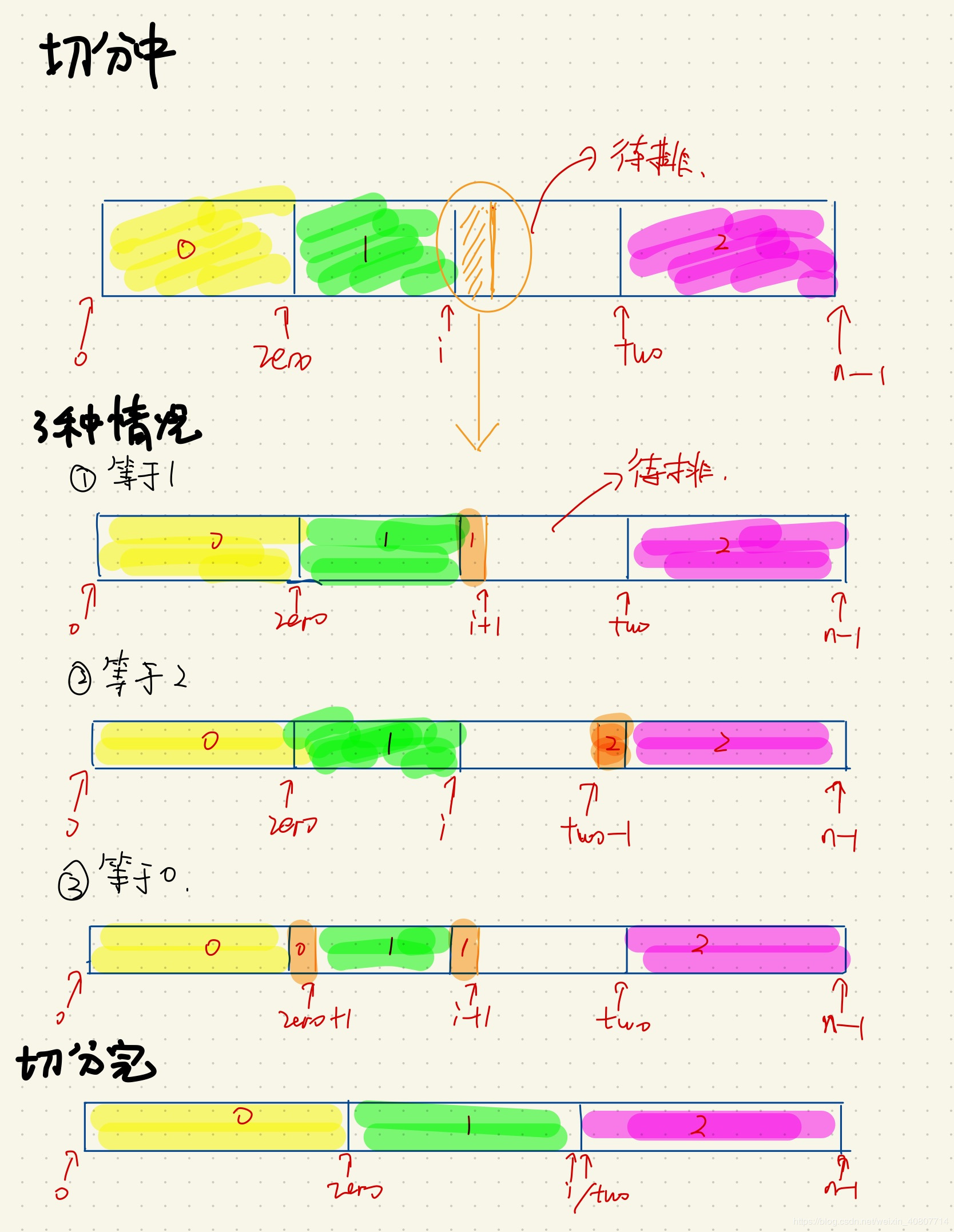
从设计循环不变量浅谈快速排序 - 图3

  算法：

  1. void sortColors(vector<int>& nums) {
  2.         //时间复杂度O(n)
  3.         //空间复杂度(1)
  5.         //循环自变量定义：
  6.         //[0...zero] = 0
  7.         //[zero...i) = 1
  8.         //[i..two)待排序
  9.         //[two...n-1] = 2
  10.         int zero = -1;                            //nums[0...zero] == 0 初始数组为空
  11.         int two = nums.size();                    //nums[two..n-1] == 2 初始数组为空
  12.         for (int i = 0; i < two; ) {
  13.             if(nums[i] == 1){
  14.                 i++;
  15.             }
  16.             else if(nums[i] == 2){
  17.                 swap(nums[i], nums[--two]);
  18.             }
  19.             else{ //nums[i] == 0
  20.                 assert(nums[i] == 0);
  21.                 swap(nums[++zero], nums[i++]);
  22.                 // swap(nums[++zero], nums[i++]);
  23.             }
  24.         }
  25. }

  对本题有什么疑惑，可以去英文版leetcode的discuss区看看大佬们的解答,可能会启发你。
  欢迎同志们指正和讨论，共同进步！

本人blog：http://breadhunter.gitee.io