题目链接

题目描述：

给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。

找到所有在 [1, n] 范围之间没有出现在数组中的数字。

您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:

输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]

思路1

  题目给了两个关键条件，一是数组元素范围为 1 ≤ a[i] ≤ n ( n = 数组大小 )；二是数组元素出现次数要么是两次，要么是一次，这为解题创造了前提。这很容易让我们联想到“一个萝卜一个坑”，现在“萝卜”是乱的，我们该如何让萝卜回到它自己的坑呢？如果“萝卜”回到了它自己对应的坑，那么重复的萝卜就会散落在别的坑里，这些“别的坑”里原本应该对应的“萝卜”就是输出结果。换而言之就是按索引排序～
  说的太抽象，画一个示意图有助理解～
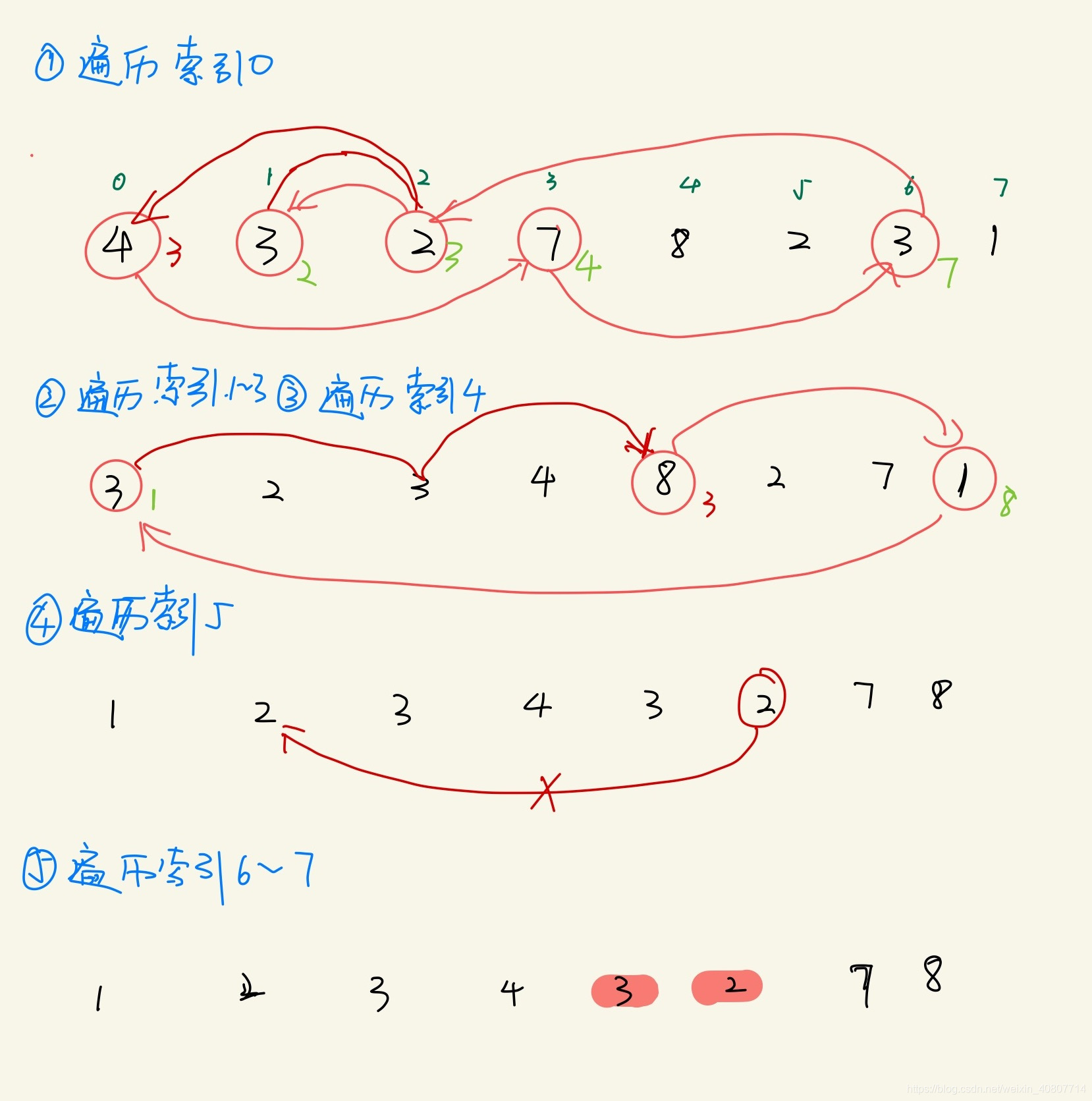
448找到所有数组中消失的数字 - 图1

  另外，针对一个测试用例[2，1]添加了一个判断。

if(nums[i] != i + 1)
   nums[i] = temp;

代码

  1. class Solution {
  2. public:
  3.     vector<int> findDisappearedNumbers(vector<int>& nums) {
  4.         for(int i = 0; i < nums.size(); i++){
  5.             if(nums[i] != i + 1){
  6.                 int temp = nums[i];
  7.                 while(nums[temp - 1] != temp){
  8.                     int record = nums[temp - 1];
  9.                     nums[temp - 1] = temp;
  10.                     temp = record;
  11.                 }
  12.                 //添加判断
  13.                 if(nums[i] != i + 1)
  14.                     nums[i] = temp;
  15.             }
  16.         }
  18.         vector<int> result;
  19.         for(int i = 0; i < nums.size(); i++)
  20.             if(nums[i] != i + 1)
  21.                 result.push_back(i + 1);
  23.         return result;
  24.     }
  25. };

思路2

  进阶要求时间复杂度为O(n)，显然思路1达不到该要求，所以我们要进一步思考。其实如果不要求空间复杂度O(1)的话，我们可以用哈希表存储，find一下即可求出未出现的数字。
  那么我们是否可以在原数组中构建一种简易的哈希表？遍历数组，将数组元素所对应的索引下的值取相反数，那么显然未出现的元素是不能将原本它对应的索引下的值变成负数的，也就是说再次遍历数组，谁为正数，那么正数所在的索引 + 1就是未出现的数字。

原数组：[4, 3, 2, 7, 8, 2, 3, 1]
现数组：[-4, -3, -2, -7, 8, 2, -3, -1]

代码

  1. class Solution {
  2. public:
  3.     vector<int> findDisappearedNumbers(vector<int>& nums) {
  4.         for(int i = 0; i < nums.size(); i++){
  5.             int loc = abs(nums[i]) - 1;
  6.             if(nums[loc] > 0)
  7.                 nums[loc] *= -1;
  8.         }
  10.         vector<int> result;
  11.         for(int i = 0; i < nums.size(); i++)
  12.             if(nums[i] > 0)
  13.                 result.push_back(i + 1);
  15.         return result;
  16.     }
  17. };

如果有错误或者不严谨的地方，请务必给予指正，十分感谢。