题目链接

题目描述：

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

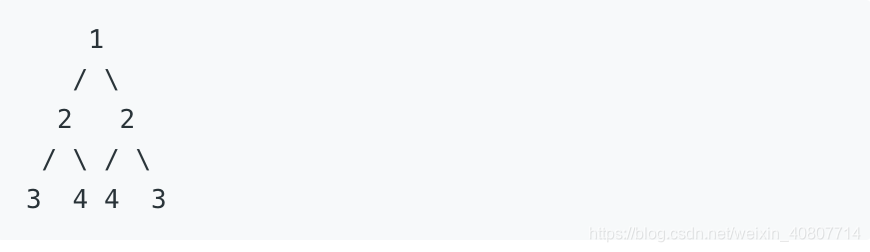
101对称二叉树 - 图1

解题思路&代码

递归

  本题与#100类似，题解在此～

  1. 题意是要求判断对称树，本质上来说还是判断两个树的关系。然主函数只给了一个参数root，所以可以考虑添加辅助函数增加参数列表
  2. 确定两个递归终止条件：一、显然两结点同时为空，那么肯定是相同了；二、如果在两结点中，一个为空，另一个不为空，显然不相同。注意：代码顺序不要改变，因为情况1用到的逻辑运算符为&&，情况2用到的逻辑运算符为||，显然2在1之前会涵盖1的情况。其实，本质上来说，情况2属于异或
  3. 剩下的代码本质上来说就是先序遍历的递归框架

代码

  1. class Solution {
  2. public:
  3.     bool isSymmetric(TreeNode* root) {
  4.         return helper(root, root);
  5.     }
  7.     bool helper(TreeNode* node1, TreeNode* node2){
  8.         if(!node1 && !node2)
  9.             return true;
  10.         if(!node1 || !node2)
  11.             return false;
  12.         if(node1->val != node2->val)
  13.             return false;
  14.         return helper(node1->left, node2->right) && helper(node1->right, node2->left);
  15.     }
  16. };

迭代

  本文以队列举例(栈也可以)。
  根据上面递归的过程，本质上来说我们还是用两个树作对比判断是否对称。于是我们可以利用队列的特点(先进先出)，一次出队两个结点，然后作比较。此过程类似于BFS。
  我们需要关注的是在两个结点的过程中发生了什么，其他的交给循环迭代。那么在这个过程中发生了什么？

  1. 从队列中取出两个结点并将两结点出队
  2. 对照递归的两个终止条件(同为空或者异或)
  3. 判断两个值是否相等。如果是对称的，队列中每两个结点应该是连续相等的。
  4. 之后就是进队操作。按两个结点的左右子结点相反的顺序入队。

代码

  1. class Solution {
  2. public:
  3.     bool isSymmetric(TreeNode* root) {
  4.         if(!root)
  5.             return true;
  6.         queue<TreeNode*> record;
  7.         record.push(root->left);
  8.         record.push(root->right);
  9.         while(!record.empty()){
  10.             TreeNode* node1 = record.front();
  11.             record.pop();
  12.             TreeNode* node2 = record.front();
  13.             record.pop();
  15.             if(!node1 && !node2)
  16.                 continue;
  17.             if(!node1 || !node2)
  18.                 return false;
  19.             if(node1->val != node2->val)
  20.                 return false;
  21.             record.push(node1->left);
  22.             record.push(node2->right);
  23.             record.push(node1->right);
  24.             record.push(node2->left);
  25.         }
  26.         return true;
  27.     }
  28. };

如果有错误或者不严谨的地方，请务必给予指正，十分感谢。