一、任务需求
用电量问题:
房主对家用电器在他家的电量消耗很关注,因此他计录了21 天中每天空调器使用的小时数,他还监测了这些天的电表并计算出使用的千瓦时(度)数,同时还记录了烘干器每天使用的次数(数据见表1.1)。房主想搞清楚用电量与空调器使用的小时数和烘干器每天使用的次数之间的关系,希望建立一个简单的经验公式来实现。
家用电器用电量数据表如下: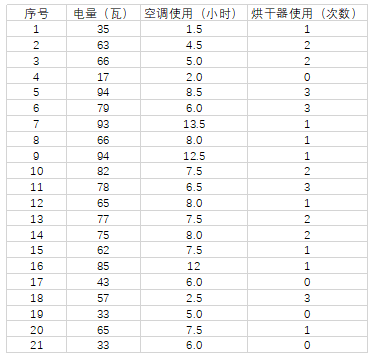
二、分析目标
为了直观地表示用电量与空调器使用的小时数和烘干器每天使用的次数之间的关系,可以将用电量视为因变量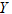 ,空调器使用的小时数和烘干器每天使用的次数视为自变量
,空调器使用的小时数和烘干器每天使用的次数视为自变量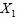 和
和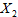 ,
,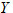 和
和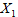 ,
,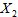 是可观测的变量,由这些变量的取值不能完全决定每天的用电总量。
是可观测的变量,由这些变量的取值不能完全决定每天的用电总量。
在这些情况下,我们认为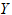 由两部分构成,一部分是由
由两部分构成,一部分是由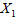 ,
,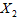 能够决定的部分,它是
能够决定的部分,它是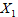 ,
,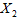 的某个函数,记为
的某个函数,记为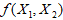 ,另一部分是从众多未加考虑因素所产生的影响,被看作是随机误差,记为
,另一部分是从众多未加考虑因素所产生的影响,被看作是随机误差,记为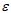 ,它的值是不可观测的,由此可建立多元线性回归模型。
,它的值是不可观测的,由此可建立多元线性回归模型。
三、数学模型
3.1 提出假设
1) 假设无记录错的或因测量仪器故障而收集到的异常数据
2) 假设各分量相互独立,均服从均值为0,方差为的正态分布,即
3.2 符号约定
3.3 线性回归模型
设用电总量为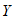 (因变量),空调器每天使用小时数为
(因变量),空调器每天使用小时数为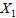 ,烘干器每天使用次数为
,烘干器每天使用次数为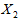 ,家用电器用电量数据表中对
,家用电器用电量数据表中对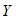 与
与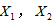 进行21次独立观测,得到21组观测值(样本数据):
进行21次独立观测,得到21组观测值(样本数据):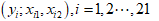
它们满足关系式: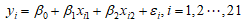
于是因变量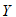 跟自变量
跟自变量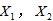 的关系可以表示为:
的关系可以表示为: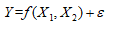
为建立多元线性回归模型,需要进行回归分析,即利用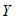 与
与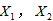 的观测数据,误差项的某些假定下
的观测数据,误差项的某些假定下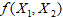 ,利用统计推断方法对所确定的函数的合理性以及由此关系所揭示的
,利用统计推断方法对所确定的函数的合理性以及由此关系所揭示的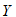 与
与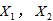 的关系为线性,于是可以建立
的关系为线性,于是可以建立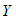 与
与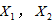 的多元线性回归模型如下:
的多元线性回归模型如下: 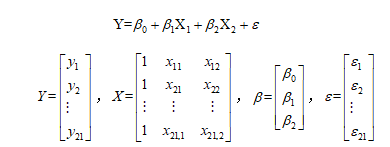
其中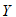 与
与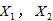 是已知的,由样本数据所决定,
是已知的,由样本数据所决定,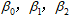 是待估的参数回归向量,
是待估的参数回归向量,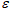 称为回归参数,是不可观测的随机误差向量。
称为回归参数,是不可观测的随机误差向量。
3.4 逐步回归法
逐步回归法就是依次拟合一系列回归方程,后一个方程是在前一个的基础上添加或删除一个自变量,其添加或删除某个自变量的准则是用残差平方和的相对减少量或增加量来衡量。由上述问题可建立两个回归模型如下:
通过比较分析,从而选择出“最优”的回归方程。
四、数据分析
逐步回归分析既可以在一定程度上避免多重共线性的变量同时进入方程,也可以剔除不显著的自变量。
[数据集1]
| 输入/移去的变量a | |||
|---|---|---|---|
| 模型 | 输入的变量 | 移去的变量 | 方法 |
| 1 | 空调使用(小时) | . | 步进(准则: F-to-enter 的概率 <= .050,F-to-remove 的概率 >= .100)。 |
| 2 | 烘干器使用(次数) | . | 步进(准则: F-to-enter 的概率 <= .050,F-to-remove 的概率 >= .100)。 |
| a. 因变量: 电量(瓦) |
定义显著性水平为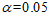 ,首先剔除自变量空调使用时间,然后剔除自变量烘干器使用次数。
,首先剔除自变量空调使用时间,然后剔除自变量烘干器使用次数。
| 模型汇总c | |||||
|---|---|---|---|---|---|
| 模型 | R | R 方 | 调整 R 方 | 标准 估计的误差 | Durbin-Watson |
| 1 | .765a | .586 | .564 | 14.453 | |
| 2 | .985b | .971 | .968 | 3.935 | 1.700 |
| a. 预测变量: (常量), 空调使用(小时)。 b. 预测变量: (常量), 空调使用(小时), 烘干器使用(次数)。 c. 因变量: 电量(瓦) |
|||||
Durbin-Watson用来检验残差自相关,值越接近2时,不存在自相关,即残差相互独立;越小于2偏向0或大于2偏向4,存在自相关。
由于图表中Durbin-Watson的值为1.700,故不存在自相关,即残差相互独立
回归方程的检验系数是0.971,自变量检验了97.1%的因变量
| Anovac | ||||||
|---|---|---|---|---|---|---|
| 模型 | 平方和 | df | 均方 | F | Sig. | |
| 1 | 回归 | 5609.663 | 1 | 5609.663 | 26.855 | .000a |
| 残差 | 3968.909 | 19 | 208.890 | |||
| 总计 | 9578.571 | 20 | ||||
| 2 | 回归 | 9299.802 | 2 | 4649.901 | 300.241 | .000b |
| 残差 | 278.770 | 18 | 15.487 | |||
| 总计 | 9578.571 | 20 | ||||
| a. 预测变量: (常量), 空调使用(小时)。 b. 预测变量: (常量), 空调使用(小时), 烘干器使用(次数)。 c. 因变量: 电量(瓦) |
得到两个逐步回归方程,定义显著性水平为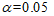 ,它们的回归系数Sig均为0,小于
,它们的回归系数Sig均为0,小于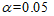 ,故因变量与自变量的线性关系显著。
,故因变量与自变量的线性关系显著。
回归平方和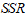 :反映了自变量的线性函数在各组中观测值处取值的离差平方和,越大,表示因变量与自变量的线性关系越显著。
:反映了自变量的线性函数在各组中观测值处取值的离差平方和,越大,表示因变量与自变量的线性关系越显著。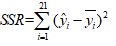
残差平方和: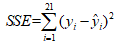
总离差平方和: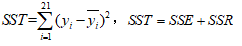
复相关系数的平方: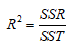
模型2比模型1的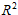 大,故模型2的因变量与自变量的线性关系较显著,故选择模型2作为拟合的线性回归模型。
大,故模型2的因变量与自变量的线性关系较显著,故选择模型2作为拟合的线性回归模型。
| 系数a | |||
|---|---|---|---|
| 模型 | 非标准化系数 | ||
| B | 标准 误差 | ||
| 1 | (常量) | 27.851 | 7.807 |
| 空调使用(小时) | 5.341 | 1.031 | |
| 2 | (常量) | 8.105 | 2.481 |
| 空调使用(小时) | 5.466 | .281 | |
| 烘干器使用(次数) | 13.217 | .856 |
| 系数a | ||||||
|---|---|---|---|---|---|---|
| 模型 | 标准系数 | t | Sig. | 共线性统计量 | ||
| 试用版 | 容差 | VIF | ||||
| 1 | (常量) | 3.568 | .002 | |||
| 空调使用(小时) | .765 | 5.182 | .000 | 1.000 | 1.000 | |
| 2 | (常量) | 3.267 | .004 | |||
| 空调使用(小时) | .783 | 19.469 | .000 | .999 | 1.001 | |
| 烘干器使用(次数) | .621 | 15.436 | .000 | .999 | 1.001 |
a. 因变量: 电量(瓦)
2)标准化的偏回归系数反映了不同自变量对因变量的影响程度,空调使用(小时)的值为0.783,烘干器使用(次数)的值为0.621,对电量使用量影响最大的是空调使用的时间,其次是烘干器使用的次数。
3)Sig表示对偏回归系数的显著性检验,定义显著性水平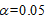 ,空调使用时间和烘干器使用次数的Sig的值都接近于0,故两者的的偏回归系数均达到了显著性水平。
,空调使用时间和烘干器使用次数的Sig的值都接近于0,故两者的的偏回归系数均达到了显著性水平。
4)容差(容忍度)大于0.2, 故不存在多重共线性。
5)VIF(方差膨胀系数)即容差的倒数小于5,故不存在多重共线性。
| 已排除的变量b | |||||
|---|---|---|---|---|---|
| 模型 | Beta In | t | Sig. | 偏相关 | |
| 1 | 烘干器使用(次数) | .621a | 15.436 | .000 | .964 |
| 已排除的变量b | ||||
|---|---|---|---|---|
| 模型 | 共线性统计量 | |||
| 容差 | VIF | 最小容差 | ||
| 1 | 烘干器使用(次数) | .999 | 1.001 | .999 |
| a. 模型中的预测变量: (常量), 空调使用(小时)。 b. 因变量: 电量(瓦) |
| 共线性诊断a | ||||||
|---|---|---|---|---|---|---|
| 模型 | 维数 | 特征值 | 条件索引 | 方差比例 | ||
| (常量) | 空调使用(小时) | 烘干器使用(次数) | ||||
| 1 | 1 | 1.915 | 1.000 | .04 | .04 | |
| 2 | .085 | 4.739 | .96 | .96 | ||
| 2 | 1 | 2.652 | 1.000 | .02 | .02 | .04 |
| 2 | .274 | 3.112 | .02 | .18 | .79 | |
| 3 | .074 | 5.978 | .96 | .80 | .18 | |
| a. 因变量: 电量(瓦) |
共线性诊断采用主成分特征值法
1)当只有一个自变量时,不存在多重共线性问题;
2)当有两个自变量时,对三个变量(常量和自变量)进行主成分提取,三个主成分的特征值分别为2.652,0.274,0.074,只有一个主成分特征值接近于0,条件指数均小于30,两者方差比例差异明显,从自变量的角度不存在多重共线性;
由此可知,选择模型2所对应的经验回归方程更合理。
| 残差统计量a | |||||
|---|---|---|---|---|---|
| 极小值 | 极大值 | 均值 | 标准 偏差 | N | |
| 预测值 | 19.04 | 95.11 | 64.86 | 21.564 | 21 |
| 残差 | -7.901 | 6.467 | .000 | 3.733 | 21 |
| 标准 预测值 | -2.125 | 1.403 | .000 | 1.000 | 21 |
| 标准 残差 | -2.008 | 1.643 | .000 | .949 | 21 |
| a. 因变量: 电量(瓦) |
图表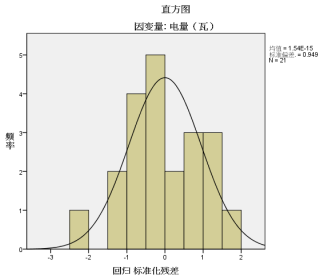
由残差的正直方图可知,残差基本满足正态分布。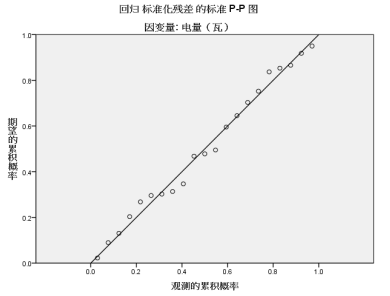
由于图中散点是接近直线的,散点大致在一条直线上,故有理由认为残差服从正态分布。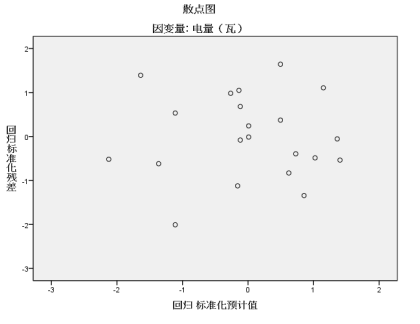
现有的数据与线性关系假设与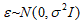 的假设没有明显不一致的征兆,即相应的假设是合理的。残差基本上在0为横轴的直线上下随机波动,且没有离群值(异常值),故残差方差是稳定的。
的假设没有明显不一致的征兆,即相应的假设是合理的。残差基本上在0为横轴的直线上下随机波动,且没有离群值(异常值),故残差方差是稳定的。
五、总结
利用软件SPSS进行数据分析,进行了回归方程的显著性检验,回归系数的统计推断,误差想的正态性检验(学生化残差、残差正态性的频率检验和残差的正太QQ图检验)和残差图分析。通过比较,选择模型2作为拟合的线性回归模型,得到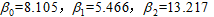 ,故拟合的回归方程为:
,故拟合的回归方程为: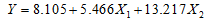
例如,下面比较模型1与模型2的共线性诊断(采用主成分特征值法)中主成分的特征值,复相关系数的平方的值,从而确定了“最优”的回归模型。
1.共线性诊断
1)当只有一个自变量时,不存在多重共线性问题;
2)当有两个自变量时,对三个变量(常量和自变量)进行主成分提取,三个主成分的特征值分别为2.652,0.274,0.074,只有一个主成分特征值接近于0,条件指数均小于30,两者方差比例差异明显,从自变量的角度不存在多重共线性;
由此可知,选择模型2所对应的经验回归方程更合理。
2.复相关系数的平方
设模型1与模型2复相关系数的平方分别为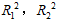 :
: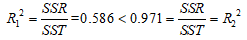
模型2的因变量与自变量的线性关系较显著,故选择模型2作为拟合的线性回归模型。


