一、任务需求
1991 年我国30个省、区、市城镇居民月平均消费八个指标（单位均为元/人）
X1: 人均粮食支出 X2: 人均副食支出
X3: 人均烟茶支出 X4: 人均其它副食支出
X5: 人均衣着商品支出 X6: 人均日用品支出
X7: 人均燃料支出 X8: 人均非商品支出
1991 年我国30个省、区、市城镇居民月均消费数据如下：
| 省区市 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
|---|---|---|---|---|---|---|---|---|
| 山西 | 8.35 | 23.53 | 7.51 | 8.62 | 17.42 | 10.00 | 1.04 | 11.21 |
| 内蒙古 | 9.25 | 23.75 | 6.61 | 9.19 | 17.77 | 10.48 | 1.72 | 10.51 |
| 吉林 | 8.19 | 30.50 | 4.72 | 9.78 | 16.28 | 7.60 | 2.52 | 10.32 |
| 黑龙江 | 7.73 | 29.20 | 5.42 | 9.43 | 19.29 | 8.49 | 2.52 | 10.00 |
| 河南 | 9.42 | 27.93 | 8.20 | 8.14 | 16.17 | 9.42 | 1.55 | 9.76 |
| 甘肃 | 9.16 | 27.98 | 9.01 | 9.32 | 15.99 | 9.10 | 1.82 | 11.35 |
| 青海 | 10.06 | 28.64 | 10.52 | 10.05 | 16.18 | 8.39 | 1.96 | 10.81 |
| 河北 | 9.09 | 28.12 | 7.40 | 9.62 | 17.26 | 11.12 | 2.49 | 12.56 |
| 陕西 | 9.41 | 28.20 | 5.77 | 10.80 | 16.36 | 11.56 | 1.53 | 12.17 |
| 宁夏 | 8.70 | 28.12 | 7.21 | 10.53 | 19.45 | 13.30 | 1.66 | 11.96 |
| 新疆 | 6.93 | 29.85 | 4.54 | 9.49 | 16.62 | 10.65 | 1.88 | 13.61 |
| 湖北 | 8.67 | 36.05 | 7.31 | 7.75 | 16.67 | 11.68 | 2.83 | 12.88 |
| 云南 | 9.98 | 37.69 | 7.01 | 8.94 | 16.15 | 11.08 | 0.83 | 11.67 |
| 湖南 | 6.77 | 38.69 | 6.01 | 8.82 | 14.79 | 11.44 | 1.74 | 13.23 |
| 安徽 | 8.14 | 37.75 | 9.61 | 8.49 | 13.15 | 9.76 | 1.28 | 11.28 |
| 贵州 | 7.67 | 35.71 | 8.04 | 8.31 | 15.13 | 7.76 | 1.41 | 13.25 |
| 辽宁 | 7.90 | 39.77 | 8.49 | 12.94 | 19.27 | 11.05 | 2.04 | 13.29 |
| 四川 | 7.18 | 40.91 | 7.32 | 8.94 | 17.60 | 12.75 | 1.14 | 14.08 |
| 山东 | 8.82 | 33.70 | 7.59 | 10.98 | 18.82 | 14.73 | 1.78 | 10.10 |
| 江西 | 6.25 | 35.02 | 4.72 | 6.28 | 10.03 | 7.15 | 1.93 | 10.39 |
| 福建 | 10.60 | 52.41 | 7.70 | 9.98 | 12.53 | 11.70 | 2.31 | 14.69 |
| 广西 | 7.27 | 52.65 | 3.84 | 9.16 | 13.03 | 15.26 | 1.98 | 14.57 |
| 海南 | 13.445 | 55.85 | 5.50 | 7.45 | 9.55 | 9.52 | 2.21 | 16.30 |
| 天津 | 10.85 | 44.68 | 7.32 | 14.51 | 17.13 | 12.08 | 1.26 | 11.57 |
| 江苏 | 7.21 | 45.79 | 7.66 | 10.36 | 16.56 | 12.86 | 2.25 | 11.69 |
| 浙江 | 7.68 | 50.37 | 11.35 | 13.30 | 19.25 | 14.59 | 2.75 | 14.87 |
| 北京 | 7.78 | 48.44 | 8.00 | 20.51 | 22.12 | 15.73 | 1.15 | 16.61 |
| 西藏 | 7.94 | 39.65 | 20.97 | 20.82 | 22.52 | 12.41 | 1.75 | 7.90 |
| 上海 | 8.28 | 64.34 | 8.00 | 22.22 | 20.06 | 15.12 | 0.72 | 22.89 |
| 广东 | 12.47 | 76.39 | 5.52 | 11.24 | 14.52 | 22.00 | 5.46 | 25.50 |
对此问题进行主成分分析，提取数据包含的实际意义，并作出结论。
二、数学模型
对问题进行初步分析，计算各变量的的方差分别为 2.606,154.723,9.319，
15.171,8.987,9.352,0.747，13.235 通过比较各变量的方差差异不是很大，应考虑从样本协方差矩阵S出发进行主成分析。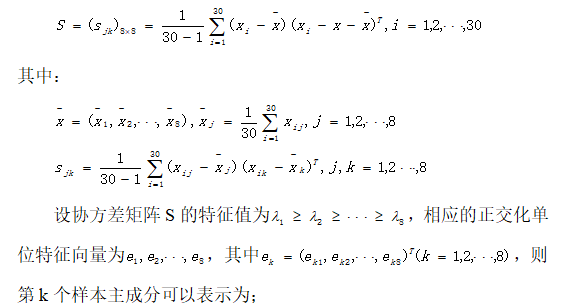
三、数据分析
描述
| 描述统计量 | |||
|---|---|---|---|
| N | 标准差 | 方差 | |
| X1 | 30 | 1.6142219 | 2.606 |
| X2 | 30 | 12.4387583 | 154.723 |
| X3 | 30 | 3.0527165 | 9.319 |
| X4 | 30 | 3.8949558 | 15.171 |
| X5 | 30 | 2.9978548 | 8.987 |
| X6 | 30 | 3.05811 | 9.352 |
| X7 | 30 | .8641566 | .747 |
| X8 | 30 | 3.63796 | 13.235 |
| 有效的 N （列表状态） | 30 |
因子分析
| 附注 | ||
|---|---|---|
| 创建的输出 | 30-4月-2021 09时29分50秒 | |
| 注释 | ||
| 输入 | 活动的数据集 | 数据集1 |
| 过滤器 | ||
| 权重 | ||
| 拆分文件 | ||
| 工作数据文件中的 N 行 | 30 | |
| 缺失值处理 | 对缺失的定义 | MISSING=EXCLUDE：用户定义的缺失值作为缺失对待。 |
| 使用的案例 | LISTWISE：统计量基于对所使用任何变量都不含缺失值的案例。 | |
| 语法 | FACTOR /VARIABLES X1 X2 X3 X4 X5 X6 X7 X8 /MISSING LISTWISE /ANALYSIS X1 X2 X3 X4 X5 X6 X7 X8 /PRINT UNIVARIATE INITIAL CORRELATION SIG KMO AIC EXTRACTION FSCORE /PLOT ROTATION /CRITERIA FACTORS(8) ITERATE(25) /EXTRACTION PC /ROTATION NOROTATE /METHOD=COVARIANCE. |
|
| 资源 | 处理器时间 | 00 00:00:00.328 |
| 已用时间 | 00 00:00:00.450 | |
| 所需的最大内存 | 9080 (8.867K) 字节 |
| 描述统计量 | |||
|---|---|---|---|
| 均值 | 标准差 | 分析 N | |
| X1 | 8.706500 | 1.6142219 | 30 |
| X2 | 39.056000 | 12.4387583 | 30 |
| X3 | 7.629000 | 3.0527165 | 30 |
| X4 | 10.865667 | 3.8949558 | 30 |
| X5 | 16.589000 | 2.9978548 | 30 |
| X6 | 11.6260 | 3.05811 | 30 |
| X7 | 1.917000 | .8641566 | 30 |
| X8 | 13.0340 | 3.63796 | 30 |
| 相关矩阵 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | ||
| 相关 | X1 | 1.000 | .334 | -.054 | -.061 | -.289 | .199 | .343 | .326 |
| X2 | .334 | 1.000 | -.023 | .399 | -.156 | .711 | .403 | .837 | |
| X3 | -.054 | -.023 | 1.000 | .533 | .497 | .033 | -.139 | -.258 | |
| X4 | -.061 | .399 | .533 | 1.000 | .698 | .468 | -.183 | .317 | |
| X5 | -.289 | -.156 | .497 | .698 | 1.000 | .280 | -.205 | -.084 | |
| X6 | .199 | .711 | .033 | .468 | .280 | 1.000 | .411 | .701 | |
| X7 | .343 | .403 | -.139 | -.183 | -.205 | .411 | 1.000 | .399 | |
| X8 | .326 | .837 | -.258 | .317 | -.084 | .701 | .399 | 1.000 | |
| Sig.（单侧） | X1 | .036 | .387 | .374 | .061 | .146 | .032 | .039 | |
| X2 | .036 | .452 | .014 | .205 | .000 | .014 | .000 | ||
| X3 | .387 | .452 | .001 | .003 | .432 | .232 | .084 | ||
| X4 | .374 | .014 | .001 | .000 | .005 | .166 | .044 | ||
| X5 | .061 | .205 | .003 | .000 | .067 | .139 | .330 | ||
| X6 | .146 | .000 | .432 | .005 | .067 | .012 | .000 | ||
| X7 | .032 | .014 | .232 | .166 | .139 | .012 | .015 | ||
| X8 | .039 | .000 | .084 | .044 | .330 | .000 | .015 |
| KMO 和 Bartlett 的检验a | ||
|---|---|---|
| 取样足够度的 Kaiser-Meyer-Olkin 度量。 | .567 | |
| Bartlett 的球形度检验 | 近似卡方 | 143.860 |
| df | 28 | |
| Sig. | .000 | |
| a. 基于相关 |
| 反映像矩阵 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | ||
| 反映像协方差 | X1 | .752 | .028 | -.095 | -.023 | .080 | -.030 | -.118 | -.064 |
| X2 | .028 | .110 | -.051 | -.073 | .097 | -.085 | -.056 | -.076 | |
| X3 | -.095 | -.051 | .431 | -.079 | -.036 | .036 | -.084 | .155 | |
| X4 | -.023 | -.073 | -.079 | .145 | -.113 | .044 | .133 | -.016 | |
| X5 | .080 | .097 | -.036 | -.113 | .157 | -.110 | -.065 | -.020 | |
| X6 | -.030 | -.085 | .036 | .044 | -.110 | .255 | -.059 | -.025 | |
| X7 | -.118 | -.056 | -.084 | .133 | -.065 | -.059 | .535 | -.027 | |
| X8 | -.064 | -.076 | .155 | -.016 | -.020 | -.025 | -.027 | .192 | |
| 反映像相关 | X1 | .739a | .098 | -.168 | -.069 | .233 | -.069 | -.186 | -.169 |
| X2 | .098 | .524a | -.234 | -.574 | .734 | -.507 | -.230 | -.519 | |
| X3 | -.168 | -.234 | .538a | -.318 | -.137 | .109 | -.175 | .537 | |
| X4 | -.069 | -.574 | -.318 | .500a | -.753 | .227 | .478 | -.098 | |
| X5 | .233 | .734 | -.137 | -.753 | .386a | -.548 | -.223 | -.117 | |
| X6 | -.069 | -.507 | .109 | .227 | -.548 | .694a | -.160 | -.114 | |
| X7 | -.186 | -.230 | -.175 | .478 | -.223 | -.160 | .622a | -.083 | |
| X8 | -.169 | -.519 | .537 | -.098 | -.117 | -.114 | -.083 | .722a | |
| a. 取样足够度度量 (MSA) |
| 公因子方差 | ||||
|---|---|---|---|---|
| 原始 | 重新标度 | |||
| 初始 | 提取 | 初始 | 提取 | |
| X1 | 2.606 | 2.606 | 1.000 | 1.000 |
| X2 | 154.723 | 154.723 | 1.000 | 1.000 |
| X3 | 9.319 | 9.319 | 1.000 | 1.000 |
| X4 | 15.171 | 15.171 | 1.000 | 1.000 |
| X5 | 8.987 | 8.987 | 1.000 | 1.000 |
| X6 | 9.352 | 9.352 | 1.000 | 1.000 |
| X7 | .747 | .747 | 1.000 | 1.000 |
| X8 | 13.235 | 13.235 | 1.000 | 1.000 |
| 提取方法：主成份分析。 |
| 解释的总方差 | |||||||
|---|---|---|---|---|---|---|---|
| 成份 | 初始特征值a | 提取平方和载入 | |||||
| 合计 | 方差的 % | 累积 % | 合计 | 方差的 % | 累积 % | ||
| 原始 | 1 | 172.376 | 80.497 | 80.497 | 172.376 | 80.497 | 80.497 |
| 2 | 24.787 | 11.575 | 92.072 | 24.787 | 11.575 | 92.072 | |
| 3 | 7.889 | 3.684 | 95.756 | 7.889 | 3.684 | 95.756 | |
| 4 | 3.682 | 1.720 | 97.476 | 3.682 | 1.720 | 97.476 | |
| 5 | 2.504 | 1.169 | 98.645 | 2.504 | 1.169 | 98.645 | |
| 6 | 1.622 | .758 | 99.403 | 1.622 | .758 | 99.403 | |
| 7 | .914 | .427 | 99.830 | .914 | .427 | 99.830 | |
| 8 | .364 | .170 | 100.000 | .364 | .170 | 100.000 | |
| 重新标度 | 1 | 172.376 | 80.497 | 80.497 | 2.755 | 34.433 | 34.433 |
| 2 | 24.787 | 11.575 | 92.072 | 2.319 | 28.992 | 63.425 | |
| 3 | 7.889 | 3.684 | 95.756 | .768 | 9.601 | 73.026 | |
| 4 | 3.682 | 1.720 | 97.476 | .611 | 7.641 | 80.668 | |
| 5 | 2.504 | 1.169 | 98.645 | .625 | 7.818 | 88.485 | |
| 6 | 1.622 | .758 | 99.403 | .318 | 3.976 | 92.461 | |
| 7 | .914 | .427 | 99.830 | .168 | 2.102 | 94.563 | |
| 8 | .364 | .170 | 100.000 | .435 | 5.437 | 100.000 | |
| 提取方法：主成份分析。 | |||||||
| a. 分析协方差矩阵时，初始特征值在整个原始解和重标刻度解中均相同。 |
| 成份矩阵a | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 原始 | 重新标度 | |||||||||||||||
| 成份 | 成份 | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| X1 | .538 | -.376 | -.173 | .395 | 1.172 | .767 | .151 | -.061 | .334 | -.233 | -.107 | .245 | .726 | .475 | .093 | -.038 |
| X2 | 12.415 | -.398 | -.575 | -.072 | -.244 | .071 | .157 | -.029 | .998 | -.032 | -.046 | -.006 | -.020 | .006 | .013 | -.002 |
| X3 | -.063 | 2.279 | -1.772 | .739 | .379 | -.530 | -.095 | -.035 | -.021 | .746 | -.581 | .242 | .124 | -.174 | -.031 | -.011 |
| X4 | 1.673 | 3.336 | .195 | -.957 | .149 | .350 | -.349 | .152 | .429 | .856 | .050 | -.246 | .038 | .090 | -.090 | .039 |
| X5 | -.349 | 2.714 | .966 | .218 | -.169 | -.030 | .691 | -.117 | -.116 | .905 | .322 | .073 | -.056 | -.010 | .230 | -.039 |
| X6 | 2.267 | .792 | 1.218 | 1.333 | -.299 | .208 | -.439 | -.017 | .741 | .259 | .398 | .436 | -.098 | .068 | -.144 | -.005 |
| X7 | .347 | -.241 | .071 | .417 | .083 | -.065 | .238 | .567 | .402 | -.279 | .082 | .482 | .096 | -.075 | .275 | .656 |
| X8 | 3.125 | -.340 | 1.389 | -.245 | .883 | -.759 | -.096 | -.019 | .859 | -.093 | .382 | -.067 | .243 | -.209 | -.026 | -.005 |
| 提取方法 :主成份。 | ||||||||||||||||
| a. 已提取了 8 个成份。 |
| 成份得分系数矩阵a | ||||||||
|---|---|---|---|---|---|---|---|---|
| 成份 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| X1 | .005 | -.024 | -.035 | .173 | .756 | .763 | .266 | -.272 |
| X2 | .896 | -.200 | -.906 | -.242 | -1.211 | .544 | 2.138 | -1.000 |
| X3 | -.001 | .281 | -.686 | .612 | .462 | -.998 | -.317 | -.293 |
| X4 | .038 | .524 | .096 | -1.013 | .231 | .841 | -1.489 | 1.620 |
| X5 | -.006 | .328 | .367 | .177 | -.202 | -.055 | 2.265 | -.961 |
| X6 | .040 | .098 | .472 | 1.107 | -.365 | .391 | -1.469 | -.141 |
| X7 | .002 | -.008 | .008 | .098 | .029 | -.035 | .225 | 1.344 |
| X8 | .066 | -.050 | .640 | -.242 | 1.283 | -1.702 | -.381 | -.187 |
| 提取方法 :主成份。 | ||||||||
| a. 系数已被标准化。 |
| 成份得分协方差矩阵 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 成份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1.000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 |
| 2 | .000 | 1.000 | .000 | .000 | .000 | .000 | .000 | .000 |
| 3 | .000 | .000 | 1.000 | .000 | .000 | .000 | .000 | .000 |
| 4 | .000 | .000 | .000 | 1.000 | .000 | .000 | .000 | .000 |
| 5 | .000 | .000 | .000 | .000 | 1.000 | .000 | .000 | .000 |
| 6 | .000 | .000 | .000 | .000 | .000 | 1.000 | .000 | .000 |
| 7 | .000 | .000 | .000 | .000 | .000 | .000 | 1.000 | .000 |
| 8 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | 1.000 |
| 提取方法 :主成份。 |
四、总结
1、模型求解过程列表表示：
| 主成分 | 特征值 | 贡献率 | 累积贡献率 |
|---|---|---|---|
| 1 | 172.376 | 80.497 | 80.497 |
| 2 | 24.787 | 11.575 | 92.072 |
| 3 | 7.889 | 3.684 | 95.756 |
| 4 | 3.682 | 1.720 | 97.476 |
| 5 | 2.504 | 1.169 | 98.645 |
| 6 | 1.622 | .758 | 99.403 |
| 7 | .914 | .427 | 99.830 |
| 8 | .364 | .170 | 100.000 |
2、由表可知包含原始变量80%的主成分为：
第一主成分的的系数为负数，其余均为正数。因此当较大时，城镇居民的人均烟茶支出和人均衣着商品支出相对较小，而X1: 人均粮食支出 ，X2: 人均副食支出X4: 人均其它副食支出 ，X6: 人均日用品支出，X7: 人均燃料支出 ，X8: 人均非商品支出相对较大；若较小，则反之。
3、按照第一主成分排序、列表，得出结论：
| 省（市、区）编号 | Y1的得分 | 排名 | 省（市、区）编号 | Y1的得分 | 排名 |
|---|---|---|---|---|---|
| 30 | 83.7748 | 1 | 12 | 40.1061 | 16 |
| 29 | 71.5115 | 2 | 16 | 39.2255 | 17 |
| 23 | 59.6109 | 3 | 19 | 38.0799 | 18 |
| 22 | 57.0392 | 4 | 20 | 37.6378 | 19 |
| 21 | 56.4681 | 5 | 11 | 34.3808 | 20 |
| 26 | 55.1969 | 6 | 3 | 33.7994 | 21 |
| 27 | 54.805 | 7 | 10 | 32.9174 | 22 |
| 25 | 49.4952 | 8 | 9 | 32.8944 | 23 |
| 24 | 48.9207 | 9 | 8 | 32.6647 | 24 |
| 18 | 45.1931 | 10 | 4 | 32.5003 | 25 |
| 17 | 44.1456 | 11 | 7 | 23.3607 | 26 |
| 28 | 43.827 | 12 | 6 | 31.8674 | 27 |
| 14 | 42.731 | 13 | 5 | 31.3498 | 28 |
| 13 | 41.4331 | 14 | 2 | 27.8561 | 29 |
| 15 | 41.1138 | 15 | 1 | 27.6086 | 30 |
通过SPSS计算得到解释总方差得到特征值：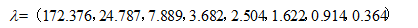
由于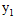
所占贡献率已经高于80%，故取
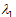，由成分矩阵得到对应的特征向量：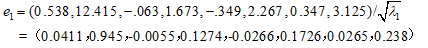
从而求得贡献率达80%的主成分函数：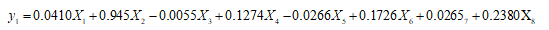
将题目中的数据代入表达式即可得到主成分的排序。
若有收获，就点个赞吧
0 人点赞
