一、任务需求
广告效应:为研究广告的效果,考察4种广告形式:当地报纸(paper)、当地广播(radio)、店内销售员(people)和店内展示(display)的效果。共设有144个销售点,每种广告方式随机地抽取36个销售点记录销售额,分布在6个地区的144个销售点的销售情况生成的数据集。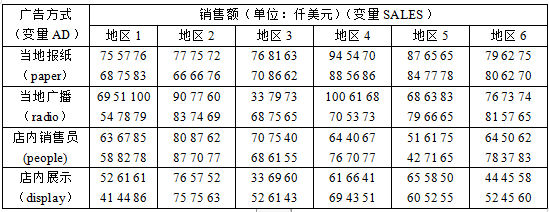
二、算法步骤
1、 用两因素方差分析方法分析销售数据,并指出广告方式和地区对销售量是否有显著性影响(a=0.01,0.10)
通过使用SPSS软件,对上述问题进行了统计分析
| N | ||
|---|---|---|
| 广告方式 | 1 | 36 |
| 2 | 36 | |
| 3 | 36 | |
| 4 | 36 | |
| 地区 | 1 | 24 |
| 2 | 24 | |
| 3 | 24 | |
| 4 | 24 | |
| 5 | 24 | |
| 6 | 24 |
结果分析:
主体间因子:两因素为广告方式和地区。广告方式有四个水平,分别用数字1~4表示当地报纸,当地广播,店内销售员和店内展示;地区有六个水平,分别用数字1~6表示地区1,地区2,地区3,地区4,地区5地区6。
| Descriptive Statistics | ||||
|---|---|---|---|---|
| Dependent Variable:销售额 | ||||
| 广告方式 | 地区 | Mean | Std. Deviation | N |
| 1 | 1 | 72.33 | 8.892 | 6 |
| 2 | 72.00 | 4.940 | 6 | |
| 3 | 73.00 | 9.716 | 6 | |
| 4 | 74.67 | 17.189 | 6 | |
| 5 | 76.00 | 9.295 | 6 | |
| 6 | 71.33 | 8.042 | 6 | |
| Total | 73.22 | 9.734 | 36 | |
| 2 | 1 | 71.83 | 18.126 | 6 |
| 2 | 75.50 | 10.521 | 6 | |
| 3 | 65.00 | 16.236 | 6 | |
| 4 | 70.83 | 15.993 | 6 | |
| 5 | 70.67 | 8.262 | 6 | |
| 6 | 71.00 | 8.602 | 6 | |
| Total | 70.81 | 12.924 | 36 | |
| 3 | 1 | 72.17 | 11.017 | 6 |
| 2 | 77.17 | 9.827 | 6 | |
| 3 | 61.50 | 12.661 | 6 | |
| 4 | 65.67 | 13.545 | 6 | |
| 5 | 60.83 | 12.432 | 6 | |
| 6 | 62.33 | 17.143 | 6 | |
| Total | 66.61 | 13.498 | 36 | |
| 4 | 1 | 57.50 | 16.257 | 6 |
| 2 | 66.33 | 10.463 | 6 | |
| 3 | 53.00 | 13.191 | 6 | |
| 4 | 55.17 | 11.907 | 6 | |
| 5 | 56.67 | 5.502 | 6 | |
| 6 | 50.67 | 7.090 | 6 | |
| Total | 56.56 | 11.619 | 36 | |
| Total | 1 | 68.46 | 14.638 | 24 |
| 2 | 72.75 | 9.597 | 24 | |
| 3 | 63.13 | 14.293 | 24 | |
| 4 | 66.58 | 15.701 | 24 | |
| 5 | 66.04 | 11.630 | 24 | |
| 6 | 63.83 | 13.373 | 24 | |
| Total | 66.80 | 13.511 | 144 |
结果分析:
描述统计:Mean表示两个水平之间的平均值,Std. Deviation表示两个水平之间的标准偏差 ,N表示观测值的个数。例如,第一组数据中表示当两水平为当地报纸与地区1时,销售额的平均值为72.33,标准偏差为8.892,观测值的个数为6。
| Levene’s Test of Equality of Error Variancesa | |||
|---|---|---|---|
| Dependent Variable:销售额 | |||
| F | df1 | df2 | Sig. |
| 1.011 | 23 | 120 | .457 |
| Tests the null hypothesis that the error variance of the dependent variable is equal across groups. | |||
| a. Design: Intercept + 广告方式 + 地区 + 广告方式 * 地区 |
结果分析:
误差方差的齐性检验:统计量F的值为1.011,显著性为0.457,假设的显著性水平为0.01,由于0.457大于0.01,故样本来自总体的方差是相等的。
2、 广告方式(AD)与地区(AREA)之间有无相互作用
| Tests of Between-Subjects Effects | |||||
|---|---|---|---|---|---|
| Dependent Variable:销售额 | |||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
| Corrected Model | 8477.660a | 23 | 368.594 | 2.509 | .001 |
| Intercept | 642535.840 | 1 | 642535.840 | 4374.092 | .000 |
| 广告方式 | 5841.854 | 3 | 1947.285 | 13.256 | .000 |
| 地区 | 1465.951 | 5 | 293.190 | 1.996 | .084 |
| 广告方式 * 地区 | 1169.854 | 15 | 77.990 | .531 | .919 |
| Error | 17627.500 | 120 | 146.896 | ||
| Total | 668641.000 | 144 | |||
| Corrected Total | 26105.160 | 143 | |||
| a. R Squared = .325 (Adjusted R Squared = .195) |
结果分析:
主体间效应的检验:表中得出了不同方差来源的平方和,自由度,均方,F值和P值。
1)显著性水平为0.01
广告方式的显著性水平为0.000,小于0.01,故广告方式对销售额有显著性影响。地区的显著性水平为0.084,大于0.01,故地区对销售额没有显著性影响。广告方式地区的交互效应的显著性水平为0.919,大于0.01,故两个因素的交互效应对销售额没有显著性影响。
2)显著性水平为0.1
广告方式的显著性水平为0.000,小于0.1,故广告方式对销售额有显著性影响。地区的显著性水平为0.084,小于0.1,故地区对销售额有显著性影响。广告方式与地区的交互效应的显著性水平为0.919,大于0.1,故两个因素的交互效应对销售额没有显著性影响。
| Grand Mean | |||
|---|---|---|---|
| Dependent Variable:销售额 | |||
| Mean | Std. Error | 99% Confidence Interval | |
| Lower Bound | Upper Bound | ||
| 66.799 | 1.010 | 64.155 | 69.442 |
| Grand Mean | |||
| Dependent Variable:销售额 | |||
| Mean | Std. Error | 90% Confidence Interval | |
| Lower Bound | Upper Bound | ||
| 66.799 | 1.010 | 65.124 | 68.473 |
结果分析:
1)显著性水平为0.01时,销售额的平均值为66.799,标准误差为1.010。在99%的置信区间里,销售额的上限值为64.155千美元,下限值为69.442千美元。
2)显著性水平为0.1时,销售额的平均值为66.799,标准误差为1.010。在90%的置信区间里,销售额的上限值为64.124千美元,下限值为68.473千美元。
| Multiple Comparisons | ||||||
|---|---|---|---|---|---|---|
| 销售额 LSD |
||||||
| (I) 广告方式 | (J) 广告方式 | Mean Difference (I-J) | Std. Error | Sig. | 99% Confidence Interval | |
| Lower Bound | Upper Bound | |||||
| 1 | 2 | 2.42 | 2.857 | .399 | -5.06 | 9.89 |
| 3 | 6.61 | 2.857 | .022 | -.87 | 14.09 | |
| 4 | 16.67* | 2.857 | .000 | 9.19 | 24.14 | |
| 2 | 1 | -2.42 | 2.857 | .399 | -9.89 | 5.06 |
| 3 | 4.19 | 2.857 | .145 | -3.28 | 11.67 | |
| 4 | 14.25* | 2.857 | .000 | 6.77 | 21.73 | |
| 3 | 1 | -6.61 | 2.857 | .022 | -14.09 | .87 |
| 2 | -4.19 | 2.857 | .145 | -11.67 | 3.28 | |
| 4 | 10.06* | 2.857 | .001 | 2.58 | 17.53 | |
| 4 | 1 | -16.67* | 2.857 | .000 | -24.14 | -9.19 |
| 2 | -14.25* | 2.857 | .000 | -21.73 | -6.77 | |
| 3 | -10.06* | 2.857 | .001 | -17.53 | -2.58 | |
| Based on observed means. The error term is Mean Square(Error) = 146.896. |
||||||
| *. The mean difference is significant at the .01 level. | ||||||
| Multiple Comparisons | ||||||
| 销售额 LSD |
||||||
| (I) 广告方式 | (J) 广告方式 | Mean Difference (I-J) | Std. Error | Sig. | 90% Confidence Interval | |
| Lower Bound | Upper Bound | |||||
| 1 | 2 | 2.42 | 2.857 | .399 | -2.32 | 7.15 |
| 3 | 6.61* | 2.857 | .022 | 1.88 | 11.35 | |
| 4 | 16.67* | 2.857 | .000 | 11.93 | 21.40 | |
| 2 | 1 | -2.42 | 2.857 | .399 | -7.15 | 2.32 |
| 3 | 4.19 | 2.857 | .145 | -.54 | 8.93 | |
| 4 | 14.25* | 2.857 | .000 | 9.51 | 18.99 | |
| 3 | 1 | -6.61* | 2.857 | .022 | -11.35 | -1.88 |
| 2 | -4.19 | 2.857 | .145 | -8.93 | .54 | |
| 4 | 10.06* | 2.857 | .001 | 5.32 | 14.79 | |
| 4 | 1 | -16.67* | 2.857 | .000 | -21.40 | -11.93 |
| 2 | -14.25* | 2.857 | .000 | -18.99 | -9.51 | |
| 3 | -10.06* | 2.857 | .001 | -14.79 | -5.32 | |
| Based on observed means. The error term is Mean Square(Error) = 146.896. |
||||||
| *. The mean difference is significant at the .1 level. |
结果分析:
广告方式对应销售额的多重比较(采用LSD方法):
1)显著性水平为0.01
例如在第一组数据中,在因素广告方式1与广告方式2的作用下,销售额的平均值差值为2.42,标准误差为2.857,显著性水平为0.399,大于0.01,故广告方式1与广告方式2对销售额的影响没用显著差异。
同理可知,广告方式1与4,广告方式2与4,广告方式3与4显著性水平均小于0.01,对销售额的影响有显著差异。广告方式1与3, 广告方式1与2, 广告方式2与3显著性水平均大于0.01,对销售额的影响没用显著差异。
2)显著性水平为0.1
广告方式1与3,广告方式1与4,广告方式2与4,广告方式3与4,显著性水平均小于0.1,对销售额的影响有显著差异。其余两种广告方式的二重组合的显著性水平均大于0.1,对销售额的影响没用显著差异。
| Multiple Comparisons | ||||||
|---|---|---|---|---|---|---|
| 销售额 LSD |
||||||
| (I) 地区 | (J) 地区 | Mean Difference (I-J) | Std. Error | Sig. | 99% Confidence Interval | |
| Lower Bound | Upper Bound | |||||
| 1 | 2 | -4.29 | 3.499 | .222 | -13.45 | 4.87 |
| 3 | 5.33 | 3.499 | .130 | -3.82 | 14.49 | |
| 4 | 1.87 | 3.499 | .593 | -7.28 | 11.03 | |
| 5 | 2.42 | 3.499 | .491 | -6.74 | 11.57 | |
| 6 | 4.63 | 3.499 | .189 | -4.53 | 13.78 | |
| 2 | 1 | 4.29 | 3.499 | .222 | -4.87 | 13.45 |
| 3 | 9.63* | 3.499 | .007 | .47 | 18.78 | |
| 4 | 6.17 | 3.499 | .081 | -2.99 | 15.32 | |
| 5 | 6.71 | 3.499 | .058 | -2.45 | 15.87 | |
| 6 | 8.92 | 3.499 | .012 | -.24 | 18.07 | |
| 3 | 1 | -5.33 | 3.499 | .130 | -14.49 | 3.82 |
| 2 | -9.63* | 3.499 | .007 | -18.78 | -.47 | |
| 4 | -3.46 | 3.499 | .325 | -12.62 | 5.70 | |
| 5 | -2.92 | 3.499 | .406 | -12.07 | 6.24 | |
| 6 | -.71 | 3.499 | .840 | -9.87 | 8.45 | |
| 4 | 1 | -1.87 | 3.499 | .593 | -11.03 | 7.28 |
| 2 | -6.17 | 3.499 | .081 | -15.32 | 2.99 | |
| 3 | 3.46 | 3.499 | .325 | -5.70 | 12.62 | |
| 5 | .54 | 3.499 | .877 | -8.62 | 9.70 | |
| 6 | 2.75 | 3.499 | .433 | -6.41 | 11.91 | |
| 5 | 1 | -2.42 | 3.499 | .491 | -11.57 | 6.74 |
| 2 | -6.71 | 3.499 | .058 | -15.87 | 2.45 | |
| 3 | 2.92 | 3.499 | .406 | -6.24 | 12.07 | |
| 4 | -.54 | 3.499 | .877 | -9.70 | 8.62 | |
| 6 | 2.21 | 3.499 | .529 | -6.95 | 11.37 | |
| 6 | 1 | -4.63 | 3.499 | .189 | -13.78 | 4.53 |
| 2 | -8.92 | 3.499 | .012 | -18.07 | .24 | |
| 3 | .71 | 3.499 | .840 | -8.45 | 9.87 | |
| 4 | -2.75 | 3.499 | .433 | -11.91 | 6.41 | |
| 5 | -2.21 | 3.499 | .529 | -11.37 | 6.95 | |
| Based on observed means. The error term is Mean Square(Error) = 146.896. |
||||||
| *. The mean difference is significant at the .01 level. |
结果分析:
地区对应销售额的多重比较(采用LSD方法):
1) 显著性水平为0.01
例如在第一组数据中,在地区1与地区2的作用下,销售额的平均值差值为-4.29,标准误差为3.499,显著性水平为0.222,大于0.01,故地区1与地区2对销售额的影响没用显著差异。同理可知,地区2与3的显著性水平为0.007,小于0.01,对销售额的影响有显著差异外,其余两个地区的二重组合对销售额的影响均没有显著性差异。
2) 显著性水平为0.1
地区2与3,地区2与4,地区2与5,地区2与6的显著性水平小于0.1, 对销售额的影响有显著差异外,其余两个地区的二重组合对销售额的影响均没有显著性差异。
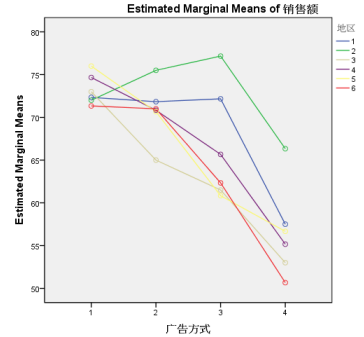
结果分析:
横坐标为广告方式,纵坐标为销售额,用不同颜色的折线图表示不同的地区。
从图中可以看出,当广告方式为1时,各地区销售额的差异较小,其中地区5的销售额最大;当地区为2时,使用广告方式3的销售额最大。
图中存在相交点,表示广告方式与地区之间存在交互效应。例如广告方式3与地区1,2,3,4的组合,广告方式4与地区1,2,3,4的组合,两者对于的销售额之间存在差异,即广告方式与地区之间存在交互效应,但交互效应与销售额的
3、 方差分析表
通过使用SPSS软件得到如下结果:
| 表2.3 方差分析表 | |||||
|---|---|---|---|---|---|
| 方差来源 | 平方和 | 自由度 | 均方 | F值 | p值 |
| 广告方式 | 5841.854 | 3 | 1947.285 | 13.256 | .000 |
| 地区 | 1465.951 | 5 | 293.190 | 1.996 | .084 |
| 广告方式 * 地区 | 1169.854 | 15 | 77.990 | .531 | .919 |
| 误差 | 17627.500 | 120 | 146.896 | ||
| 总和 | 668641.000 | 144 |
结果分析:
当假定显著性水平为0.01时,广告方式对销售额有显著性影响,地区对销售额没有显著性影响;当假定显著性水平为0.1时,广告方式和地区对销售额均有显著性影响。无论显著性水平为0.01还是0.1,交互效应与销售额的影响无显著性差异。

