一、任务需求
考察1985年至2000年全国6个价格指数:商品零售价格指数X1,居民消费价格指数X2,城市居民消费价格指数X3,农村居民消费价格指数X4,农产品收购价格指数X5,农村工业品零售价格指数X6,观测数据如下表所示。
首先选取了1985年至2000年这16个年份,以全国6个价值指数作为指标对各年份进行评价。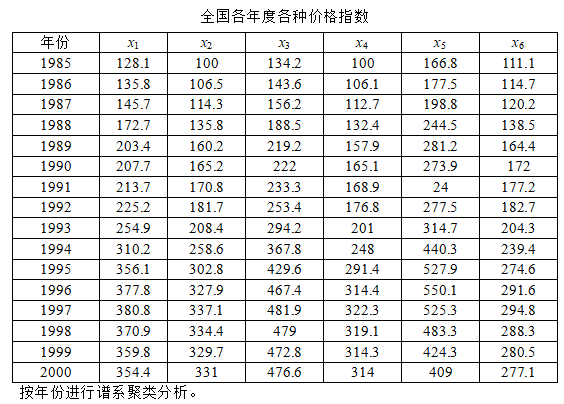
二、聚类分析
聚类分析将个体或对象分类,使得同一类中的对象之间的相似性比与其他类的对象的相似性更强。其目的在于使类内对象的同质性最大化和类与类间对象的异质性最大化。
聚类与分类的不同在于,聚类所要求划分的类是未知的。聚类是将数据分类到不同的类或者簇这样的一个过程,所以同一个簇中的对象有很大的相似性,而不同簇间的对象有很大的相异性。从统计学的观点看,聚类分析是通过数据建模简化数据的一种方法。传统的统计聚类分析方法包括系统聚类法、K-均值聚类法、快速聚类法等。
谱系聚类法
谱系聚类法(系统聚类)的合并算法通过计算两类数据点间的距离,对最为接近的两类数据点进行组合,并反复迭代这一过程,直到将所有数据点合成一类,并生成聚类谱系图。
1) 最长距离法:也称为最远邻元素聚类,用两个类别中各个事物(个案)之间最长的那个距离来表示两个类别之间的距离。
2) 组间联接:用两个类别间各个事物(个案)两两之间距离的平均值来表示两个类别之间的距离,这是SPSS默认的方法,也是最为稳健的聚类方法。
3) 组内联接:除了考虑上面组间联接的距离之外,还需要综合考虑类别内部在合并之前的类别距离。也就是充分考虑所有数据点之间的距离关系。
谱系聚类法的基本原理
设有个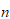 样品的
样品的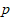 元观测数据组成的一个数字矩阵如下:
元观测数据组成的一个数字矩阵如下: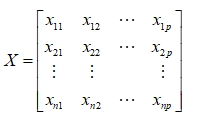
其中每一行代表一个样品,每一列代表一个指标,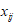 表示第
表示第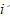 个样品关于第
个样品关于第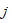 个指标的观测值。在样品之间定义距离,在指标之间定义相似系数,样品之间的相似系数刻画指标之间的相似度。将样品按照相似度逐一归类,关系密切的聚集到较小的一类,关系疏远的聚集到较大的一类。设
个指标的观测值。在样品之间定义距离,在指标之间定义相似系数,样品之间的相似系数刻画指标之间的相似度。将样品按照相似度逐一归类,关系密切的聚集到较小的一类,关系疏远的聚集到较大的一类。设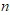 个样品的
个样品的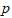 元观测数据:
元观测数据:
此时每个样品可看作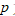 元空间的一个点,每两个点之间的距离记为
元空间的一个点,每两个点之间的距离记为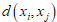 满足条件:
满足条件: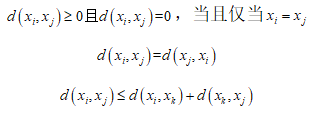
欧式距离表示为: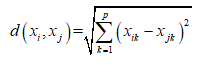
其算法流程如下:
a) 将每个对象看作一类,计算两两之间的最小距离;
b) 将距离最小的两个类合并成一个新类;
c) 重新计算新类与所有类之间的距离;
d) 重复二三两步,直到所有类最后合并成一类;
e) 结束
三、聚类模型
3.1 符号约定
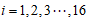 表示1895年至2000年这16个年份;
表示1895年至2000年这16个年份;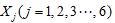 表示指标变量商品零售价格指数
表示指标变量商品零售价格指数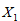 ,居民消费价格指数
,居民消费价格指数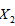 ,城市居民消费价格指数
,城市居民消费价格指数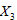 ,农村居民消费价格指数
,农村居民消费价格指数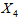 ,农产品收购价格指数
,农产品收购价格指数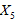 ,农村工业品零售价格指数
,农村工业品零售价格指数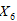 ;
;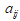 表示第
表示第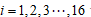 个年份第个指标变量的取值;
个年份第个指标变量的取值;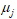 表示第
表示第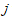 个指标变量的样本均值;
个指标变量的样本均值;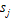 表示第
表示第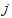 个指标变量的样本标准差;
个指标变量的样本标准差;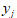 表示标准化指标变量。
表示标准化指标变量。
3.2 基本假设
1)假设图表中的数据经过完全统计;
2)假设本题中考虑的指标变量相互之间无联系。3.4 模型的建立
1)首先,将数据进行标准化处理可得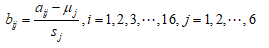
其中,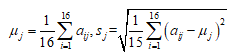 ;
;
标准化指标变量为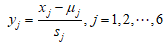 ;
;
2)接着,计算两点之间的距离,并构造距离矩阵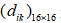 采用欧几里得距离
采用欧几里得距离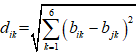 ;
;
3)然后,构造出16个类,且每个类只包含一个样本点,每类的平台高度(树状图横坐标的值,实际上是距离值)为0;
4)合并距离最近的两类为新类,且以这两类之间的距离值作为聚类图的平台高度;
5)最后,绘制出聚类图,选着所需要的决定类的个数和类。3.5 模型的求解
使用的是SPSS处理,具体方法为:
在SPSS中导入数据表格,选择菜单分析>>分类>>系统聚类命令,将待聚类变量选入到变量框中,然后选择需要使用的方法:
方法>>最长距离法>>图>>勾选谱系图>>确认
方法>>组类连接法>>图>>勾选谱系图>>确认
四、结果分析
4.1 最长距离法
聚类表
| 聚类表 | ||||||
|---|---|---|---|---|---|---|
| 阶 | 群集组合 | 系数 | 首次出现阶群集 | 下一阶 | ||
| 群集 1 | 群集 2 | 群集 1 | 群集 2 | |||
| 1 | 5 | 6 | 214.220 | 0 | 0 | 6 |
| 2 | 15 | 16 | 291.030 | 0 | 0 | 11 |
| 3 | 1 | 2 | 354.560 | 0 | 0 | 5 |
| 4 | 12 | 13 | 991.580 | 0 | 0 | 7 |
| 5 | 1 | 3 | 2266.350 | 3 | 0 | 9 |
| 6 | 5 | 8 | 2812.920 | 1 | 0 | 10 |
| 7 | 12 | 14 | 4719.640 | 4 | 0 | 8 |
| 8 | 11 | 12 | 6602.100 | 0 | 7 | 11 |
| 9 | 1 | 4 | 14057.100 | 5 | 0 | 13 |
| 10 | 5 | 9 | 15172.360 | 6 | 0 | 14 |
| 11 | 11 | 15 | 20761.430 | 8 | 2 | 12 |
| 12 | 10 | 11 | 39980.070 | 0 | 11 | 15 |
| 13 | 1 | 7 | 56363.230 | 9 | 0 | 14 |
| 14 | 1 | 5 | 94190.450 | 13 | 10 | 15 |
| 15 | 1 | 10 | 452654.220 | 14 | 12 | 0 |
上图是聚类表,在聚类表中列出了变量逐步聚类的过程。聚类表中将
1985~2000年编号为为1~16,上图的聚类群集表呈现出了变量被逐步聚合起来的过程:第一行的是5和6,即1989和1990年被首先聚合,其距离系数为214.220,是最小的。然后是第二行,15和16,1999年和2000年被聚合。其它行的解释以此类推。
聚类成员
| 群集成员 | |
|---|---|
| 案例 | 3 群集 |
| 1:1985 | 1 |
| 2:1986 | 1 |
| 3:1987 | 1 |
| 4:1988 | 1 |
| 5:1989 | 2 |
| 6:1990 | 2 |
| 7:1991 | 1 |
| 8:1992 | 2 |
| 9:1993 | 2 |
| 10:1994 | 3 |
| 11:1995 | 3 |
| 12:1996 | 3 |
| 13:1997 | 3 |
| 14:1998 | 3 |
| 15:1999 | 3 |
| 16:2000 | 3 |
使用最长距离法将年份分成了3类,其中的颜色代表不同的类别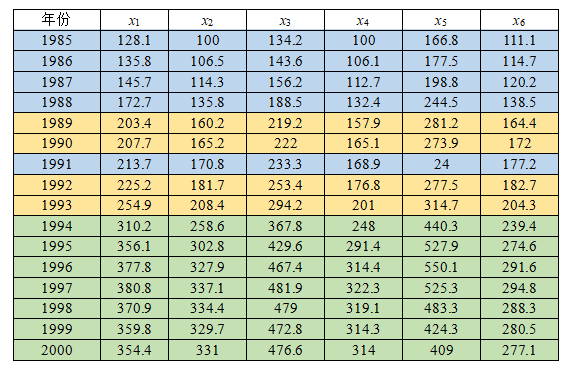
冰挂图
在冰挂图中,每个待分类变量占据一列,在列与列之间预留分隔列,系统借助分隔列的填充长度说明相邻两列之间的聚类关系。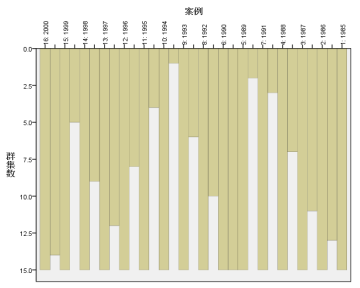
在上图中,1998年和1999年之间的分隔列基本被填满了,说明这两个变量是非常密切的,属于比较早被聚合的列。而1993年1994年之间几乎为空白,说明这两列之间距离较远,是最后才聚合的。
树状图(谱系图)
谱系图显示了上方聚类步骤的综合情况。我们以距离5.1为切点,将16个年份分类为3大类。然后根据每个年份的特点对它们进行描述。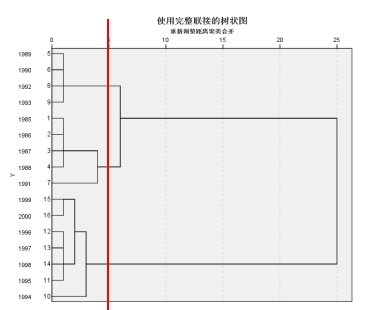
注:使用的是spss处理,具体方法为:分析>>分类>>系统聚类>>方法>>最长距离法>>图>>勾选谱系图>>确认
谱系图显示了上方聚类步骤的综合情况。我们以距离5.0为切点,将16个年份分类为3大类。然后根据每个年份的特点对它们进行描述。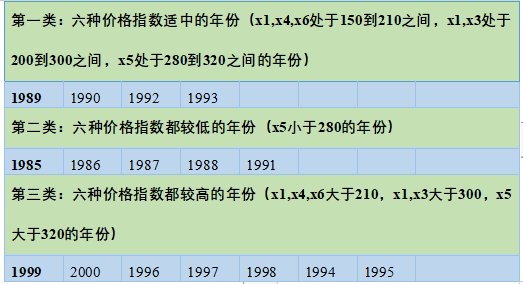
4.2 类平均距离法(组类连接)
聚类表
| 聚类表 | ||||||
|---|---|---|---|---|---|---|
| 阶 | 群集组合 | 系数 | 首次出现阶群集 | 下一阶 | ||
| 群集 1 | 群集 2 | 群集 1 | 群集 2 | |||
| 1 | 5 | 6 | 214.220 | 0 | 0 | 6 |
| 2 | 15 | 16 | 291.030 | 0 | 0 | 10 |
| 3 | 1 | 2 | 354.560 | 0 | 0 | 5 |
| 4 | 12 | 13 | 991.580 | 0 | 0 | 7 |
| 5 | 1 | 3 | 1155.340 | 3 | 0 | 13 |
| 6 | 5 | 8 | 1618.647 | 1 | 0 | 9 |
| 7 | 12 | 14 | 2547.140 | 4 | 0 | 8 |
| 8 | 11 | 12 | 3995.930 | 0 | 7 | 10 |
| 9 | 4 | 5 | 5060.135 | 0 | 6 | 11 |
| 10 | 11 | 15 | 8554.579 | 8 | 2 | 12 |
| 11 | 4 | 9 | 10169.622 | 9 | 0 | 13 |
| 12 | 10 | 11 | 14629.483 | 0 | 10 | 15 |
| 13 | 1 | 4 | 24590.770 | 5 | 11 | 14 |
| 14 | 1 | 7 | 32905.558 | 13 | 0 | 15 |
| 15 | 1 | 10 | 143174.142 | 14 | 12 | 0 |
聚类成员
| 群集成员 | |
|---|---|
| 案例 | 3 群集 |
| 1:1985 | 1 |
| 2:1986 | 1 |
| 3:1987 | 1 |
| 4:1988 | 1 |
| 5:1989 | 1 |
| 6:1990 | 1 |
| 7:1991 | 2 |
| 8:1992 | 1 |
| 9:1993 | 1 |
| 10:1994 | 3 |
| 11:1995 | 3 |
| 12:1996 | 3 |
| 13:1997 | 3 |
| 14:1998 | 3 |
| 15:1999 | 3 |
| 16:2000 | 3 |
使用类平均距离法将年份分成3类,其中不同的颜色代表不同的类别。
| 年份 | _x_1 | _x_2 | _x_3 | _x_4 | _x_5 | _x_6 |
|---|---|---|---|---|---|---|
| 1985 | 128.1 | 100 | 134.2 | 100 | 166.8 | 111.1 |
| 1986 | 135.8 | 106.5 | 143.6 | 106.1 | 177.5 | 114.7 |
| 1987 | 145.7 | 114.3 | 156.2 | 112.7 | 198.8 | 120.2 |
| 1988 | 172.7 | 135.8 | 188.5 | 132.4 | 244.5 | 138.5 |
| 1989 | 203.4 | 160.2 | 219.2 | 157.9 | 281.2 | 164.4 |
| 1990 | 207.7 | 165.2 | 222 | 165.1 | 273.9 | 172 |
| 1991 | 213.7 | 170.8 | 233.3 | 168.9 | 24 | 177.2 |
| 1992 | 225.2 | 181.7 | 253.4 | 176.8 | 277.5 | 182.7 |
| 1993 | 254.9 | 208.4 | 294.2 | 201 | 314.7 | 204.3 |
| 1994 | 310.2 | 258.6 | 367.8 | 248 | 440.3 | 239.4 |
| 1995 | 356.1 | 302.8 | 429.6 | 291.4 | 527.9 | 274.6 |
| 1996 | 377.8 | 327.9 | 467.4 | 314.4 | 550.1 | 291.6 |
| 1997 | 380.8 | 337.1 | 481.9 | 322.3 | 525.3 | 294.8 |
| 1998 | 370.9 | 334.4 | 479 | 319.1 | 483.3 | 288.3 |
| 1999 | 359.8 | 329.7 | 472.8 | 314.3 | 424.3 | 280.5 |
| 2000 | 354.4 | 331 | 476.6 | 314 | 409 | 277.1 |
冰挂图
在冰挂图中,每个待分类变量占据一列,在列与列之间预留分隔列,系统借助分隔列的填充长度说明相邻两列之间的聚类关系。在上图中,1998年和1999年之间的分隔列基本被填满了,说明这两个变量是非常密切的,属于比较早被聚合的列。而1993年1994年之间几乎为空白,说明这两列之间距离较远,是最后才聚合的。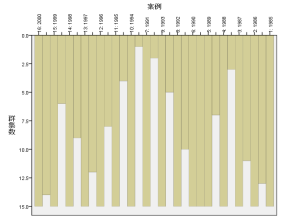
树状图(谱系图)
谱系图显示了上方聚类步骤的综合情况。我们以距离5.1为切点,将16个年份分类为3大类。然后根据每个年份的特点对它们进行描述。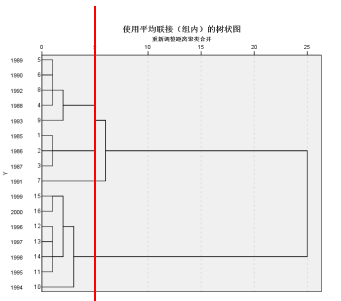
注:使用的是spss处理,具体方法为:分析>>分类>>系统聚类>>方法>>组间>>图>>勾选谱系图>>确认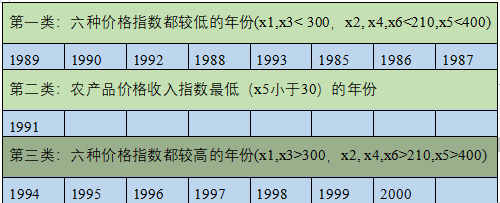
五、总结
| 类别 | 最长距离法 |
|---|---|
| 1 | 1989 1990 1992 1993 |
| 2 | 1985 1986 1987 1988 1991 |
| 3 | 1994 1995 1996 1997 1998 1999 2000 |
使用最长距离法聚类时,
第一类:价格指数x1,x4,x6处于150到210之间,x1,x3处于200到300之间,x5处于280到320之间的年份,为六种价格指数适中的年份;
第二类:x5小于280的年份,为六种价格指数都较低的年份;
第三类x1,x4,x6大于210,x1,x3大于300,x5大于320的年份,为六种价格指数都较高的年份。
| 类别 | 类平均距离法 |
|---|---|
| 1 | 1985 1986 1987 1988 1989 1990 1992 1993 |
| 2 | 1991 |
| 3 | 1994 1995 1996 1997 1998 1999 2000 |
使用类平均距离法聚类时,
第一类:价格指数x1,x3< 300,x2, x4,x6<210,x5<400,为六种价格指数都较低的年份;
第二类:价格指数x5小于30,为农产品价格收入指数最低的年份;
第三类:价格指数x1,x3>300,x2, x4,x6>210,x5>400,为六种价格指数都较高的年份。
上述结果与不同年份的经济发展水平,国家出台的相关方针政策有关。随时间的推移,价格指数总体上呈现上升的趋势,一段时间内的各年份聚为一类,故年份的分类也相对比较集中。

