一、任务需求
为制订企业的长期市场发展计划,根据某汽车企业1988—2001年的汽车销售量数据(见表1.1),预测出至2011年的汽车销量。
二、分析目标
该案例的研究目标旨在预测出至2011年的汽车销量,即未来十年的汽车销量,需考虑如下制约因素:
1)可用信息量少
仅14个年度销量的数据用于预测,并且除了销量这一信息外无其他可用信息进行分析,所以最后的预测模型的准确度就不会很高,即预测值的区间估计值很宽,并且该值会随着预测年份的增加而出现失去实际意义范围的预测。
2)未来趋势的变化
市场的瞬息万变以及中国飞速发展的工业意味着,即便有上百个数据,十年时间广度太大,再精准的模型也无法预测在大时间跨度下,且有社会、经济影响下的变化趋势。
所以,要预测2-3年内的汽车销量应为该案例更为合适的研究目标。首先进行数据序列趋势的观察,然后按照相应的趋势进行分析建模,最终给出预测结果。
三、数据准备
由于本数据较简单,因此数据理解的重点可放在两变量间数据关联趋势的了解上,首先使用散点图对数据的变化规律进行观察,步骤如下:
1.选择“图形”——“图标构建程序”。
2.将散点图图标拖入画布。
3.将year拖入X轴框,sales拖入Y轴框。
4.确定。
汽车销量的散点图如下: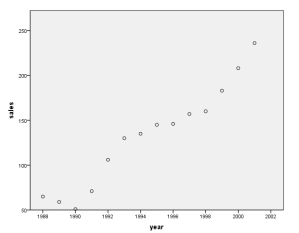
由图可以看出,1988-1992年的数据出现异常,故在后面建模时将其删除,不再进入后续分析,只采用1993-2001年的数据进行建模。观察1993—2001年的销量变化,可以看到呈现出加速上升的曲线趋势,所有可以反映该趋势的曲线模型均在考虑之列。因此,这里可以考虑拟合3种曲线模型。
1) 二次方曲线:
2) 三次方曲线: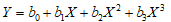
3) 指数曲线:
其中拟合优度较高的模型将用于随后的预测。另外,由于相应模型中存在自变量的高次项或指数项,直接使用年代作为自变量纳入模型将产生数值很大的平方、立方项,这虽然不影响模型精度,但会严重影响方程的可读性。因此我们将为年代产生一个新的序列变量,并将它作为自变量纳入模型。
四、数据分析
4.1线性回归
4.1.1曲线直线化拟合
这里采用比较简单的曲线直线化拟合操作,即直接拟合形式的方程,随后的操作是将time、time2两个变量同时纳入方程,直接进行模型的参数估计,具体操作如下:
(1)“分析”→“回归”→“线性”。
(2)将总信心指数选入“因变量”列表框,将年龄选入“自变量”列表框。
(3) 确定。
线性回归对话框如下: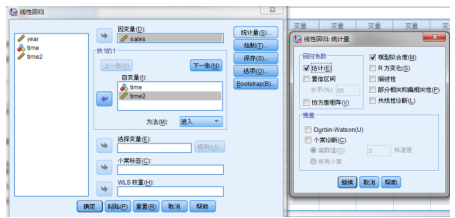
4.1.2 结果分析
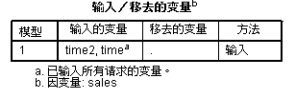
对模型中各个自变量纳入模型情况进行汇总,可以看到进入模型的有两个变量,将所有自变量都放入模型中。筛选自变量的方法有很多种,不同的情况可以选择不同的筛选方法。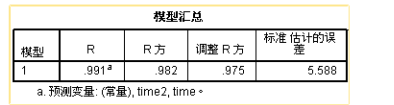
模型R方值为0.982,即拟合的模型决定系数高达98.2%,time,time2可以解释sales的98.2%变化原因,拟合效果应当是非常不错的。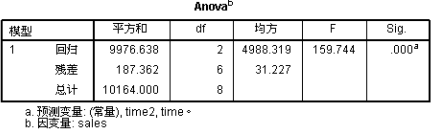
方差分析的结果F的值为159.744,P值小于0.05,所以该模型具有统计意义。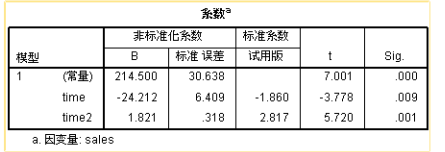
该表给出了回归方程中常数项、回归系数的估计值和检验结果,可见常数项=138.976,两个回归系数分别为-5.998和 1.821,则可以写出回归方程如下:
上述回归方程告诉我们,当time=0,即时间为1993-1=1992年时,销量的模型估计值为138.976,显然这个数值和实际情况差得有点远,因为1993年之前的数据趋势并不服从现在拟合的模型,所以这个估计值没有实际意义。同时销量和时间的一次项负相关,和时间的二次项正相关。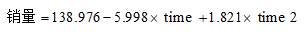
4.1.3 模型拟合效果的判断
1、残差的独立性检验
这可以使用统计量子对话框中的Durbin-Watson检验复选框来进行。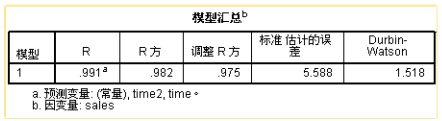
Durbin-Watson统计量的输出1.518,该统计量的取值在0~4之间,意味着独立性应当没有大的问题。
2、残差分析的图形观察
这可以在绘制子对话框中完成:在“绘制”子对话框中,选中“直方图”和“正态概率图”复选框。
从输出的残差直方图和P-P图可以看出,模型的残差较好地服从正态分布,没有明显偏离正态性假设。当然,由于本案例的样本量很少,上述两个图形工具内实际考察价值不大。
3、绘制残差序列图
如果模型的拟合效果好,则残差序列在整个时间范围内应当落在0附近,对于近期的残差波动尤其应当如此,且其残差方差应当在整个时间范围内保持恒定。具体操作如下:
(1)在“保存”子对话框中,选中“标准化残差”复选框。
(2)确定。
(3)依次单击“分析”→“预测”→“序列图”。
(4)变量框:选入ZRE_1。
(5)时间轴标签框:选入 year。
(6)确定。
残差的序列图如下: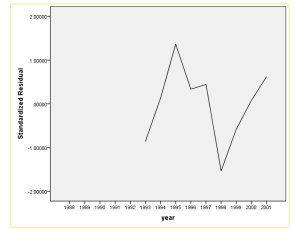
从图中可见,在整个时间段中,标化残差均在0上下波动,且波动范围没有超出±2,没有发现明显方差不齐或者强影响点的线索。
4、存储预测值和区间估计值
本例需要预测区间和预测值,具体操作如下:
(1)在数据集中新增三条记录,变量id分别等于10、11和 12。
(2)重复执行“回归”对话框。
(3)“保存”子对话框:选中“未标化预测值”、“单值预测区间”两个复选框。
4.2 曲线估计
4.2.1.用曲线估计过程同时拟合多个曲线模型
具体操作如下:
(1)依次单击“分析”→“回归”→“曲线估计”。
(2)“因变量”列表框: sales。
(3)“自变量”列表框: time。
(4)模型:选中二次项、立方和指数分布。
(5)选中“显示ANOVA表格”复选框。
(6)确定。
“曲线估计”对话框如下: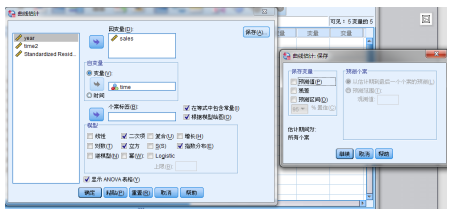
4.2.2结果分析
分析结果中的主要部分如下表所示。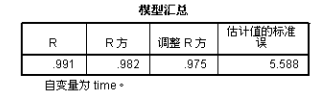
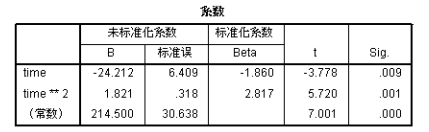
首先输出的是二次方曲线模型的分析结果,从中可见模型的确定系数为0.982,time 的一次方和二次方回归系数分别为-5.998和1.821,显然和上一节手工进行变量变换后所得到的分析结果完全相同。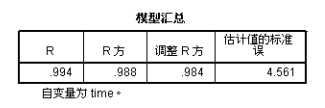
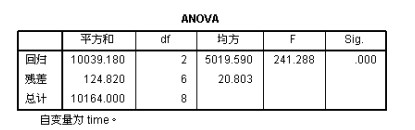
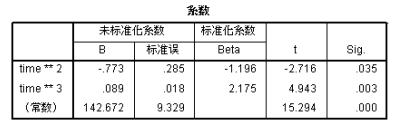
上述三个表为三次方曲线的分析结果,可见在增加了一个三次项之后,模型的决定系数从98.2%上升到了99.4%,调整决定系数也有所上升,这说明新的三次项的增加的确有助于预测效果上升。可以写出方程模型如下: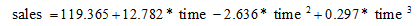
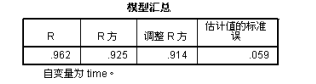
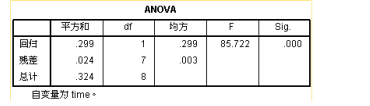
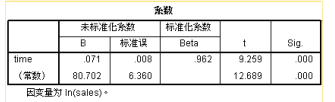
述三个表为为指数曲线模型的数据结果,其决定系数为0.925,显然低于前两个模型。相应的模型表达式如下:
分析结果中最后输出的是实测值和模型预测值的曲线图,从图8.6中可以很明显地看到,指数模型的拟合效果明显差于二次方和三次方模型。后两者的预测值均和实测值非常接近,相比之下,二次方曲线在1997年前后的拟合效果稍差一些。三条拟合曲线的比较如下: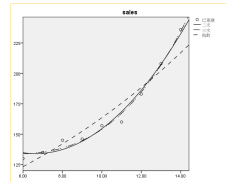
由图可以看出,指数模型的拟合效果明显差于二次方和三次方模型。二次方曲线相较三次方曲线在1997年前后的拟合效果稍差一些。
4.2.3模型拟合效果的判断
1、存储残差值
通过对曲线图以及决定系数的观察,下面考虑使用更加专业的指标对此进行判断,以便从中挑选出最优模型用于随后的预测工作。为此先将模型的残差存为新变量供分析中使用,新增操作如下。
(1)进入“保存”子对话框。
(2)“保存变量”框:选中“残差”。
(3)继续。
再次运行曲线拟合过程,此时会生成ERR_1~ERR_3共3个新变量,分别代表二次、三次和指数模型的误差项。为便于观察,将它们的变量名标签分别改为二次方程、三次方程和指数方程。
2、观察模型误差项的序列图
首先绘制3个模型误差项的序列图(如图4.2.11所示),以观察随着年代的变化,相应预测误差的变动趋势,操作如下。
(1)依次单击“分析”→“预测”→“序列图”。
(2)“变量”框:选入ERR_1~ERR_3。
(3)“时间轴标签”列表框:选入 year。
(4)确定。
模型误差的序列图如下:
从图中可得,指数方程的预测误差一直较大,特别是从1998年到2001年,预测误差由负急剧转正,表明此时模型曲线和实际数据的变动趋势完全不一致,显然该模型不适合于预测。从近几年的数据来看,二次方曲线的误差在从1998年以后也出现了一定的变动趋势,而三次方曲线则较紧密地围绕零点上下波动,由于这些数据点处于序列末端,其预测的准确性更为重要,因此选择三次方模型进行预测。
3、模型的预测
根据上面的讨论,我们已经确定应当使用三次方模型进行预测,并且预测的长度在3年以内比较恰当。为此我们采取和线性回归中相同的操作:在数据集中新增三条记录,变量id分别等于10、11和12,然后在曲线拟合过程中进行操作。
(1)依次单击“分析”→“回归”→“曲线估计”。
(2)“因变量”列表框: sales。
(3)“自变量”列表框:time。
(4)模型:选中“立方”。
(5)“保存”子对话框。
(6)“保存变量”:选中“预测值”和“预测区间”。
(7)确定。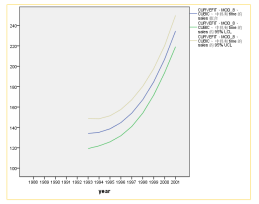
4.3利用非线性回归进行拟合
4.3.1构建分段回归模型
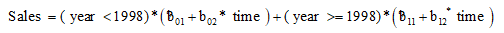
非线性回归模型中可以直接对该分段模型进行拟合,具体如下:
逻辑表达式根据year 的取值是否符合要求得出逻辑结果为0或1,从而实现了分段模型的要求。SPSS中的操作如下,图1.9所示为非线性回归过程设置对话框,表1.15~表1.18为分析输出结果。
(1)依次单击“分析”→“回归”→“非线性”。
(2)“因变量”列表框: sales。
(3)“自变量”列表框:输入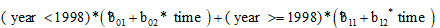
(4)参数:在子对话框中分别将b01、b02、b11和 b12的初始值设为1。
(5)确定。
4.3.2结果分析
迭代历史记录如下:
以上输出为迭代过程记录,观察残差SS的变化。随着迭代的进行,残差SS变得越来越小,即模型无法解释的变异部分越来越少。但这一过程不是无限进行下去,当进行了2步迭代后,残差SS 以及各参数的估计值均稳定下来,模型达到收敛标准。 参数估计值如下: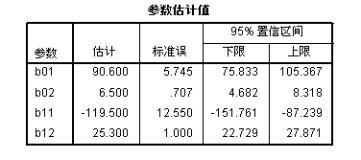
由表可得模型方程如下: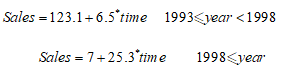
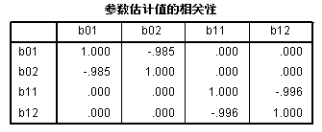
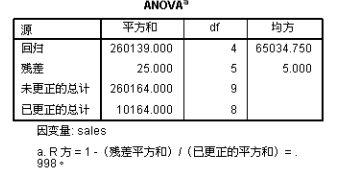
参数估计值的相关性对模型进行近似方差分析的结果,相应的原假设为:所拟合的模型对因变量的预测无贡献。由于这里进行的是非线性回归,方差分析的F值和Р值只有参考意义,因此结果中并不给出,用户可以手工计算。显然,最终的Р值远小于0.05,拒绝原假设,可以认为模型对因变量的预测是有作用的。
4.4不同模型的效果的比较
前面用非线性回归的方法得到了模型表达式的估计值,也给出了销量的预测值。为了直观地对两个模型进行比较,这里存储了相应模型的预测值,并且绘制相应的序列图,操作如下。
(1)进入“保存”子对话框。
(2)选中“预测值”。
(3)确定。
(4)依次单击“分析”→“预测”→“序列图”。
(5)“变量”列表框:选入三次方曲线的预测值FIT1、LCL_1、UCL_1,以及非线性模型的预测值 PRED。
(6)“时间轴标签”列表框:选入year。
(7)确定。
预测值的序列图如下: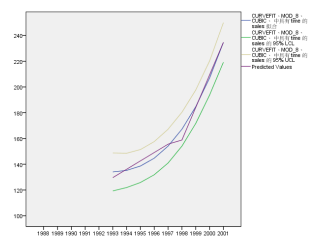
若将三次方曲线预测结果和分段回归模型的预测结果相比较,可以发现三次方曲线的预测值更快速,很快与分段模型的预测结果拉开了距离,由于我们预期2001年中国经济会走上一个比较顺畅的发展阶段,因此更倾向于对销售量进行偏高的预估,因此,三次方结果曲线更合适。
五、总结
在案例基于所有可用的历史销售数据,对未来一定时期内的汽车年销量进行了预测。分析结果显示,过去几年间销量呈加速上升的曲线趋势,通过对二次曲线、三次曲线和指数曲线的拟合,发现三次曲线对历史数据的拟合效果最好。
另一方面,基于2000年之后宏观经济走势可能会进入一个新的上升周期的判断,认为汽车销量应当倾向于比较乐观,因此也倾向于使用上升速度更快的结果。基于上述分析,最终按照三次曲线的趋势进行了未来3年的销量预测,并给出了相应的销量预测区间。
同时,对具体案例还需要具体分析,充分利用专业知识及其相关背景信息,对外部信息有选择性地加以利用,以便得出最佳的预测结果。

