应用预测建模3：衡量回归模型的效果

这一篇以理论内容为主。

我们做好了一个回归模型，那么该如何评价其效果呢？

模型效果的定量度量

当结果是数值时，描述预测能力最常用的指标是均方根误差（root mean square， RMSE），RMSE是MSE（均方误差）的平方根，MSE的计算方法时将残差（实际值减去预测值）平方、求和然后取平均。RMSE可解释为残差距离0的远近，或者实际值和预测值之间的平均距离。

另一个常用的度量是决定系数R2为0.8，可理解为：模型可解释结果变量总变异的80%。可通过先计算实际值和预测值的相关系数，然后平方即可得决定系数。需要注意，R^2是相关性的度量，不是准确性的度量！**

方差-偏差的权衡

对于建立的模型的来说，我们希望它能对新的数据作出很好的预测，但是往往我们的模型在测试集中的表现非常好，但是在新的数据中的表现却很差，这就是方差-偏差问题。

模型对于测试集表现非常棒，就是说偏差非常小，但是偏差越小，方差就会越大，也就是对于新的数据的预测能力越差，也就是存在过拟合问题！

一般来说，复杂的模型通常有着很高的方差，这会导致过拟合。另一方面，简单的模型通常会拟合不足（具有较高的偏差）

使用caret包计算R^2和RMSE

准备数据：

observed <- c(0.22, 0.83, -0.12, 0.89, -0.23, -1.3, -0.15, -1.4,
              0.62, 0.99, -0.18, 0.32, 0.34, -0.3, 0.04, -0.87,
              0.55, -1.3, -1.15, 0.2)
predicted <- c(0.24, 0.78, -0.66, 0.53, 0.70, -0.75, -0.41, -0.43, 
               0.49, 0.79, -1.19, 0.06, 0.75, -0.07, 0.43, -0.42,
               -0.25, -0.64, -1.26, -0.07)

计算残差：

residualValues <- observed - predicted
summary(residualValues)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -0.9700 -0.4200  0.0800 -0.0310  0.2625  1.0100

简单画图看一下：

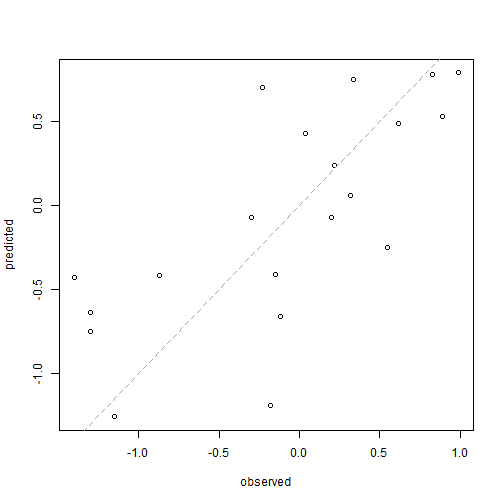
axisRange <- extendrange(c(observed, predicted))
plot(observed, predicted)
abline(0, 1, col = "darkgrey", lty =2)

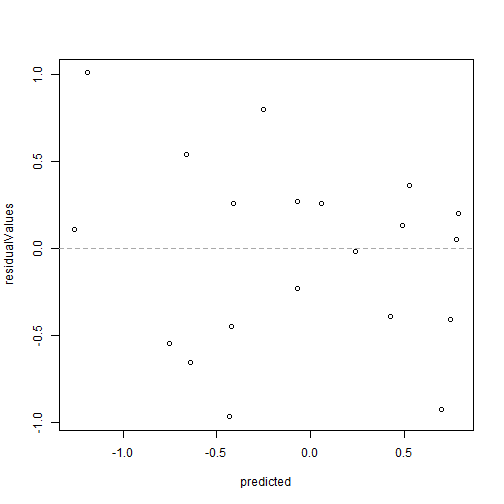
plot(predicted, residualValues)
abline(h = 0, col = "darkgrey", lty = 2)

计算：

library(caret)
## 载入需要的程辑包：lattice
## 载入需要的程辑包：ggplot2
R2(predicted, observed)
## [1] 0.5170123
RMSE(predicted, observed)
## [1] 0.5234883