前言

参数估计，是统计推断的一种。根据从总体中抽取的随机样本来估计总体分布中未知参数的过程。从估计形式看，区分为点估计和区间估计；从构造估计量的方法讲，有矩法估计、最小二乘估计、似然估计、贝叶斯估计等。
要处理两个问题：

1. 求出未知参数的估计量；
2. 在一定信度（可靠程度）下指出所求的估计量的精度。

信度一般用概率表示，如可信程度为95%；精度用估计量与被估参数（或待估参数）之间的接近程度或误差来度量。
本文主要是简单记录求置信区间所用到的python代码～

代码

1、导入数据

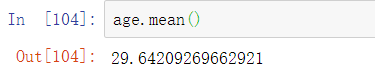
import pandas as pd
import numpy as np
from scipy import stats
path = 'D:\数据\data\data.xlsx'
data = pd.read_excel(path)
age = data['Age']
age.mean()

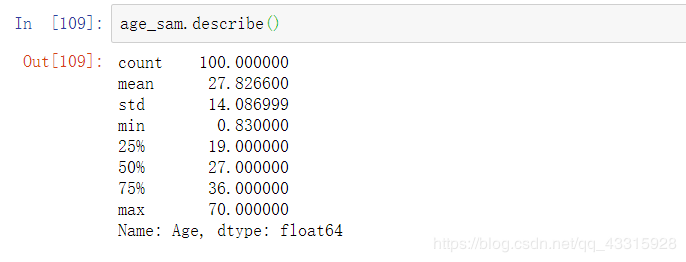
# 抽取100个样本
age_sam = age.sample(100)
x1 = age_sam.mean()
age_sam.describe()

2、 计算置信区间

1. pandas.std()默认是除以n-1，即是无偏大，如果想和numpy.std() 一样有偏，需要加上参数 doff=0，即pandas(doff-0)；DataFrame的describ()中就包含有std()；
2. numpy.std() 求标准差的时候默认是除以n的，即是有偏大，np.std() 无偏样本标准差方式为加入参数 doff=1；

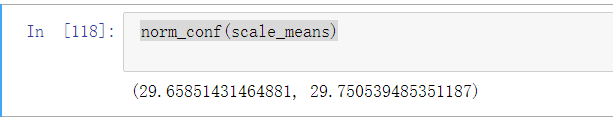
# 正态分布下的置信区间
def norm_conf (data,confidence=0.95):
    # https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html
    sample_mean = np.mean(data)
    sample_std = np.std(data,ddof=1)
    sample_size = len(data)
    conf_intveral = scipy.stats.norm.interval(confidence, loc=sample_mean, scale=sample_std)
    print(conf_intveral)
norm_conf(scale_means)

# T分布下的置信区间
def ttest_conf (data,confidence=0.95):
    sample_mean = np.mean(data)
    sample_std = np.std(data,ddof=1)
    sample_size = len(data)
    conf_intveral = scipy.stats.t.interval(confidence,df = (sample_size-1) , loc=sample_mean, scale=sample_std)
    print(conf_intveral)
ttest_conf(scale_means)

3、重复抽取数据

scale_means = []
for _ in range(1000):
   scale_sample = age.sample(100, replace=True)
   mean = scale_sample.mean()
   scale_means.append(mean)
norm_conf(scale_means)

ttest_conf(scale_means)

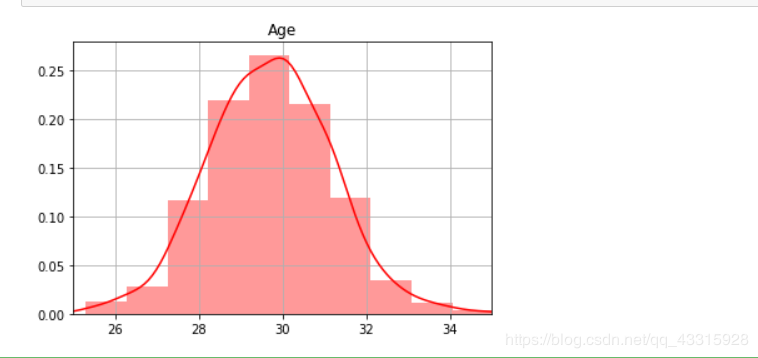
4、绘制数据

import seaborn as sns 
from matplotlib import pyplot as plt
sns.set_palette("hls") #设置所有图的颜色，使用hls色彩空间
sns.distplot(scale_means,color="r",bins=10,kde=True)
plt.title('Age')
plt.xlim(25,35)
plt.grid(True)
plt.show()