空间变换器网络教程

译者：冯宝宝

作者: Ghassen HAMROUNI

https://pytorch.org/tutorials/_images/FSeq.png
在本教程中，您将学习如何使用称为空间变换器网络的视觉注意机制来扩充您的网络。你可以在 DeepMind paper阅读有关空间变换器网络的更多内容。

空间变换器网络是对任何空间变换的差异化关注的概括。空间变换器网络(简称STN）允许神经网络学习如何在输入图像上执行空间变换，以增强模型的几何不变性。例如，它可以裁剪感兴趣的区域，缩放并校正图像的方向。它可能是一种有用的机制，因为CNN对于旋转和缩放以及更一般的仿射变换并不是不变的。
关于STN的最棒的事情之一是能够简单地将其插入任何现有的CNN，只需很少的修改。 

  1. # License: BSD
  2. # 作者: Ghassen Hamrouni
  4. from __future__ import print_function  
  5. import torch  
  6. import torch.nn as nn  
  7. import torch.nn.functional as F  
  8. import torch.optim as optim  
  9. import torchvision  
  10. from torchvision import datasets, transforms  
  11. import matplotlib.pyplot as plt  
  12. import numpy as np  
  14. plt.ion()   # 交互模式

加载数据

在这篇文章中，我们尝试了经典的MNIST数据集。使用标准卷积网络增强空间变换器网络。 

  1. device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
  3. # Training dataset
  4. train_loader = torch.utils.data.DataLoader(
  5.     datasets.MNIST(root='.', train=True, download=True,
  6.                    transform=transforms.Compose([
  7.                        transforms.ToTensor(),
  8.                        transforms.Normalize((0.1307,), (0.3081,))
  9.                    ])), batch_size=64, shuffle=True, num_workers=4)
  10. # Test dataset
  11. test_loader = torch.utils.data.DataLoader(
  12.     datasets.MNIST(root='.', train=False, transform=transforms.Compose([
  13.         transforms.ToTensor(),
  14.         transforms.Normalize((0.1307,), (0.3081,))
  15.     ])), batch_size=64, shuffle=True, num_workers=4)

输出:

  1. Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ./MNIST/raw/train-images-idx3-ubyte.gz
  2. Extracting ./MNIST/raw/train-images-idx3-ubyte.gz
  3. Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ./MNIST/raw/train-labels-idx1-ubyte.gz
  4. Extracting ./MNIST/raw/train-labels-idx1-ubyte.gz
  5. Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ./MNIST/raw/t10k-images-idx3-ubyte.gz
  6. Extracting ./MNIST/raw/t10k-images-idx3-ubyte.gz
  7. Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ./MNIST/raw/t10k-labels-idx1-ubyte.gz
  8. Extracting ./MNIST/raw/t10k-labels-idx1-ubyte.gz
  9. Processing...
  10. Done!

空间变换器网络叙述

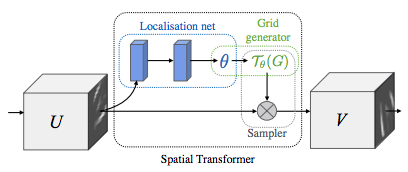
空间变换器网络归结为三个主要组成部分：

  • 本地网络(Localisation Network）是常规CNN，其对变换参数进行回归。不会从该数据集中明确地学习转换，而是网络自动学习增强全局准确性的空间变换。
  • 网格生成器( Grid Genator)在输入图像中生成与输出图像中的每个像素相对应的坐标网格。
  • 采样器(Sampler）使用变换的参数并将其应用于输入图像。

https://pytorch.org/tutorials/_images/stn-arch.png

笔记

我们使用最新版本的Pytorch，它应该包含affine_grid和grid_sample模块。 

  1. class Net(nn.Module):
  2.     def __init__(self):
  3.         super(Net, self).__init__()
  4.         self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
  5.         self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
  6.         self.conv2_drop = nn.Dropout2d()
  7.         self.fc1 = nn.Linear(320, 50)
  8.         self.fc2 = nn.Linear(50, 10)
  10.         # Spatial transformer localization-network
  11.         self.localization = nn.Sequential(
  12.             nn.Conv2d(1, 8, kernel_size=7),
  13.             nn.MaxPool2d(2, stride=2),
  14.             nn.ReLU(True),
  15.             nn.Conv2d(8, 10, kernel_size=5),
  16.             nn.MaxPool2d(2, stride=2),
  17.             nn.ReLU(True)
  18.         )
  20.         # Regressor for the 3 * 2 affine matrix
  21.         self.fc_loc = nn.Sequential(
  22.             nn.Linear(10 * 3 * 3, 32),
  23.             nn.ReLU(True),
  24.             nn.Linear(32, 3 * 2)
  25.         )
  27.         # Initialize the weights/bias with identity transformation
  28.         self.fc_loc[2].weight.data.zero_()
  29.         self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
  31.     # Spatial transformer network forward function
  32.     def stn(self, x):
  33.         xs = self.localization(x)
  34.         xs = xs.view(-1, 10 * 3 * 3)
  35.         theta = self.fc_loc(xs)
  36.         theta = theta.view(-1, 2, 3)
  38.         grid = F.affine_grid(theta, x.size())
  39.         x = F.grid_sample(x, grid)
  41.         return x
  43.     def forward(self, x):
  44.         # transform the input
  45.         x = self.stn(x)
  47.         # Perform the usual forward pass
  48.         x = F.relu(F.max_pool2d(self.conv1(x), 2))
  49.         x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
  50.         x = x.view(-1, 320)
  51.         x = F.relu(self.fc1(x))
  52.         x = F.dropout(x, training=self.training)
  53.         x = self.fc2(x)
  54.         return F.log_softmax(x, dim=1)
  56. model = Net().to(device)

训练模型

现在我们使用SGD(随机梯度下降）算法来训练模型。网络正在以有监督的方式学习分类任务。同时，该模型以端到端的方式自动学习STN。 

  1. optimizer = optim.SGD(model.parameters(), lr=0.01)
  3. def train(epoch):
  4.     model.train()
  5.     for batch_idx, (data, target) in enumerate(train_loader):
  6.         data, target = data.to(device), target.to(device)
  8.         optimizer.zero_grad()
  9.         output = model(data)
  10.         loss = F.nll_loss(output, target)
  11.         loss.backward()
  12.         optimizer.step()
  13.         if batch_idx % 500 == 0:
  14.             print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
  15.                 epoch, batch_idx * len(data), len(train_loader.dataset),
  16.                 100. * batch_idx / len(train_loader), loss.item()))
  17. #
  18. # A simple test procedure to measure STN the performances on MNIST.
  19. #
  21. def test():
  22.     with torch.no_grad():
  23.         model.eval()
  24.         test_loss = 0
  25.         correct = 0
  26.         for data, target in test_loader:
  27.             data, target = data.to(device), target.to(device)
  28.             output = model(data)
  30.             # sum up batch loss
  31.             test_loss += F.nll_loss(output, target, size_average=False).item()
  32.             # get the index of the max log-probability
  33.             pred = output.max(1, keepdim=True)[1]
  34.             correct += pred.eq(target.view_as(pred)).sum().item()
  36.         test_loss /= len(test_loader.dataset)
  37.         print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'
  38.               .format(test_loss, correct, len(test_loader.dataset),
  39.                       100. * correct / len(test_loader.dataset)))

可视化STN结果

现在，我们将检查我们学习的视觉注意机制的结果。
我们定义了一个小辅助函数，以便在训练时可视化变换。 

  1. def convert_image_np(inp):
  2.     """Convert a Tensor to numpy image."""
  3.     inp = inp.numpy().transpose((1, 2, 0))
  4.     mean = np.array([0.485, 0.456, 0.406])
  5.     std = np.array([0.229, 0.224, 0.225])
  6.     inp = std * inp + mean
  7.     inp = np.clip(inp, 0, 1)
  8.     return inp
  10. # We want to visualize the output of the spatial transformers layer
  11. # after the training, we visualize a batch of input images and
  12. # the corresponding transformed batch using STN.
  14. def visualize_stn():
  15.     with torch.no_grad():
  16.         # Get a batch of training data
  17.         data = next(iter(test_loader))[0].to(device)
  19.         input_tensor = data.cpu()
  20.         transformed_input_tensor = model.stn(data).cpu()
  22.         in_grid = convert_image_np(
  23.             torchvision.utils.make_grid(input_tensor))
  25.         out_grid = convert_image_np(
  26.             torchvision.utils.make_grid(transformed_input_tensor))
  28.         # Plot the results side-by-side
  29.         f, axarr = plt.subplots(1, 2)
  30.         axarr[0].imshow(in_grid)
  31.         axarr[0].set_title('Dataset Images')
  33.         axarr[1].imshow(out_grid)
  34.         axarr[1].set_title('Transformed Images')
  36. for epoch in range(1, 20 + 1):
  37.     train(epoch)
  38.     test()
  40. # Visualize the STN transformation on some input batch
  41. visualize_stn()
  43. plt.ioff()
  44. plt.show()

https://pytorch.org/tutorials/_images/sphx_glr_spatial_transformer_tutorial_001.png

输出： 

  1. Train Epoch: 1 [0/60000 (0%)]   Loss: 2.336866
  2. Train Epoch: 1 [32000/60000 (53%)]      Loss: 0.841600
  4. Test set: Average loss: 0.2624, Accuracy: 9212/10000 (92%)
  6. Train Epoch: 2 [0/60000 (0%)]   Loss: 0.527656
  7. Train Epoch: 2 [32000/60000 (53%)]      Loss: 0.428908
  9. Test set: Average loss: 0.1176, Accuracy: 9632/10000 (96%)
  11. Train Epoch: 3 [0/60000 (0%)]   Loss: 0.305364
  12. Train Epoch: 3 [32000/60000 (53%)]      Loss: 0.263615
  14. Test set: Average loss: 0.1099, Accuracy: 9677/10000 (97%)
  16. Train Epoch: 4 [0/60000 (0%)]   Loss: 0.169776
  17. Train Epoch: 4 [32000/60000 (53%)]      Loss: 0.408683
  19. Test set: Average loss: 0.0861, Accuracy: 9734/10000 (97%)
  21. Train Epoch: 5 [0/60000 (0%)]   Loss: 0.286635
  22. Train Epoch: 5 [32000/60000 (53%)]      Loss: 0.122162
  24. Test set: Average loss: 0.0817, Accuracy: 9743/10000 (97%)
  26. Train Epoch: 6 [0/60000 (0%)]   Loss: 0.331074
  27. Train Epoch: 6 [32000/60000 (53%)]      Loss: 0.126413
  29. Test set: Average loss: 0.0589, Accuracy: 9822/10000 (98%)
  31. Train Epoch: 7 [0/60000 (0%)]   Loss: 0.109780
  32. Train Epoch: 7 [32000/60000 (53%)]      Loss: 0.172199
  34. Test set: Average loss: 0.0629, Accuracy: 9814/10000 (98%)
  36. Train Epoch: 8 [0/60000 (0%)]   Loss: 0.078934
  37. Train Epoch: 8 [32000/60000 (53%)]      Loss: 0.156452
  39. Test set: Average loss: 0.0563, Accuracy: 9839/10000 (98%)
  41. Train Epoch: 9 [0/60000 (0%)]   Loss: 0.063500
  42. Train Epoch: 9 [32000/60000 (53%)]      Loss: 0.186023
  44. Test set: Average loss: 0.0713, Accuracy: 9799/10000 (98%)
  46. Train Epoch: 10 [0/60000 (0%)]  Loss: 0.199808
  47. Train Epoch: 10 [32000/60000 (53%)]     Loss: 0.083502
  49. Test set: Average loss: 0.0528, Accuracy: 9850/10000 (98%)
  51. Train Epoch: 11 [0/60000 (0%)]  Loss: 0.092909
  52. Train Epoch: 11 [32000/60000 (53%)]     Loss: 0.204410
  54. Test set: Average loss: 0.0471, Accuracy: 9857/10000 (99%)
  56. Train Epoch: 12 [0/60000 (0%)]  Loss: 0.078322
  57. Train Epoch: 12 [32000/60000 (53%)]     Loss: 0.041391
  59. Test set: Average loss: 0.0634, Accuracy: 9796/10000 (98%)
  61. Train Epoch: 13 [0/60000 (0%)]  Loss: 0.061228
  62. Train Epoch: 13 [32000/60000 (53%)]     Loss: 0.137952
  64. Test set: Average loss: 0.0654, Accuracy: 9802/10000 (98%)
  66. Train Epoch: 14 [0/60000 (0%)]  Loss: 0.068635
  67. Train Epoch: 14 [32000/60000 (53%)]     Loss: 0.084583
  69. Test set: Average loss: 0.0515, Accuracy: 9853/10000 (99%)
  71. Train Epoch: 15 [0/60000 (0%)]  Loss: 0.263158
  72. Train Epoch: 15 [32000/60000 (53%)]     Loss: 0.127036
  74. Test set: Average loss: 0.0493, Accuracy: 9851/10000 (99%)
  76. Train Epoch: 16 [0/60000 (0%)]  Loss: 0.083642
  77. Train Epoch: 16 [32000/60000 (53%)]     Loss: 0.028274
  79. Test set: Average loss: 0.0461, Accuracy: 9867/10000 (99%)
  81. Train Epoch: 17 [0/60000 (0%)]  Loss: 0.076734
  82. Train Epoch: 17 [32000/60000 (53%)]     Loss: 0.034796
  84. Test set: Average loss: 0.0409, Accuracy: 9864/10000 (99%)
  86. Train Epoch: 18 [0/60000 (0%)]  Loss: 0.122501
  87. Train Epoch: 18 [32000/60000 (53%)]     Loss: 0.152187
  89. Test set: Average loss: 0.0474, Accuracy: 9860/10000 (99%)
  91. Train Epoch: 19 [0/60000 (0%)]  Loss: 0.050512
  92. Train Epoch: 19 [32000/60000 (53%)]     Loss: 0.270055
  94. Test set: Average loss: 0.0416, Accuracy: 9878/10000 (99%)
  96. Train Epoch: 20 [0/60000 (0%)]  Loss: 0.073357
  97. Train Epoch: 20 [32000/60000 (53%)]     Loss: 0.017542
  99. Test set: Average loss: 0.0713, Accuracy: 9816/10000 (98%)