求解
- 方法一、暴力解法
- 解法二、动态规划

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

求解

方法一、暴力解法

比较容易想到的是用“暴力解法”做，即穷举所有的子区间。思路虽然简单，但是写好暴力解法也不是一件容易的事情。

使用双层循环，穷举所有的子区间；
然后再对子区间内的所有元素求和；
时间复杂度是立方级别的。

参考代码 1：
这里要注意一些边界条件：

变量 i 表示结尾的那个索引；
变量 j 表示从索引 0 依次向前走；

class Solution {
private:
    int sumOfArray(vector<int> &nums, int left, int right) {
        int res = 0;
        for (int i = left; i <= right; ++i) {
            res += nums[i];
        }
        return res;
    }
public:
    int maxSubArray(vector<int> &nums) {
        int size = nums.size();
        int res = INT_MIN;
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j <= i; ++j) {
                int sum = sumOfArray(nums, j, i);
                res = max(res, sum);
            }
        }
        return res;
    }
};

复杂度分析：

时间复杂度：O(N^3)，这里 N 为数组的长度。
空间复杂度：O(1)。

提交以后发现“超时”，有两种情况：

程序当中写了“死循环”；
代码“正确”，复杂度较高，本解法属于这种情况。

优化：
事实上，上面的代码有一些重复计算。这是因为相同前缀的区间求和，可以通过类似“状态转移”的方法得到。
例如：计算子区间 [1, 4] 的和可以在计算子区间 [1, 3] 的基础上，再加上 nums[4] 得到。
因此，只需要枚举子序的左端点，然后再扫描右端点，就可以减少一个级别的复杂度。

参考代码 2：

class Solution1 {
    public int maxSubArray(int[] nums) {
        int res = nums[0];
        // 寻找以 i 为索引的元素作为左侧的所有子序列中的最大值
        for (int i = 0; i < nums.length ; i++) {
            int sum = 0;
            for (int j = i; j < nums.length; j++) {
                sum += nums[j];
                res = Math.max(sum, res);
            }
        }
        return res;
    }
    public static void main(String[] args)
    {
        // [4,-1,2,1] has the largest sum = 6.
        System.out.println((new Solution1()).maxSubArray(new int[]{-2,1,-3,4,-1,2,1,-5,4}));  
    }
}

复杂度分析：**
时间复杂度：O(N^2)
空间复杂度：O(1)

其实这道题是一个非常经典的动态规划问题。

该问题最早于 1977 年提出，但是直到 1984 年才被 Jay Kadane 发现了线性时间的最优解法。

解法二、动态规划

利用空间换时间

按照排列组合的数学算法，9 个数字，以第 i 个数字结尾的串，有 i 种组合，一共有45个组合( 😜day3-Maximum Subarray - 图2 )，如果有n个数字，时间复杂度是 😜day3-Maximum Subarray - 图3 ，这样的时间复杂度是明显不能接受的。

我们把目光落到动态规划上面来，首先需要把这个问题分解成最优子问题来解。最主要的思路就是将上面的45个组合进行
，分解成数量较少的几个子问题。在这里我们一共有9个数字，顺理成章的我们把组合分解成9个小组的组合。

这道题让求最大子数组之和，并且要用两种方法来解，分别是 O(n) 的解法，还有用分治法 Divide and Conquer Approach，这个解法的时间复杂度是 O(nlgn)。
那就先来看 O(n) 的解法，定义两个变量 res 和 curSum，其中 res 保存最终要返回的结果，即最大的子数组之和，curSum 初始值为0，每遍历一个数字 num，比较 curSum + num 和 num 中的较大值存入 curSum，然后再把 res 和 curSum 中的较大值存入 res，以此类推直到遍历完整个数组，可得到最大子数组的值存在 res 中，代码如下：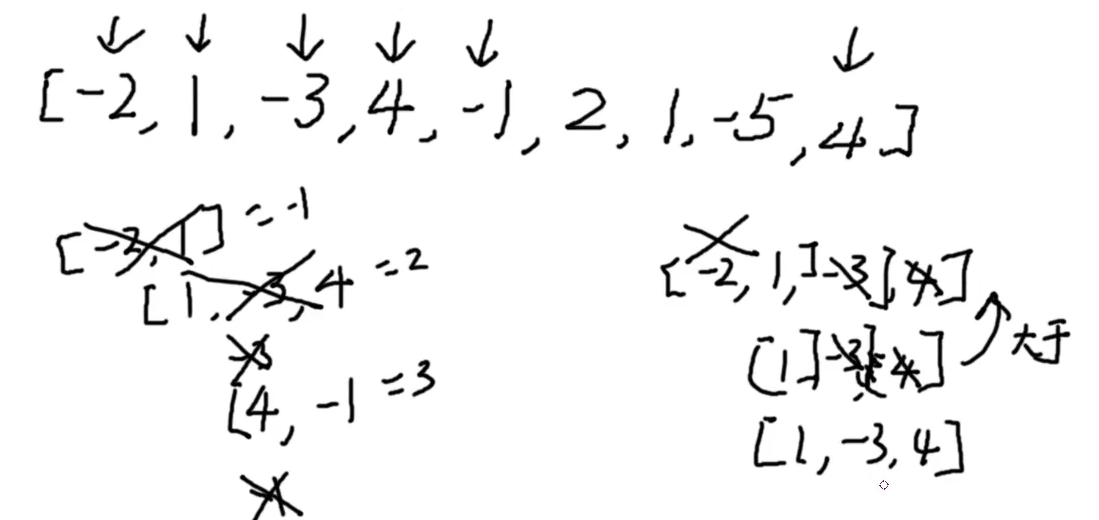

class Solution {
    public int maxSubArray(int[] nums) {
        int res = Integer.MIN_VALUE, curSum = 0;
        for (int num : nums) {
            curSum = Math.max(curSum + num, num);
            res = Math.max(res, curSum);
        }
        return res;
    }
}

题目还要求我们用分治法 Divide and Conquer Approach 来解，这个分治法的思想就类似于二分搜索法，需要把数组一分为二，分别找出左边和右边的最大子数组之和，然后还要从中间开始向左右分别扫描，求出的最大值分别和左右两边得出的最大值相比较取最大的那一个，代码如下：

public class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 0) return 0;
        return helper(nums, 0, nums.length - 1);
    }
    public int helper(int[] nums, int left, int right) {
        if (left >= right) return nums[left];
        int mid = left + (right - left) / 2;
        int lmax = helper(nums, left, mid - 1);
        int rmax = helper(nums, mid + 1, right);
        int mmax = nums[mid], t = mmax;
        for (int i = mid - 1; i >= left; --i) {
            t += nums[i];
            mmax = Math.max(mmax, t);
        }
        t = mmax;
        for (int i = mid + 1; i <= right; ++i) {
            t += nums[i];
            mmax = Math.max(mmax, t);
        }
        return Math.max(mmax, Math.max(lmax, rmax));
    }
}