✔ 164. Maximum Gap(最大间距)(桶)

题目链接

题目

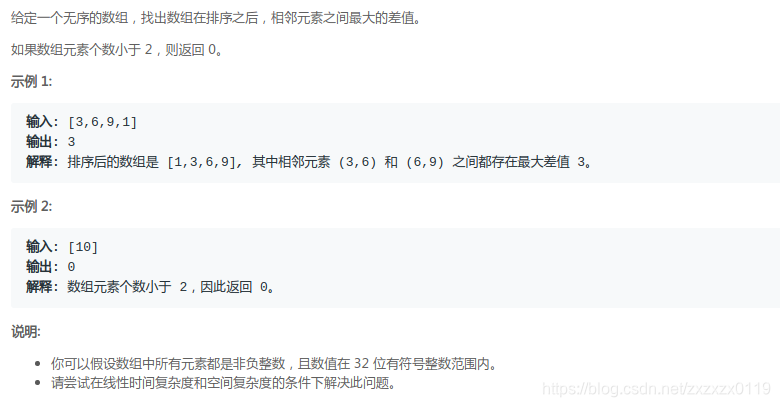
解析

桶排序思想和相关实现可以看下这篇博客。
思路:

• 先找到数组的最大值和最小值，记为max和min；
• 假设数组长度为N，准备N+1个桶，把max放在N+1号桶，nums中在[min,max)范围上的数放在1~N号桶中，对于1 ~ N号桶的每一个桶来说，负责的区间大小(桶的容量)为(max - min)/N；

  首先，要知道很关键一点：相邻的最大差值一定不小于该数组的最大值减去最小值除以间隔个数(相邻元素平均差距)，取上界。即 ，这里的 N 是数组的元素个数，N-1为间隔个数。很明显

  (或者我们可以用反证法证明，如果小于，会怎么呢？比如 [1, 2, 5], 利用上式得 gap = 2. 如果假设相邻间隔最大为 1，那必然不能组成以上数组! )

• 注意每个桶中存的不是很多的数，只存三个值，是否有数进入过这个桶，以及所有进入这个桶的数的最大值、最小值；
• 最后计算相邻非空桶的间距 (当前桶的min 减去前一个桶的max) ，然后记录更新最大值；

比如下面的例子:

注意不一定就是空桶两侧的非空桶的答案: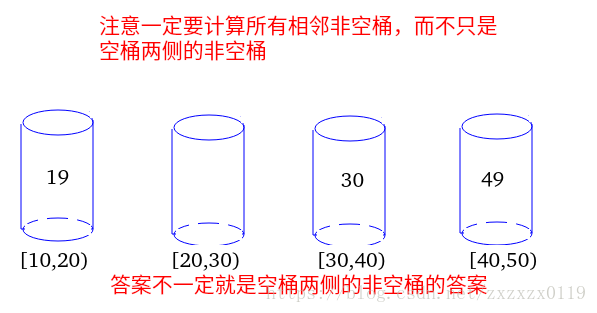

class Solution {
    public int mapToBucket(long num, long len, long min, long max) {
        return (int) ((num - min) * len / (max - min));
    }
    public int maximumGap(int[] nums) {
        if (nums == null || nums.length < 2)
            return 0;
        int len = nums.length;
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; i++) {
            min = nums[i] < min ? nums[i] : min;
            max = nums[i] > max ? nums[i] : max;
        }
        if (max == min)
            return 0;
        boolean[] hasNum = new boolean[len + 1];
        int[] mins = new int[len + 1];
        int[] maxs = new int[len + 1];
        for (int i = 0; i < nums.length; i++) {
            int bid = mapToBucket(nums[i], len, min, max);
            mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i];
            maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i];
            hasNum[bid] = true;
        }
        int res = 0, preMax = maxs[0]; 
        for (int i = 1; i <= len; i++) {
            if (hasNum[i]) { 
                res = Math.max(res, mins[i] - preMax);
                preMax = maxs[i];
            }
        }
        return res;
    }
}