算法设计与实验二：钢条切割

title: 算法设计与分析实验二：钢条切割问题
date: 2021-05-19

钢条切割问题

1.问题描述
设有一个长度为 L 的钢条，在钢条上标有 n 个位置点（p1,p2,…,pn）。现在需要按钢条上标注的位置将钢条切割为 n+1 段，假定每次切割所需要的花费与所切割的钢条长度成正比。请编写⼀个算法，能够确定⼀个切割方案，使切割的总花费最小。
数据规模：
⚫ 2 ≤ L ≤ 105
⚫ 1 ≤ n ≤ 200
⚫ 1 ≤ 𝑝𝑖 < 𝐿
2.题目分析
用数组表示一钢条。0、1、2、…、len为坐标，设x_i为一切割点且位于坐标i处。切断x_i后，钢条分为左右两段子钢条，原钢条是最大的子钢条。现设钢条的左右端点为x_0,x_len，对于中间钢条，切掉一次后也变成了端点钢条。则左右两子钢条可以记作(x_0,x_i),( x_i,x_len)。按照这种记法，原钢条可以记为(x_0,x_len)。

要切下一段钢条需要一次或两次切割：切掉端点处的钢条需要一次；切掉中间的钢条需要两次。现按照三元组的记法来确定一段切割：记三元组M_mn=(x_m,x_i,x_n)为切割mn,0<m<i<n<len。其中x_i为切割点，则一个三元组中有正整数个切割点。以二元数组（矩阵）的形式建立备忘录记录任意三元组最小总花费。

总花费是指将该三元组切割到不可再分的所有花费。由于给定三元组的端点就确定了本次切割花费，故定义总花费的概念。钢条的花费与长度成正比，则不妨取二者相等。由此有某一三元组M_mn的总花费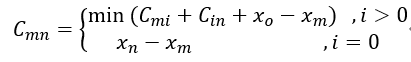

由此递推式可以求出元钢条的最小花费。
3.程序设计
现设计程序：
设钢条长度为barlen。经实际编程后发现对于钢条只需要知道长度。
可用一数组x存储切割点。设切割点共有xnum个，则x长度应为xnum+2（两端视为切割点）。
输入后动态生成两数组，先初始化再逐渐优化。
值得注意的是：
输入的xnum要加2，因为把端点也看做切割点。
memo只需要存储切割点即可，而不需存储其他点。
lowestCost函数中应采用步长而不是循环每一行每一列。这是因为大步长的结果需要用到小步长的结果。
4.代码
代码如下：

#include"iostream"
#include"algorithm"
#define INF 100000000
using namespace std;
int num; int barlenn;
int main()
{
    int lowestCost(int m, int n, int* &x, int xlen, int** &memo);
    int* x;//切割点数组
    int** memo;//备忘录矩阵
    int barnum, xnum;
    cin >> barnum >> xnum;
    int xlen = xnum + 2;
    num = xlen;
    int barlen = barnum + 1;//应有长度
    x = new int[xlen];
    x[0] = 0; x[xlen - 1] = barnum;
    for (int i = 1; i < xlen - 1; i++)
    {
        cin >> x[i];
    }
    //切割点排序
    sort(x, x + xlen);//注意排序函数用法
    //初始化备忘录
    memo = new int*[xlen];
    for (int i = 0; i < xlen; i++)
        memo[i] = new int[xlen];
    for (int i = 0; i < xlen; i++)
    {
        for (int j = 0; j < xlen; j++)
            memo[i][j] = INF;
    }
    int result;
    result = lowestCost(0, xlen - 1, x, xlen, memo);
    cout << result << endl;
    //释放指针数组
    if (x)
        delete[] x;
    if (memo)
    {
        for (int i = 0; i < xnum; i++)
        {
            if (memo[i])
                delete[] memo[i];
        }
        delete[] memo;
    }
    return 0;
}
int lowestCost(int m, int n, int* &x, int xlen, int** &memo)
{
    for (int i = 0; i < xlen; i++)
    {
        memo[i][i] = 0;
        if (i + 1 < xlen)
        {
            memo[i][i+1] = 0;
        }
        if (i + 2 < xlen)
        {
            memo[i][i+2] = x[i + 2] - x[i];
        }
    }
    int temp;
    //应采用步长
    for (int step = 3; step <= x[xlen - 1]; step++)//注意边界
    {
        for (int m = 0; m < xlen; m++)
        {
            if (m + step <= xlen - 1)
            {
                for (int i = m + 1; i < m + step; i++)
                {
                    temp = memo[m][i] + memo[i][m + step] + x[m + step] - x[m];
                    if (temp < memo[m][m + step])
                    {
                        memo[m][m + step] = temp;
                    }
                }
            }
        }
    }
    return memo[m][n];
}

5.运行结果

附：输入文件
链接：https://pan.baidu.com/s/1Ii5jg1b36Zy76xFbox-7pw
提取码：umao