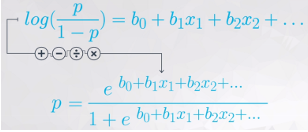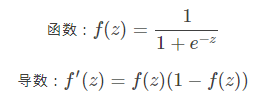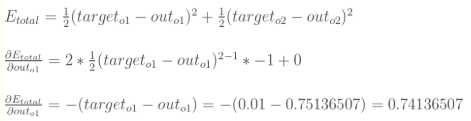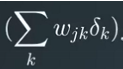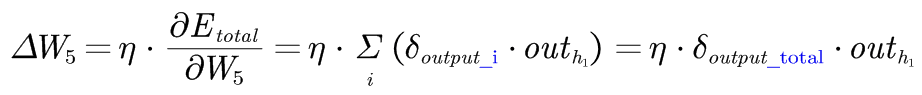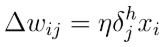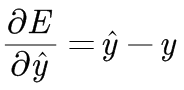绪论：背景

分类：Logistic回归

  • one-hot Encoding
    深度学习 | 神经网络理论 - 图2

核心：梯度下降

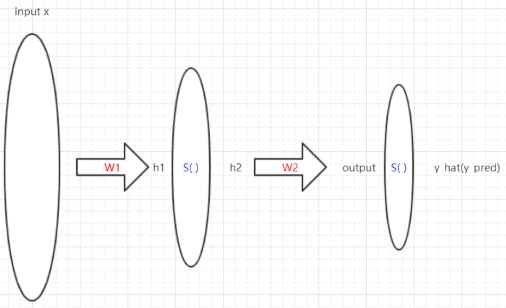
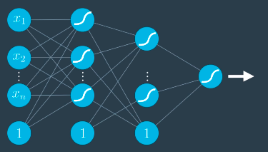
一、基本网络架构

  • 输入层x-隐藏层h-输出层y：(i, j, k)
  • 分层layer
  • 节点node

激活函数

  • sigmoid()深度学习 | 神经网络理论 - 图3

误差函数E(W,b)

  • 交叉熵
    本质：概率和误差函数之间有一定的联系
    MLP：事件发生的概率(可能性)越大，则交叉熵越小(熵越低，表示更加有序、确定)
    优化：相乘改为相加，取对数log
  • MSE：平均平方误差
    注意 权重更新的±号：对y_hat偏导后的负数(MSE对y_hat求偏导后的结果是y_hat - y：即当误差是y_hat - y时，权重更新为负号)
  • MAE：平均绝对误差
  • 误差error
    误差函数E对层输出侧(右侧)的偏导
  • 误差项delta
    误差函数E对层输入侧(左侧)的偏导
  • 权重更新
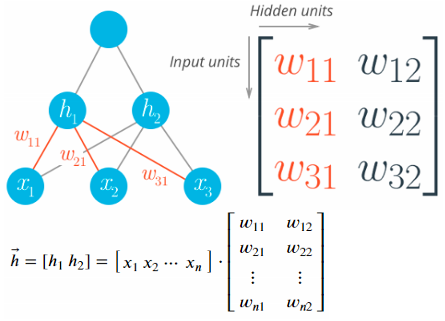
    如图output对h2的偏导==权重W2——>那么对权重W2的偏导，就是h2
    所以权重更新需要乘以“输入(h2)”
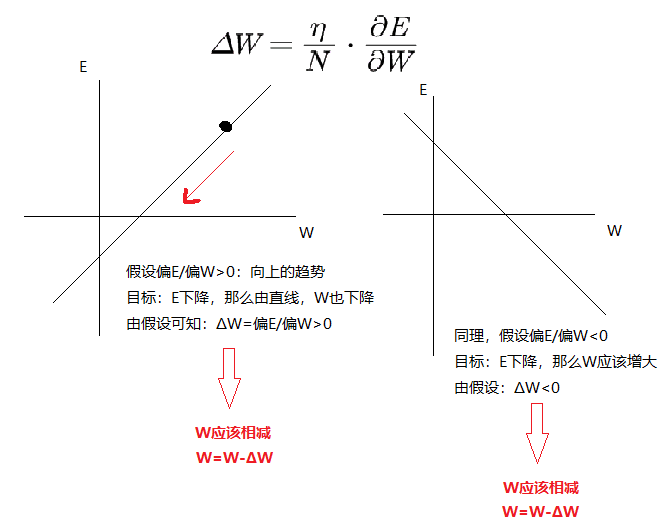
    注意：编程时，权重更新相减(前提是最初的error计算公式为y_hat - y) @梯度方向表示增加

    深度学习 | 神经网络理论 - 图4

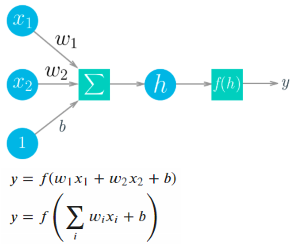
二、感知器perceptron(神经元结构)

感知器算法本质上就是梯度下降
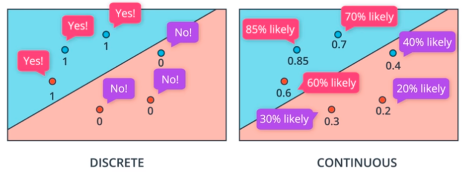
离散分类的阶跃函数==连续型感知器的sigmoid函数；多类别用softmax函数表示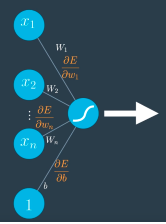
深度学习 | 神经网络理论 - 图5

  • 微分：离散值连续化
    选择距离对应的概率：距离越远正确分类的概率越大，错误分类的概率越小
    距离：样本点到当前分类界限的距离
    深度学习 | 神经网络理论 - 图6

多层感知器

  • 前向反馈Forward Feedback
  • 反向传播Backpropagation
    深度学习 | 神经网络理论 - 图7

三、神经网络架构(非线性分类器)

单层神经网络

深度学习 | 神经网络理论 - 图8

多层神经网络 深度学习 | 神经网络理论 - 图9

四、反向传播：得到误差项，更新权值

  1. 原理
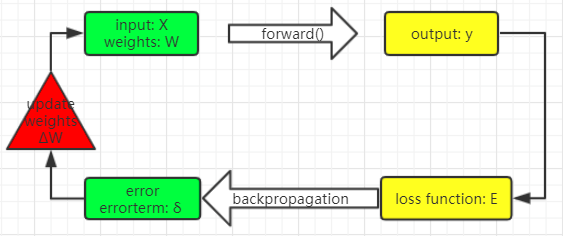
    深度学习 | 神经网络理论 - 图10
  2. 具体计算过程 参考来源
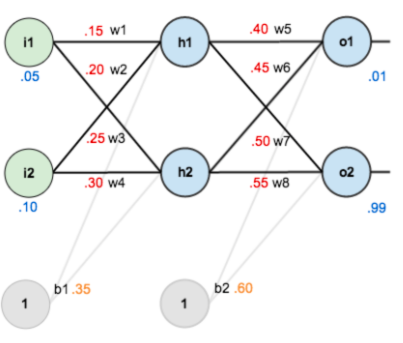
  1. 网络架构
    深度学习 | 神经网络理论 - 图11
  2. 前向传播forward
  • out_h1 = 0.5932
  • out_h2 = 0.5968
  • out_o1 = 0.7513
  • out_o2 = 0.7729
  1. 反向传播backpropagation
    (1) 计算总的误差(误差函数E)深度学习 | 神经网络理论 - 图12
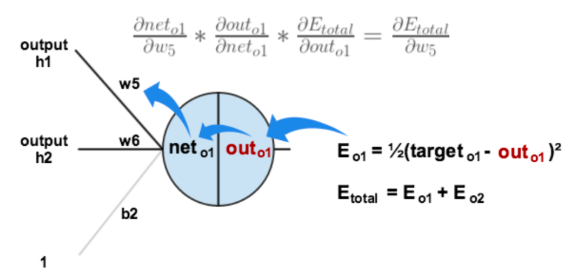
    (2) hidden层到output层，以W5为例深度学习 | 神经网络理论 - 图13
  • 误差error(每一层输出侧的误差)深度学习 | 神经网络理论 - 图14
    深度学习 | 神经网络理论 - 图15
  • 激活函数的导数深度学习 | 神经网络理论 - 图16
  • 误差项δerrorterm = error*激活函数的导数
    不妨理解为传播路径输出侧(右侧：激活函数只前)的误差
  • 权重变化ΔW：误差项δ**传播路径的输入深度学习 | 神经网络理论 - 图17
    深度学习 | 神经网络理论 - 图18
    深度学习 | 神经网络理论 - 图19Vin是该层的输入，比如经过隐藏层激活函数后的输出值
  • 权重更新W：±号的选择
    基于MSE的误差函数深度学习 | 神经网络理论 - 图20
    深度学习 | 神经网络理论 - 图21

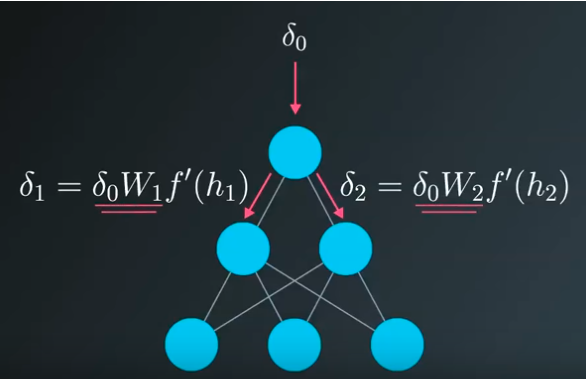
补充：误差项δ 深度学习 | 神经网络理论 - 图22 深度学习 | 神经网络理论 - 图23 f’(hj)表示隐藏层节点j 输出项的导数

五、拓展补充

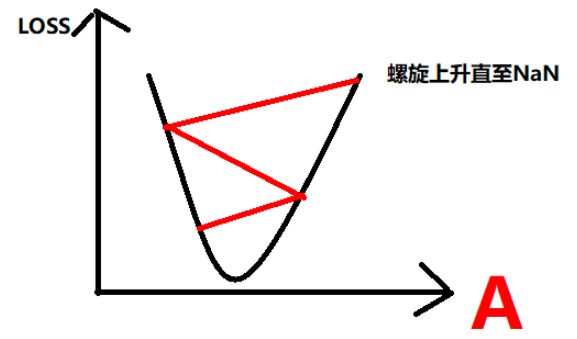
  1. 学习率太高
  • 样本数量
    学习率α 乘上1/N，N是训练集中数据量：不被训练集样本的个数影响

参考
以下两个条件成立时，网络会无法收敛，且参数迅速扩大直至变成NaN：
1)input/label值过大：如0~100
2)学习率较大，如0.1

当学习率太高/输入数据太大，会导致导数非常大，直接跳到二次函数对称轴另一边

深度学习 | 神经网络理论 - 图24

References

原理详解|含数值计算
问题 | 学习率太大