11. 盛最多水的容器

题目

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水（面积最大）。

• 链接：https://leetcode-cn.com/problems/container-with-most-water
• 说明：你不能倾斜容器，且 n 的值至少为 2。

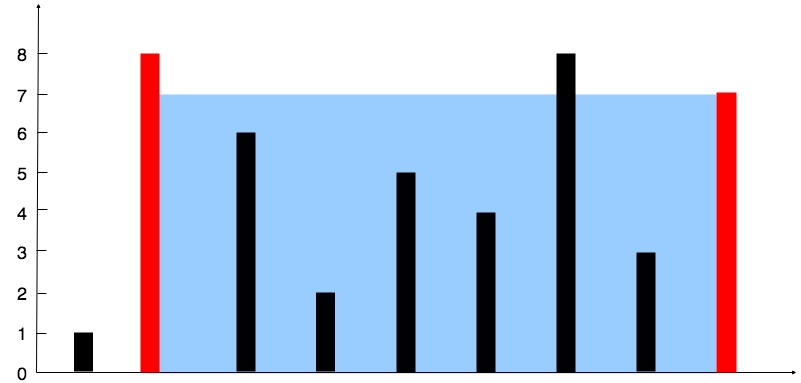
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

• 示例：

  输入：[1,8,6,2,5,4,8,3,7]
  输出：49

思路

1. 枚举：左柱子x和右柱子y，（x-y）* height_diff -> O(N^2)

   public int maxArea(int[] height) {
    int max = 0;
    for(int i = 0; i < height.length - 1; ++i){
        for(int j = i + 1; j < height.length;++j){
            //int area = _getArea(i, j);
            int area = (j - i) * Math.min(height[i], height[j]);
            max = Math.max(max, area);
        }
    }
    return max;
   }
   

2. 左右边界 i 和 j，向中间收敛：左右夹逼

设置两个指针 i 和 j，i指向最左边元素，j 指向最右边元素。这时候，宽度是最宽的，然后慢慢往中间收缩，如果中间的柱子还没左右两边的高，直接跳过，直到找到相对较高的柱子求面积，如果比初始值要大，i 和 j指向新的位置。i和j中间相遇就得到结果。

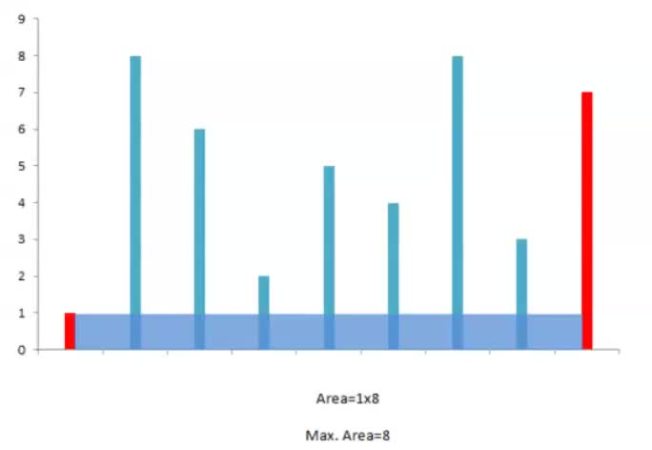
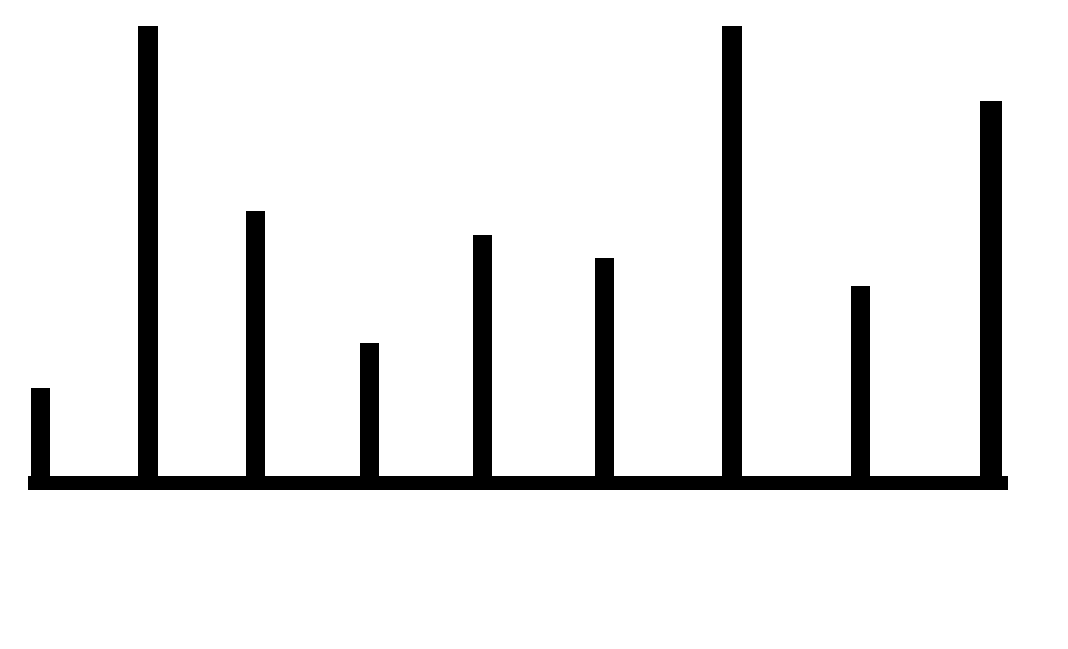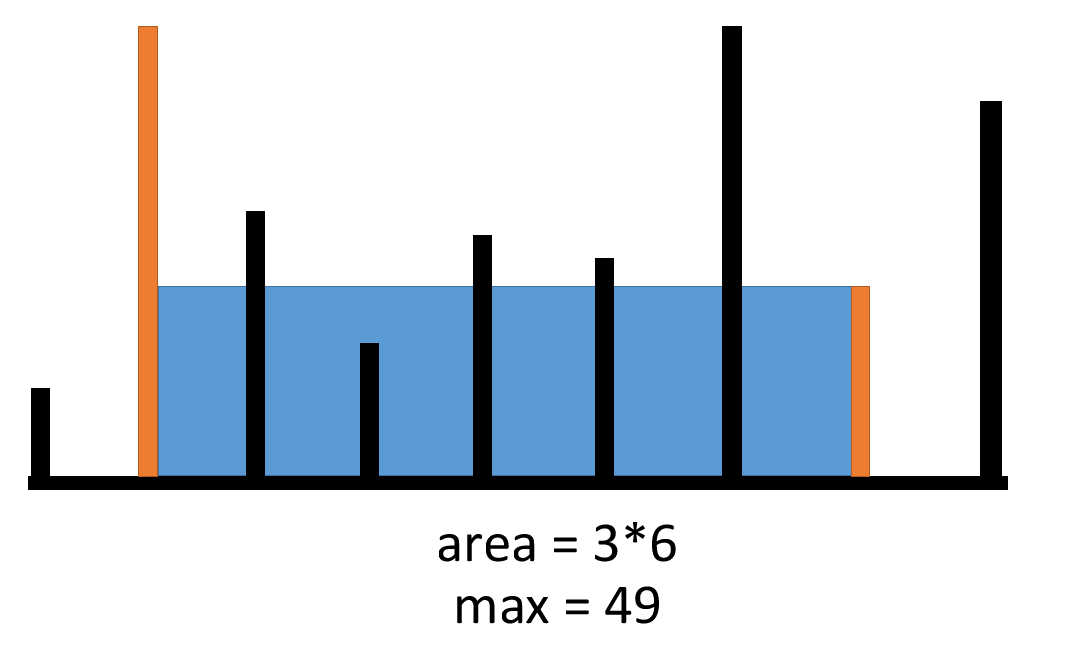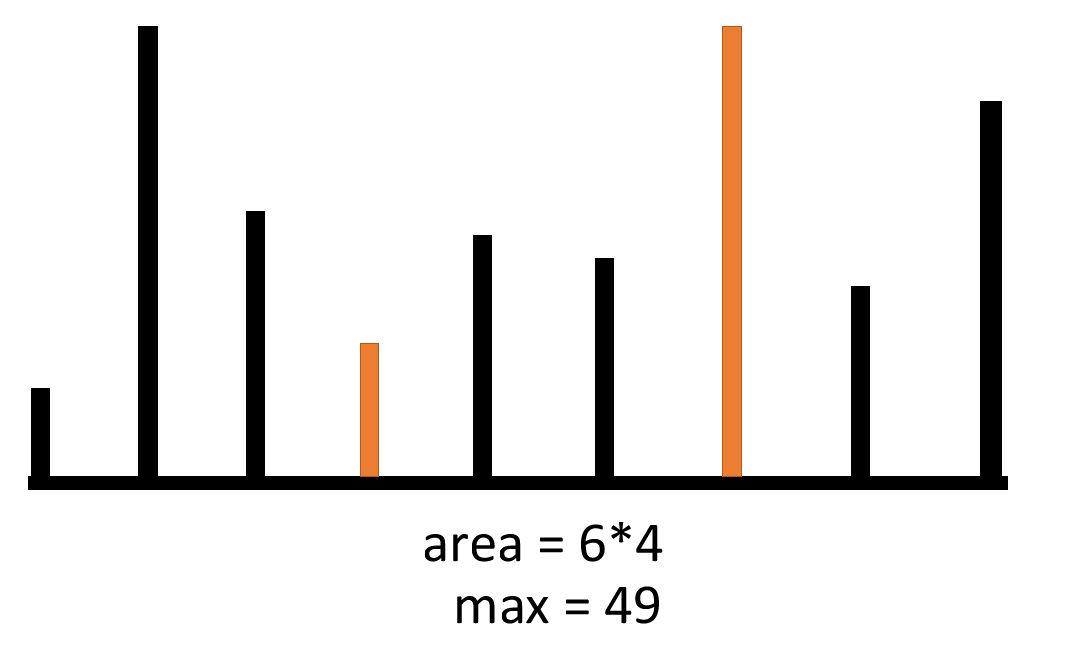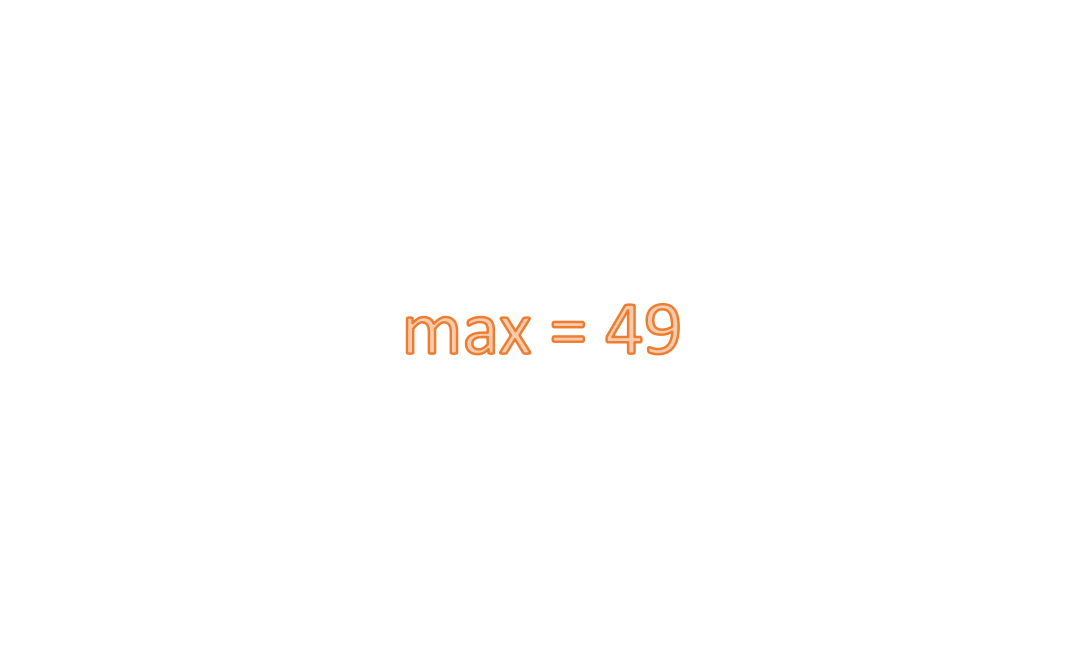
代码

// JAVA
public int maxArea(int[] height) {
    int max = 0;
    for (int i = 0, j = height.length - 1; i < j;) {
        int minHeight = height[i] < height[j] ? height[i++] : height[j--]; // 谁小谁挪
        int area = (j-i+1)*minHeight
        max = Math.max(max, area);
    }
    return max;
}

# Python
def maxArea(self, height: List[int]) -> int:
    Area = 0
    i = 0
    j = len(height) - 1
    while i < j:
        if height[i] < height[j]:
            minHeight = height[i]
            i += 1
            area = (j-i+1) * minHeight
            Area = max(Area, area)

        else:
            minHeight = height[j]
            j -= 1
            area = (j-i+1) * minHeight
            Area = max(Area, area)
     return Area

// C++
int maxArea(vector<int>& height) {
    int i = 0;
    int j = height.size() - 1;
    int res = 0;
    while (i < j) {
        if (height[i] < height[j]) {
            int minHeight = height[i];
            int area = minHeight * (j-i);
            res = max(area, res);
            i++;
        }else{
            int minHeight = height[j];
            int area = minHeight * (j-i);
            res = max(area, res);
            j--;
        }
    }
    return res; 
}