一.算法简介
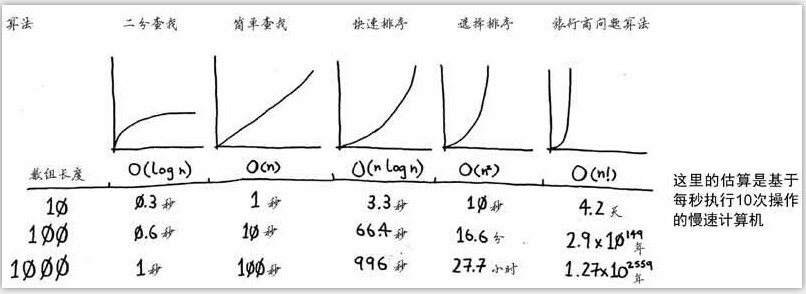
“O” 表示算法 分析速度()
简单查找 从第一个数据开始查找
二分查找 前提:有序数据 二分查找从中间数据开始查找,每次都会排除一半的数据
O 操作数
简单查找 n步
二分查找 log2 N
LOG2(8)=3相当于,2的3次方等于8
O 运行时间
O(log n) 对数时间
O(n) 线性时间,常量时间
O(n * log N)快速排序
O(n!) 最慢排序
二 选择排序
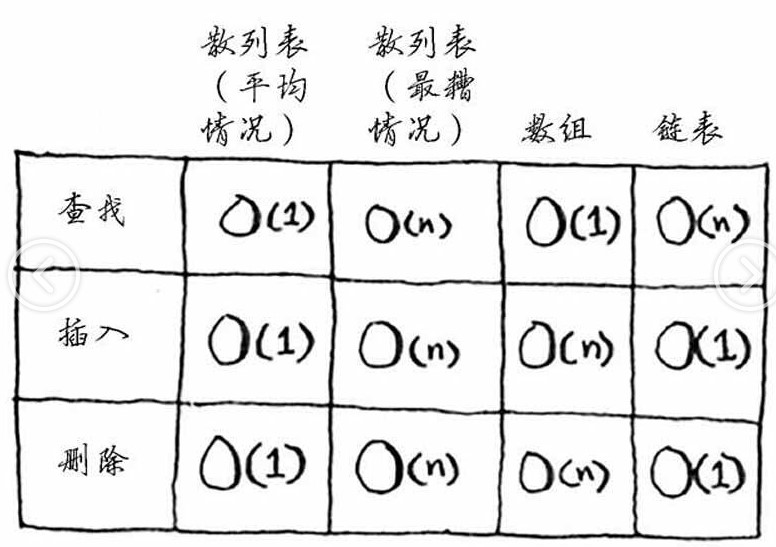
数组—链表
数组 先申请,在存储 顺序存储
链表 随机存储,随机插入
操作时间 O(n) 线性时间 O(1) 常量时间
| 数组 | 链表 | |
|---|---|---|
| 读取 | O(1) | O(n) |
| 插入 | O(n) |
O(1) |
| 删除 | O(n) |
O(1) |
选择排序:选择最大或最下数,存放在序列的起始位置,在从剩下的数据中继续选择。存放
三 递归
1.描述
解决类似循环的查找问题的方法,分别是do while 和递归
while 性能更好
递归 更容易理解
2.递归:包含 基线条件、递归条件
基线条件:防止递归死循环
递归条件: 调用自己
3.栈 :先进后出
递归操作会使用调用栈分配内存
四 快速排序
1.描述
快速排序——一种常用的优雅的排序算法。快速排序使用分而治之的策略。
2.分而治之(D&C)
例子:何将一块地均匀地分成方块,并确保分出的方块是最大,找出最大地的方块,然后剩下剩余不足的小块,
继续通过宽高倍数分割,直到满足基线条件为止。
原理:
a.找出简单的基线条件
b.确定如何缩小问题的规模,使其符合基线条件
3.快速排序
快速排序速度比选择排序速度快—基准值选择
4.大O表示法:
平均情况和最糟情况:
在最糟情况下,栈长为O(n),而在最佳情况下,栈长为O(logn)。取决于基准值
五 散列表(Hash表)
1.描述
散列表:key—value的一种方式
散列函数总是将同样的输入映射到相同的索引。
散列函数将不同的输入映射到不同的索引。
散列函数知道数组有多大,只返回有效的索引。