AC：4/4

前三题很顺，第四题还是图论题，百度了才知道自己原来的算法是个憨憨，还好用了1个小时10分钟AK了。

第一题：5479. 千位分隔数

  • 题目难度Easy

给你一个整数 n，请你每隔三位添加点（即 “.” 符号）作为千位分隔符，并将结果以字符串格式返回。

示例 1：
输入：n = 987
输出：“987”

示例 2：
输入：n = 1234
输出：“1.234”

示例 3：
输入：n = 123456789
输出：“123.456.789”

示例 4：
输入：n = 0
输出：“0”

提示：

  • 0 <= n < 2^31

    答案：

    1. class Solution:
    2.   def thousandSeparator(self, n: int) -> str:
    3.       n=str(n)
    4.       k=len(n)
    5.       ans=""
    6.       for i in range(k):
    7.           if (k-i)%3==0 and i!=0:
    8.               ans+="."
    9.           ans+=n[i]
    10.       return ans

    思路：

    python字符串无敌

    第二题：5480. 可以到达所有点的最少点数目

    给你一个 有向无环图 ， n 个节点编号为 0 到 n-1 ，以及一个边数组 edges ，其中 edges[i] = [from, to] 表示一条从点 from 到点 to 的有向边。

    找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。
    你可以以任意顺序返回这些节点编号。

    示例 1：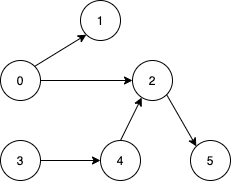
    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图2
    输入：n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
    输出：[0,3]
    解释：从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。
    示例 2：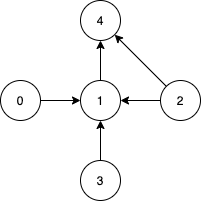
    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图3
    输入：n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
    输出：[0,2,3]
    解释：注意到节点 0，3 和 2 无法从其他节点到达，所以我们必须将它们包含在结果点集中，这些点都能到达节点 1 和 4 。


    提示：

  • 2 <= n <= 10^5

  • 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
  • edges[i].length == 2
  • 0 <= from to < n

  • 所有点对 (from, to) 互不相同。

    答案：

    1. class Solution:
    2.   def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
    3.       rudu = {}
    4.       for i in range(n):
    5.           rudu[i]=0
    6.       for i,j in edges:
    7.           rudu[j]+=1
    8.       ans=[]
    10.       for i,count in rudu.items():
    11.           if count==0:
    12.               ans.append(i)
    13.       return ans

    思路：

    分析了一下，找入度为0的点就行了。

    第三题：5481. 得到目标数组的最少函数调用次数

    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图4

    题目：

    给你一个与 nums 大小相同且初始值全为 0 的数组 arr ，请你调用以上函数得到整数数组 nums 。
    请你返回将 arr 变成 nums 的最少函数调用次数。
    答案保证在 32 位有符号整数以内。

    示例 1：
    输入：nums = [1,5]
    输出：5
    解释：给第二个数加 1 ：[0, 0] 变成 [0, 1] （1 次操作）。
    将所有数字乘以 2 ：[0, 1] -> [0, 2] -> [0, 4] （2 次操作）。
    给两个数字都加 1 ：[0, 4] -> [1, 4] -> [1, 5] （2 次操作）。
    总操作次数为：1 + 2 + 2 = 5 。

示例 2：
输入：nums = [2,2]
输出：3
解释：给两个数字都加 1 ：[0, 0] -> [0, 1] -> [1, 1] （2 次操作）。
将所有数字乘以 2 ： [1, 1] -> [2, 2] （1 次操作）。
总操作次数为： 2 + 1 = 3 。

示例 3：
输入：nums = [4,2,5]
输出：6
解释：（初始）[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5] （nums 数组）。

示例 4：
输入：nums = [3,2,2,4]
输出：7

示例 5：
输入：nums = [2,4,8,16]
输出：8


提示：

  • 1 <= nums.length <= 10^5

  • 0 <= nums[i] <= 10^9

    答案：

    1. class Solution:
    2.   def minOperations(self, nums: List[int]) -> int:
    4.       ans=0
    5.       @functools.lru_cache(None)
    6.       def count(num):
    7.           res=0
    8.           minus=0
    9.           while num:
    10.               if num%2==1:
    11.                   res+=1
    12.                   minus+=1
    13.                   num=num//2
    14.               else:
    15.                   res+=1
    16.                   num=num//2
    17.           return res,minus
    19.       temp=0
    20.       for num in nums:
    21.           res,minus = count(num)
    22.           ans+=minus
    23.           temp=max(temp,res)
    24.       ans+=temp
    25.       return ans-1

    思路：

    总的来说，都是偶数才除2，不然就得减到偶数。
    统计的时候，除二是一起操作的，统计最大值，减一是分开操作的，累加即可。
    最后为什么多了1，我也没分析，实践出真知，估计除二多算了一次把。

    第四题：5482. 二维网格图中探测环

    题目：

    给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。
    一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。
    同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。
    如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

    示例 1：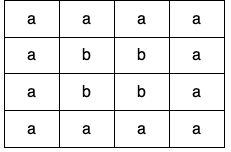
    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图5
    输入：grid = [[“a”,”a”,”a”,”a”],[“a”,”b”,”b”,”a”],[“a”,”b”,”b”,”a”],[“a”,”a”,”a”,”a”]]输出：true解释：如下图所示，有 2 个用不同颜色标出来的环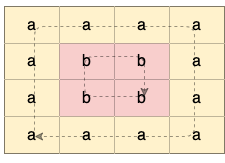：20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图6
    示例 2：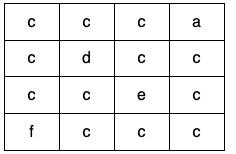
    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图7
    输入：grid = [[“c”,”c”,”c”,”a”],[“c”,”d”,”c”,”c”],[“c”,”c”,”e”,”c”],[“f”,”c”,”c”,”c”]]输出：true解释：如下图所示，只有高亮所示的一个合法环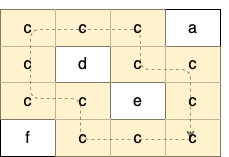：20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图8
    示例 3：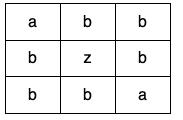
    20200822 第33周双周赛 score：4/4 排名：396 / 3304 - 图9
    输入：grid = [[“a”,”b”,”b”],[“b”,”z”,”b”],[“b”,”b”,”a”]]
    输出：false


    提示：

  • m == grid.length

  • n == grid[i].length
  • 1 <= m <= 500
  • 1 <= n <= 500

  • grid 只包含小写英文字母。

    答案：

    ```python from collections import deque,defaultdict class Solution: def containsCycle(self, grid: List[List[str]]) -> bool:

    1.   if not grid or not grid[0]:return False
    2.   m,n=len(grid),len(grid[0])
    3.   directs=[(-1,0),(1,0),(0,1),(0,-1)]
    5.   record=[1]*(m*n)
    7.   rudu=defaultdict(int)
    8.   de=[]
    9.   for i in range(m):
    10.       for j in range(n):
    11.           word=grid[i][j]
    12.           for ix,iy in directs:
    13.               new_x,new_y=i+ix,j+iy
    14.               if new_x<0 or new_x>=m or new_y<0 or new_y>=n:continue 
    15.               if grid[new_x][new_y]==word:
    16.                   rudu[(i,j)]+=1
    17.           if rudu[(i,j)]<2:
    18.               de.append((i,j))
    19.               record[i*n+j]=0
    while de:
        new_q=[]
        for i,j in de:
            word=grid[i][j]
            for ix,iy in directs:
                new_x,new_y=i+ix,j+iy
                if new_x<0 or new_x>=m or new_y<0 or new_y>=n:continue 
                if record[new_x*n+new_y]==1 and grid[new_x][new_y]==word:
                    rudu[(new_x,new_y)]-=1
                    if rudu[(new_x,new_y)]<2:
                        record[new_x*n+new_y]=0
                        new_q.append((new_x,new_y))
        de=new_q
    for i in range(m):
        for j in range(n):
            if record[i*n+j]>0:
                return True
    return False

```

思路：

无向图找环，入度为2达标，一旦入度小于2，删掉边更新入度，循环。
删到最后还有边就有环，不然就无环。