813. 最大平均值和的分组

题目：

我们将给定的数组 A 分成 K 个相邻的非空子数组 ，我们的分数由每个子数组内的平均值的总和构成。计算我们所能得到的最大分数是多少。
注意我们必须使用 A 数组中的每一个数进行分组，并且分数不一定需要是整数。
示例:
输入: 
A = [9,1,2,3,9]
K = 3
输出: 20
解释: 
A 的最优分组是[9], [1, 2, 3], [9]. 得到的分数是 9 + (1 + 2 + 3) / 3 + 9 = 20.
我们也可以把 A 分成[9, 1], [2], [3, 9].
这样的分组得到的分数为 5 + 2 + 6 = 13, 但不是最大值.
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-sum-of-averages
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

答案：

时间：

15min

class Solution:
    def largestSumOfAverages(self, A: List[int], K: int) -> float:
        n=len(A)
        dp=[[0]*(K) for _ in range(n)]
        prefix=[0]
        for num in A:
            prefix.append(prefix[-1]+num)
        for i in range(n):
            for j in range(K):
                if j==0:
                    dp[i][j] = (prefix[i+1]-prefix[0]) / (i + 1)
                elif i<j:break
                else:
                    for k in range(i):
                        dp[i][j]=max(dp[i][j],dp[k][j-1]+(prefix[i+1]-prefix[k+1])/(i-k))
        return dp[-1][-1]

要点：

1. dp 定义:

前i个分j 段的 target值，注意初始化条件

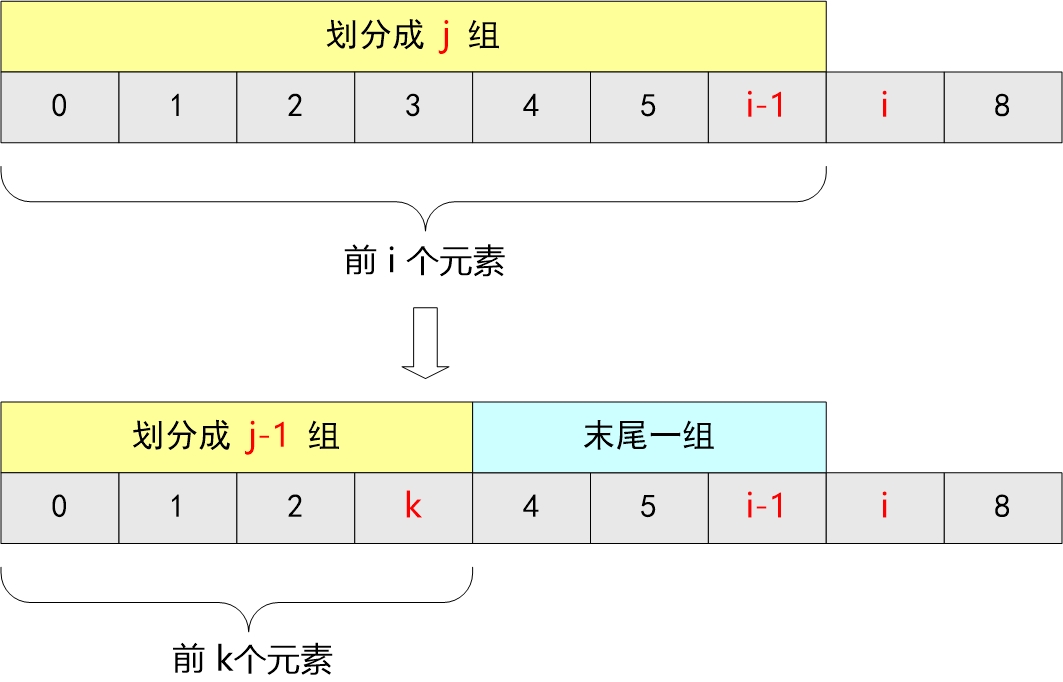
2. 转移：

还是这张图，看着转移就可以了

其他：

代码报错：无