410. 分割数组的最大值

题目：

给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
注意:
数组长度 n 满足以下条件:
1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)
示例:
输入:
nums = [7,2,5,10,8]
m = 2
输出:
18
解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/split-array-largest-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

答案：

时间：

45min，未果吐血。

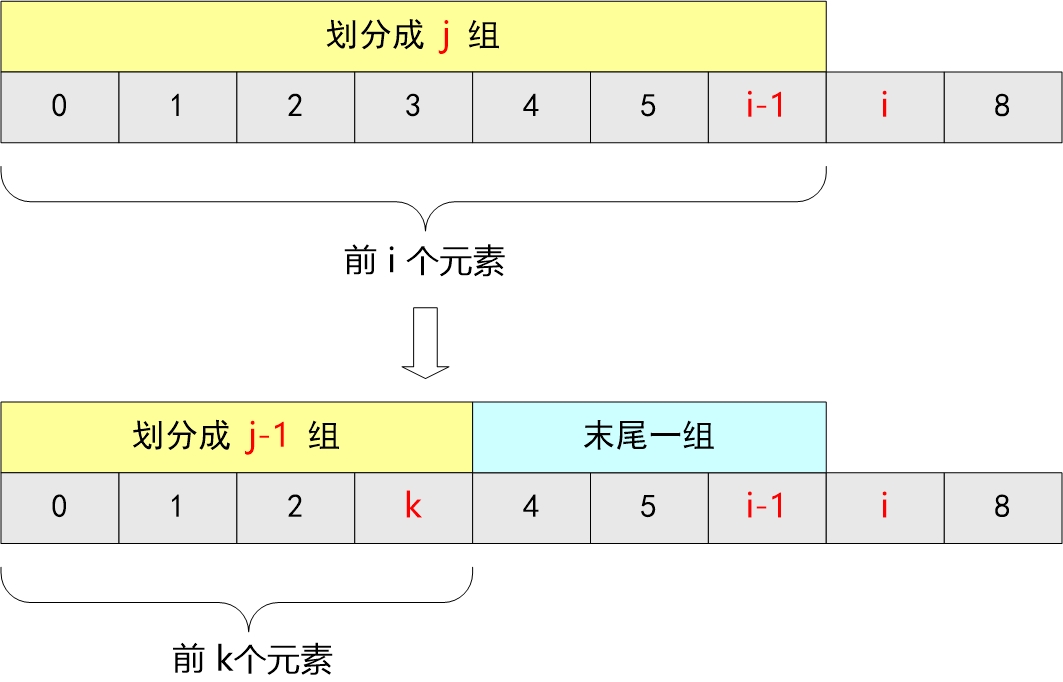
class Solution:
    def splitArray(self, nums: List[int], m: int) -> int:
        n=len(nums)
        dp=[[float("inf")]*(m+1) for _ in range(n+1)]
        sub=[0]
        for num in nums:
            sub.append(sub[-1]+num)
        dp[0][0]=0
        for i in range(1,n+1):
            for j in range(1,min(i,m)+1):
                for k in range(i):
                    dp[i][j]=min(dp[i][j],max(dp[k][j-1], sub[i]-sub[k]) )
        return dp[-1][-1]

要点：

1. dp 定义

dp[i][j]: 前i 个被切j 段的所要target

2. 转移

遍历前i个，找第j段，max是由target的定义给出。

dp[i][j]←max(dp[k][j-1],prefix(i)-prefix(k))

3. 菜啊

其他：

代码报错：无