一、传统统计学预测

时间序列分析法

1、指数平滑法

yt-1%0A%5C%5Cy_t%E6%98%AF%E6%97%B6%E9%97%B4t%E7%9A%84%E6%97%B6%E9%97%B4%E5%80%BC%0A%5C%5Ca%E6%98%AF%E5%B9%B3%E6%BB%91%E6%8C%87%E6%95%B0%EF%BC%8C%E5%8F%96%E5%80%BC%E8%8C%83%E5%9B%B4%E3%80%900%2C1%E3%80%91%0A#card=math&code=y%7Bt%2B1%7D%3Da%20%2Ay_t%2B%281-a%29y_t-1%0A%5C%5Cy_t%E6%98%AF%E6%97%B6%E9%97%B4t%E7%9A%84%E6%97%B6%E9%97%B4%E5%80%BC%0A%5C%5Ca%E6%98%AF%E5%B9%B3%E6%BB%91%E6%8C%87%E6%95%B0%EF%BC%8C%E5%8F%96%E5%80%BC%E8%8C%83%E5%9B%B4%E3%80%900%2C1%E3%80%91%0A)

优点：简单、适合趋势预测、模糊预测

缺点：准确率不高、需要趋势性较好的数据

2、自回归移动模型 ARIMA

将非平稳的时间序列转化为平稳时间序列

将结果变量做自回归（AR）和自平移（MA）

二、机器学习预测算法

1、灰色预测

概念

1. 灰色预测是一种对含有不确定因素（如服装预测的节假日销量暴涨）的系统进行预测的方法。
2. 用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。

分类

1. 灰色时间序列预测：即用观察到的反映预测对象特征的时间序列来构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。
2. 畸变预测：即通过灰色模型预测异常值出现的时刻，预测异常值什么时候出现在特定时区内。
3. 系统预测：通过对系统行为特征指标建立一组相互关联的灰色预测模型，预测系统中众多变量间的相互协调关系的变化
4. 拓扑预测：将原始数据作曲线，在曲线上按定值寻找该定值发生的所有时点，并以该定值为框架构成时点数列，然后建立模型预测该定值所发生的时点。

适用性

• 灰色预测模型可针对数量非常少（比如仅4个），数据完整性和可靠性较低的数据序列进行有效预测，其利用微分方程来充分挖掘数据的本质，建模所需信息少，精度较高，运算简便，易于检验，也不用考虑分布规律或变化趋势等。
• 灰色预测模型一般只适用于短期预测，只适合指数增长的预测，比如人口数量，航班数量，用水量预测，工业产值预测等

步骤

1. 建模机理
2. 把原始数据加工成生成数列；
   • 累加生成
   • 累减生成
   • 映射生成
3. 对残差（模型计算值与实际值之差）修订后，建立差分微分方程模型；
4. 基于关联度收敛的分析；
5. GM模型所得数据须经过逆生成还原后才能用。
6. 采用“五步建模（系统定性分析、因素分析、初步量化、动态量化、优化）”法，建立一种差分微分方程模型GM(1,1）预测模型。

GM（1，1）模型

%7D%26%3D%20%5Clbrace%20x%5E%7B(0)%7D(1)%2Cx%5E%7B(0)%7D(2)%EF%BC%8C%5Ccdots%EF%BC%8Cx%5E%7B(0)%7D(n)%20%5Crbrace%20%5C%5C%5C%5C%0Ax%5E%7B(1)%7D%26%3D%20%5Clbrace%20x%5E%7B(1)%7D(1)%2Cx%5E%7B(1)%7D(2)%EF%BC%8C%5Ccdots%EF%BC%8Cx%5E%7B(1)%7D(n)%20%5Crbrace%20%5C%5C%5C%5C%0Ax%5E%7B(1)%7D(k)%26%3D%5Csum%20%7Bt%3D1%7D%5Ek%20x%5E%7B(0)%7D(i)%20%5Cquad%20%20k%3D1%2C2%2C%5Ccdots%2Cn%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Ax%5E%7B%280%29%7D%26%3D%20%5Clbrace%20x%5E%7B%280%29%7D%281%29%2Cx%5E%7B%280%29%7D%282%29%EF%BC%8C%5Ccdots%EF%BC%8Cx%5E%7B%280%29%7D%28n%29%20%5Crbrace%20%5C%5C%5C%5C%0Ax%5E%7B%281%29%7D%26%3D%20%5Clbrace%20x%5E%7B%281%29%7D%281%29%2Cx%5E%7B%281%29%7D%282%29%EF%BC%8C%5Ccdots%EF%BC%8Cx%5E%7B%281%29%7D%28n%29%20%5Crbrace%20%5C%5C%5C%5C%0Ax%5E%7B%281%29%7D%28k%29%26%3D%5Csum%20%7Bt%3D1%7D%5Ek%20x%5E%7B%280%29%7D%28i%29%20%5Cquad%20%20k%3D1%2C2%2C%5Ccdots%2Cn%0A%5Cend%7Baligned%7D%0A)

设%7D#card=math&code=x%5E%7B%280%29%7D)满足一阶常微分方程(白化方程)，即GM（1,1）

%7D%5Cover%7B%5Crm%20d%7Dt%7D%2Bax%5E%7B(1)%7D%3Du%20%5Ctag%7B3%7D%5C%5C%0A#card=math&code=%7B%7B%5Crm%20d%7Dx%5E%7B%281%29%7D%5Cover%7B%5Crm%20d%7Dt%7D%2Bax%5E%7B%281%29%7D%3Du%20%5Ctag%7B3%7D%5C%5C%0A)

此方程满足初始条件，当时，%7D%3Dx%5E%7B(1)%7D(t_0)#card=math&code=x%5E%7B%281%29%7D%3Dx%5E%7B%281%29%7D%28t_0%29)的解为

%7D(t)%3D%5Cleft%5Bx%5E%7B(1)%7D(t_0)-%5Cfrac%20ua%5Cright%5D%20e%5E%7B-a(t-t_0)%7D%2B%5Cfrac%20ua%0A#card=math&code=x%5E%7B%281%29%7D%28t%29%3D%5Cleft%5Bx%5E%7B%281%29%7D%28t_0%29-%5Cfrac%20ua%5Cright%5D%20e%5E%7B-a%28t-t_0%29%7D%2B%5Cfrac%20ua%0A)

对等间隔取样的离散值（注意到）则为

%7D(k%2B1)%3D%5Cleft%5Bx%5E%7B(1)%7D(1)-%5Cfrac%20ua%5Cright%5D%20e%5E%7B-ak%7D%2B%5Cfrac%20ua%0A#card=math&code=x%5E%7B%281%29%7D%28k%2B1%29%3D%5Cleft%5Bx%5E%7B%281%29%7D%281%29-%5Cfrac%20ua%5Cright%5D%20e%5E%7B-ak%7D%2B%5Cfrac%20ua%0A)

其中：α称为发展灰数；μ称为内生控制灰数

将$k=2,3\cdots,n %E5%BC%8F%E4%B8%AD%E3%80%82%E7%94%A8%E5%B7%AE%E5%88%86%E4%BB%A3%E6%9B%BF%E5%BE%AE%E5%88%86%EF%BC%8C%E5%8F%88%E5%9B%A0%E7%AD%89%E9%97%B4%E9%9A%94%E5%8F%96%E6%A0%B7%EF%BC%8C#card=math&code=%E4%BB%A3%E5%85%A5%283%29%E5%BC%8F%E4%B8%AD%E3%80%82%E7%94%A8%E5%B7%AE%E5%88%86%E4%BB%A3%E6%9B%BF%E5%BE%AE%E5%88%86%EF%BC%8C%E5%8F%88%E5%9B%A0%E7%AD%89%E9%97%B4%E9%9A%94%E5%8F%96%E6%A0%B7%EF%BC%8C)\Delta t=(t+1)-t=1$故得：

%7D(2)%7D%7B%5CDelta%20t%7D%26%3D%7B%5CDelta%20x%5E%7B(1)%7D(2)%7D%5C%5C%0A%26%3Dx%5E%7B(1)%7D(2)-x%5E%7B(1)%7D(1)%3Dx%5E%7B(0)%7D(2)%5C%5C%0A%5Cfrac%7B%5CDelta%20x%5E%7B(1)%7D(3)%7D%7B%5CDelta%20t%7D%26%3Dx%5E%7B(0)%7D(3)%5C%5C%0A%5Cfrac%7B%5CDelta%20x%5E%7B(1)%7D(n)%7D%7B%5CDelta%20t%7D%26%3Dx%5E%7B(0)%7D(n)%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cfrac%7B%5CDelta%20x%5E%7B%281%29%7D%282%29%7D%7B%5CDelta%20t%7D%26%3D%7B%5CDelta%20x%5E%7B%281%29%7D%282%29%7D%5C%5C%0A%26%3Dx%5E%7B%281%29%7D%282%29-x%5E%7B%281%29%7D%281%29%3Dx%5E%7B%280%29%7D%282%29%5C%5C%0A%5Cfrac%7B%5CDelta%20x%5E%7B%281%29%7D%283%29%7D%7B%5CDelta%20t%7D%26%3Dx%5E%7B%280%29%7D%283%29%5C%5C%0A%5Cfrac%7B%5CDelta%20x%5E%7B%281%29%7D%28n%29%7D%7B%5CDelta%20t%7D%26%3Dx%5E%7B%280%29%7D%28n%29%5C%5C%0A%5Cend%7Baligned%7D%0A)

%7D(2)%2Bax%5E%7B(1)%7D(2)%3Du%20%5C%5C%0Ax%5E%7B(0)%7D(3)%2Bax%5E%7B(1)%7D(3)%3Du%20%5C%5C%0A%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5C%5C%0Ax%5E%7B(0)%7D(n)%2Bax%5E%7B(1)%7D(n)%3Du%20%5C%5C%0A%5Cend%7Bcases%7D%0A#card=math&code=%5Cbegin%7Bcases%7D%0Ax%5E%7B%280%29%7D%282%29%2Bax%5E%7B%281%29%7D%282%29%3Du%20%5C%5C%0Ax%5E%7B%280%29%7D%283%29%2Bax%5E%7B%281%29%7D%283%29%3Du%20%5C%5C%0A%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5Ccdots%5C%5C%0Ax%5E%7B%280%29%7D%28n%29%2Bax%5E%7B%281%29%7D%28n%29%3Du%20%5C%5C%0A%5Cend%7Bcases%7D%0A)

将式(xxxxx)矩阵化：

%7D(2)%5C%5C%0Ax%5E%7B(0)%7D(3)%5C%5C%0A%5Cvdots%20%5C%5C%0Ax%5E%7B(0)%7D(n)%5C%5C%0A%5Cend%7Bmatrix%7D%0A%5Cright%5D%0A%0A%5Cquad%0AB%3D%5Cleft%5B%0A%5Cbegin%7Bmatrix%7D%0A-x%5E%7B(1)%7D(2)%20%26%201%5C%5C%0A-x%5E%7B(1)%7D(3)%20%26%201%5C%5C%0A%5Cvdots%20%26%20%5Cvdots%20%5C%5C%0A-x%5E%7B(1)%7D(n)%20%26%201%5C%5C%0A%5Cend%7Bmatrix%7D%0A%5Cright%5D%0A#card=math&code=U%3D%5Cleft%5B%0A%5Cbegin%7Bmatrix%7D%0Aa%5C%5C%0Au%5Cend%7Bmatrix%7D%0A%5Cright%5D%0A%0A%5Cquad%0AY%3D%5Cleft%5B%0A%5Cbegin%7Bmatrix%7D%0Ax%5E%7B%280%29%7D%282%29%5C%5C%0Ax%5E%7B%280%29%7D%283%29%5C%5C%0A%5Cvdots%20%5C%5C%0Ax%5E%7B%280%29%7D%28n%29%5C%5C%0A%5Cend%7Bmatrix%7D%0A%5Cright%5D%0A%0A%5Cquad%0AB%3D%5Cleft%5B%0A%5Cbegin%7Bmatrix%7D%0A-x%5E%7B%281%29%7D%282%29%20%26%201%5C%5C%0A-x%5E%7B%281%29%7D%283%29%20%26%201%5C%5C%0A%5Cvdots%20%26%20%5Cvdots%20%5C%5C%0A-x%5E%7B%281%29%7D%28n%29%20%26%201%5C%5C%0A%5Cend%7Bmatrix%7D%0A%5Cright%5D%0A)

所以矩阵形式为，GM(1,1)模型可以表示为

方程组的最小二乘估计为

%5E%7B-1%7DB%5ETY%0A#card=math&code=%5Chat%7BU%7D%3D%5Cleft%5B%0A%5Cbegin%7Bmatrix%7D%0A%5Chat%20a%5C%5C%0A%5Chat%20u%5Cend%7Bmatrix%7D%0A%5Cright%5D%3D%28B%5ETB%29%5E%7B-1%7DB%5ETY%0A)

把估计值与代入（xxx）式得时间响应方程

%7D(k%2B1)%3D%5Cleft%5Bx%5E%7B(1)%7D(1)-%5Cfrac%7B%5Chat%20u%7D%7B%5Chat%20a%7D%5Cright%5D%20e%5E%7B-%5Chat%20ak%7D%2B%5Cfrac%7B%5Chat%20u%7D%7B%5Chat%20a%7D%0A#card=math&code=%5Chat%20x%5E%7B%281%29%7D%28k%2B1%29%3D%5Cleft%5Bx%5E%7B%281%29%7D%281%29-%5Cfrac%7B%5Chat%20u%7D%7B%5Chat%20a%7D%5Cright%5D%20e%5E%7B-%5Chat%20ak%7D%2B%5Cfrac%7B%5Chat%20u%7D%7B%5Chat%20a%7D%0A)

精度检验

1. 残差检验
   • 残差：%3Dx%5E%7B(0)%7D(k)-%5Chat%20x%5E%7B(0)%7D(k)%20%5Cquad%20k%3D1%2C2%2C%5Ccdots%2Cn%3B#card=math&code=E%28k%29%3Dx%5E%7B%280%29%7D%28k%29-%5Chat%20x%5E%7B%280%29%7D%28k%29%20%5Cquad%20k%3D1%2C2%2C%5Ccdots%2Cn%3B)
   • 相对残差：%3D%5Cfrac%20%7Bx%5E%7B(0)%7D(k)-%5Chat%20x%5E%7B(0)%7D(k)%7D%7Bx%5E%7B(0)%7D(k)%7D%20%5Cquad%20k%3D1%2C2%2C%5Ccdots%2Cn%3B#card=math&code=e%28k%29%3D%5Cfrac%20%7Bx%5E%7B%280%29%7D%28k%29-%5Chat%20x%5E%7B%280%29%7D%28k%29%7D%7Bx%5E%7B%280%29%7D%28k%29%7D%20%5Cquad%20k%3D1%2C2%2C%5Ccdots%2Cn%3B)
2. 关联度检验
3. 后验差检验

2、神经网络预测

简介请见：bp神经网络.md

2.1循环神经网络（RNN）

长短期记忆模型LSTM模型（遗忘门、输入门、输出门）

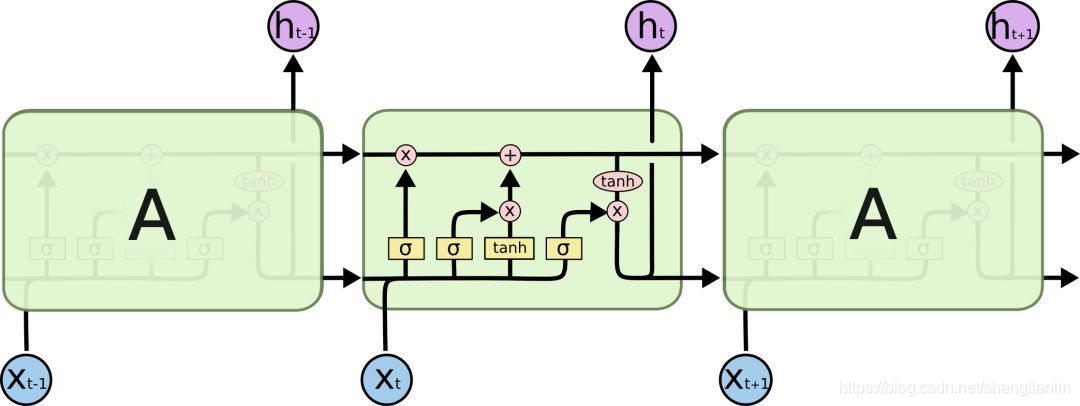
遗忘门：

用以控制对之前的记忆是否保留，保留多少

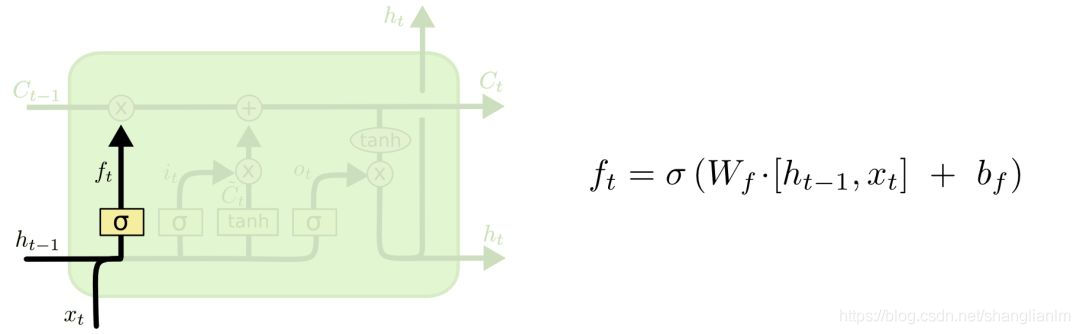
是前一输入

是当前输入 $ x_t*U_f=W_f[x_t]$

是遗忘门的值

是激活函数 ，选择Signmid，值选择0或者1 ，代表 删除/保留

输入门:

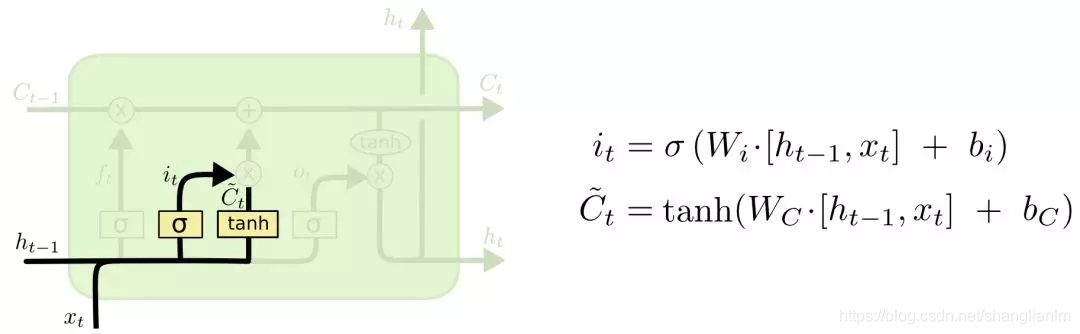
用以控制输入是否加入到记忆中，用以下一时刻的计算

输出门

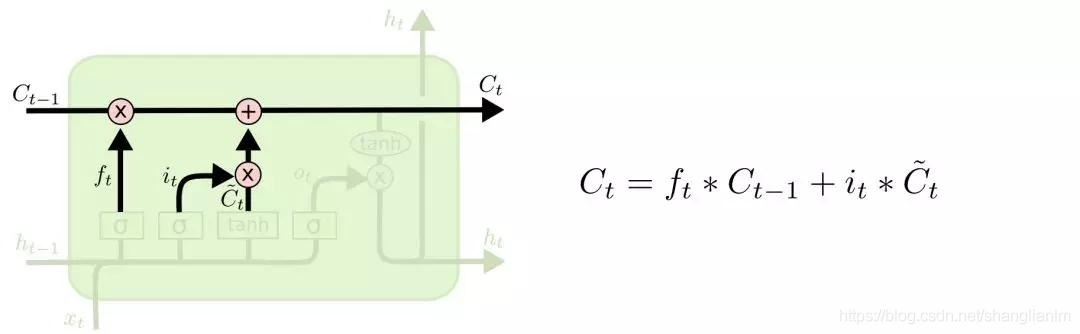
代表是否保留

代表是否加入

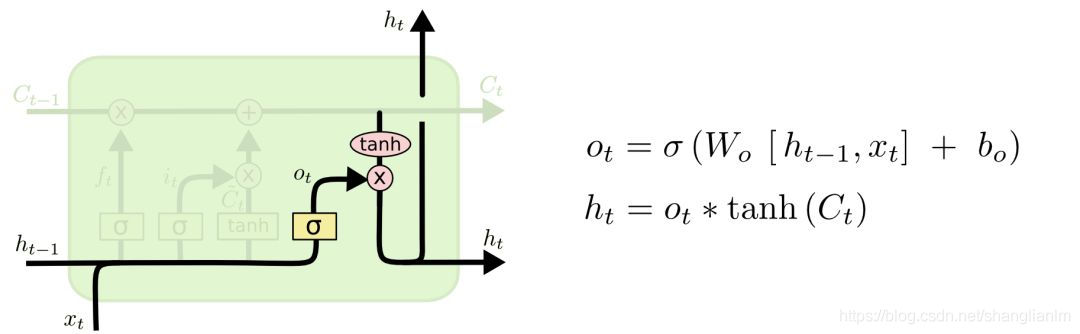
最终我们得到

3、支持向量机

3.1、简介

支持向量机(support vector machine)是一种分类算法，但是也可以做回归。（二分类模型）

• 输入标签为连续值则做回归（SVR支持向量回归）
• 输入标签为分类值则用做分类

过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

3.2、优缺点

1. 优点区
   • 可用于线性/非线性分类，也可以用于回归；
   • 低泛化误差；
   • 容易解释；
   • 计算复杂度较低；
   • 可以解决高维问题；
2. 缺点区

• 对参数和核函数的选择比较敏感；
• 原始的SVM只比较擅长处理二分类问题；

SVM属于监督学习算法，监督学习流程如图所示：

3.3、名词解释

1. 超平面方程:超平面由法向量w和位移项b决定。
2. 法向量,决定了超平面的方向 #card=math&code=w%3D%28w_1%2Cw_2%2C%5Ccdots%2Cw_d%29)
3. 输入数据，维度为d #card=math&code=x%3D%28x_1%2Cx_2%2C%5Ccdots%2Cx_d%29)
4. 数据集 %2C(x_2%2Cy_2)%2C%5Ccdots%2C(x_d%2Cy_d)%5C%7D%2Cy_i%5Cin%5C%7B-1%2C%2B1%5C%7D#card=math&code=D%3D%5C%7B%28x_1%2Cy_1%29%2C%28x_2%2Cy_2%29%2C%5Ccdots%2C%28x_d%2Cy_d%29%5C%7D%2Cy_i%5Cin%5C%7B-1%2C%2B1%5C%7D)
5. 位移项 b

6. 样本空间任意一点x到超平面#card=math&code=%28w%5ET%2Cb%29)的距离

7. ====称为超平面的范数

3.4、原理

假设超平面#card=math&code=%28%7Bw%5ET%7D%2Cb%29)能将训练样本正确分类，即对任意的%E2%88%88D#card=math&code=%28x%7Bi%7D%2Cy%7Bi%7D%29%E2%88%88D),若，则有；若有，则有。我们令

之所以以正负1分界是为了后面计算和理解。

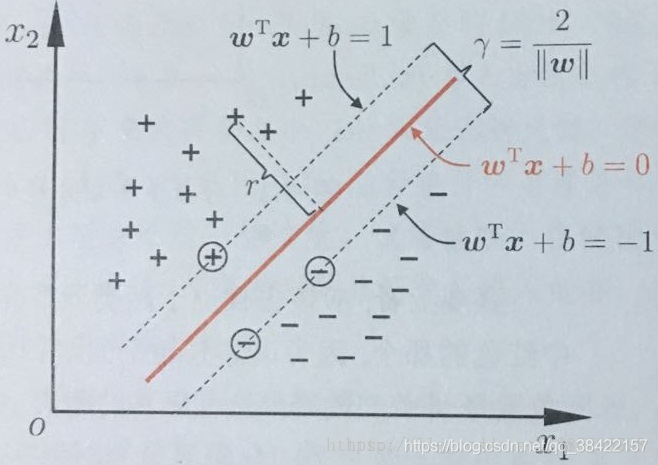
支持向量 ：在样本空间中，总会有一些正例样本和反例样本距离超平面是最近的样本点。

而过这些支持向量且平行于超平面的直线就是我们我们图中的两条直线和。两个异类支持向量到超平面的距离之和为

它被称为”间隔“(margin)。

支持向量机的目标就是找到”最大间隔“(maximum margin)的划分超平面，也就是找到能够找到满足式（3）中约束的参数w和b，使得 r 最大，即

%5Cgeq1%2Ci%3D1%2C2%2C%5Ccdots%2Cd%0A#card=math&code=max_%7Bw%2Cb%7D%20%5Cfrac%202%7B%7C%7Cw%7C%7C%7D%5C%5C%0As.t%20%5C%20%5C%20y_i%28w%5ETx_i%2Bb%29%5Cgeq1%2Ci%3D1%2C2%2C%5Ccdots%2Cd%0A)

为了最大化间隔，仅需要最大化 ，这等价于最小化 ，于是目标方程写成

%5Cgeq1%2Ci%3D1%2C2%2C%5Ccdots%2Cd%0A#card=math&code=max_%7Bw%2Cb%7D%20%5Cfrac%2012%7C%7Cw%7C%7C%5E2%5C%5C%0As.t%20%5C%20%5C%20y_i%28w%5ETx_i%2Bb%29%5Cgeq1%2Ci%3D1%2C2%2C%5Ccdots%2Cd%0A)

支持向量机的学习策略就是间隔最大化

• 对偶问题
• 核函数

• 软间隔
  • 线性可分的样本数据用硬间隔支持向量机
  • 近似线性可分用软间隔支持向量机
  • 线性不可分用核函数

支持向量回归SVR

https://blog.csdn.net/qq_38422157/article/details/88728953

4、马尔科夫

4.1、简介

对事件的全面预测，不仅要能够指出事件发生的各种可能结果，而且还必须给出每一种结果出现的概率，说明被预测的事件在预测期内出现每一种结果的可能性程度。这就是关于事件发生的概率预测。

马尔可夫（Markov)预测法，就是一种关于事件发生的概率预测方法。它是根据事件的目前状况来预测其将来各个时刻（或时期)变动状况的一种预测方法。马尔可夫预测法是地理预测研究中重要的预测方法之一

4.2、基本概念

1. 状态
   在马尔可夫预测中，“状态”是一个重要的术语。所谓状态，就是指某一事件在某个时刻（或时期)出现的某种结果。一般而言，随着所研究的事件及其预测的目标不同，状态可以有不同的划分方式。譬如，在商品销售预测中，有“畅销”、“一般”、“滞销”等状态；在农业收成预测中，有“丰收”、“平收”、“欠收”等状态；在人口构成预测中，有“婴儿”、“儿童”、“少年”、“青年”、“中年”、“老年”等状态；等等。
2. 状态转移过程
   在事件的发展过程中，从一种状态转变为另一种状态，就称为状态转移。事件的发展，随着时间的变化而变化所作的状态转移，或者说状态转移与时间的关系，就称为状态转移过程，简称过程。

3. 状态转移概率
   在事件的发展变化过程中，从某一种状态出发，下一时刻转移到其它状态的可能性，称为状态转移概率。根据条件概率的定义，由状态转为状态的状态转移概率#card=math&code=P%28Ei%E2%86%92Ej%29)就是条件概率#card=math&code=P%28Ej%2FEi%29)，即%3DP(Ej%2FEi)%3DP%7Bij%7D%0A#card=math&code=P%28E_i%E2%86%92E_j%29%3DP%28Ej%2FEi%29%3DP%7Bij%7D%0A)

4. 状态转移概率矩阵
   假定某一种被预测的事件有，共n个可能的状态。记为从状态转为状态的状态转移概率，作状态转移概率矩阵P:

4.3、原理

状态概率#card=math&code=%5Cpi_j%28k%29)

#card=math&code=%5Cpi_j%28k%29)表示事件在初始（k=0)时状态为已知的条件下，经过k次状态转移后，在第k个时刻处于状态的概率。根据概率的性质

%3D1%0A#card=math&code=%5Csum_%7Bj%3D1%7D%5EN%5Cpi_j%28k%29%3D1%0A)

从初始状态开始经过k次状态转移后到达状态这一状态转移过程，可以看作是首先经过（k-1)次状态转移的过程到达状态#card=math&code=E_i%2Ci%3D%281%2C2%2C%5Ccdots%2Cn%29)

然后在由经过一次状态转移到达状态。根据马尔科夫过程的无效性及贝叶斯条件概率公式有：

%3D%5Csum%7Bi%3D1%7D%5En%5Cpi_i(k-1)P%7Bij%7D%2C(j%3D1%2C2%2C%5Ccdots%2Cn)%0A#card=math&code=%5Cpij%28k%29%3D%5Csum%7Bi%3D1%7D%5En%5Cpii%28k-1%29P%7Bij%7D%2C%28j%3D1%2C2%2C%5Ccdots%2Cn%29%0A)

若记行向量%3D%5B%5Cpi_1(k)%2C%5Cpi_2(k)%2C%5Ccdots%2C%5Cpi_n(k)%5D#card=math&code=%5Cpi%28k%29%3D%5B%5Cpi_1%28k%29%2C%5Cpi_2%28k%29%2C%5Ccdots%2C%5Cpi_n%28k%29%5D)，则有上式可逐次计算状态概率的递推公式

%3D%5Cpi(0)P%5C%5C%0A%5Cpi(2)%3D%5Cpi(1)P%3D%5Cpi(0)P%5E2%5C%5C%0A%5Cvdots%5C%5C%0A%5Cpi(k)%3D%5Cpi(k-1)P%3D%5Cpi(0)P%5Ek%0A%0A%5Cend%7Bcases%7D%0A#card=math&code=%5Cbegin%7Bcases%7D%0A%5Cpi%281%29%3D%5Cpi%280%29P%5C%5C%0A%5Cpi%282%29%3D%5Cpi%281%29P%3D%5Cpi%280%29P%5E2%5C%5C%0A%5Cvdots%5C%5C%0A%5Cpi%28k%29%3D%5Cpi%28k-1%29P%3D%5Cpi%280%29P%5Ek%0A%0A%5Cend%7Bcases%7D%0A)

初始状态概率向量%3D%5B%5Cpi_1(0)%2C%5Cpi_2(0)%2C%5Ccdots%2C%5Cpi_n(0)%5D#card=math&code=%5Cpi%280%29%3D%5B%5Cpi_1%280%29%2C%5Cpi_2%280%29%2C%5Ccdots%2C%5Cpi_n%280%29%5D)

终极状态概率预测

经过无穷多次状态转移后所得的状态概率被称为终极状态概率，或称为平衡状态概率。

终极状态概率向量:

%0A#card=math&code=%5Cpi%3D%5B%5Cpi1%2C%5Cpi_2%2C%5Ccdots%2C%5Cpi_n%5D%5C%5C%0A%5Cpi_i%3D%5Clim%7Bk%E2%86%92%5Cinfty%7D%5Cpi_i%28k%29%0A)

即有

%3D%5Clim%7Bk%E2%86%92%5Cinfty%7D%5Cpi_i(k%2B1)%3D%5Cpi%0A#card=math&code=%5Clim%7Bk%E2%86%92%5Cinfty%7D%5Cpii%28k%29%3D%5Clim%7Bk%E2%86%92%5Cinfty%7D%5Cpi_i%28k%2B1%29%3D%5Cpi%0A)

代入递推公式可得

可得终极状态概率的条件

1. (用来计算终极状态概率)
2. 
3. 

https://blog.csdn.net/qq_41686130/article/details/81906527