BP神经网络

1、概述及原理

BP神经网络是一种按误差逆传播算法训练的多层前馈网络。

核心思想：将输出误差以某种形式通过隐层向输入层逐层反传

• 将误差分摊给各层的所有单元—各层单元的误差信号

• 修正各单元的权值。寻找合适权值w变成了一个优化问题

• 信号的正向传播

  • 输入样本—输入层—各隐层—输出层
  • 输出层实际输出与期望输出不符反向传播
  • 误差反传

• 误差的反向传播

  • 误差以某种形式在各层表示—-修正各层单元的权值
  • 网络输出的误差达到可接受的程度
  • 进行到预先设定的学习次数为止

2、bp网络特性分析

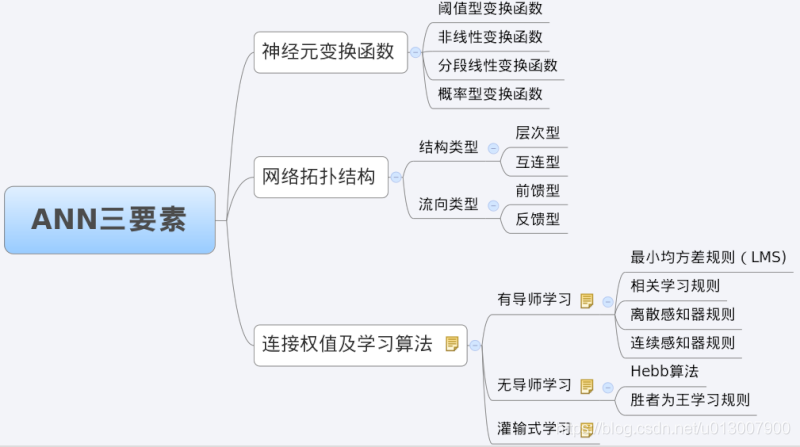
我们分析一个ANN时，通常都是从它的三要素入手，即

1. 网络拓扑结构

2. 传递函数

3. 学习算法
   

2.1、bp网络拓扑结构

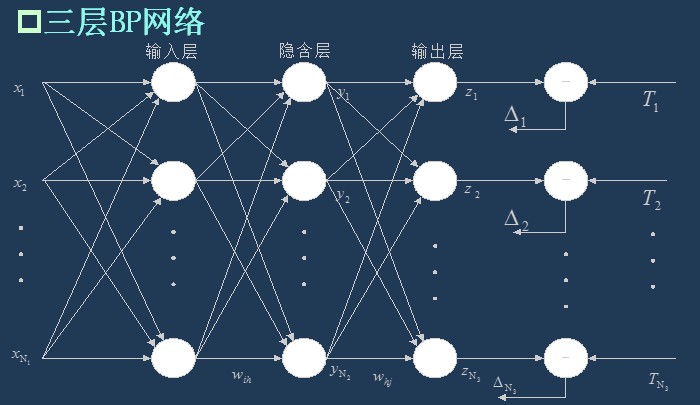
1. 网络结构：

   • 输出层有n个神经元
   • 隐含层有p个神经元
   • 输出层有q个神经元

2. 变量定义：

   • 输入变量； $ x = (x_1，x_2\cdots x_n)$

     • 输入层与中间层的连接权值
     • 隐含层各神经元的阈值
   • 隐含层输入变量 #card=math&code=hi%20%3D%20%28hi_1%EF%BC%8Chi_2%5Ccdots%20hi_p%29)

   • 隐含层输出变量 #card=math&code=ho%20%3D%20%28ho_1%EF%BC%8Cho_2%5Ccdots%20ho_p%29)

     • 隐含层与输出层的连接权值
     • 输出层各神经元的阈值
   • 输出层输入变量 )
   • 输出层输出变量 #card=math&code=yo%20%3D%20%28yo_1%EF%BC%8Cyo_2%5Ccdots%20yo_q%29)
   • 期望输出变量 #card=math&code=do%20%3D%20%28d1%EF%BC%8Cd2%5Ccdots%20dq%29)
   • 样本数据个数$ k = 1,2,\cdots m$
   • 激活函数 #card=math&code=f%28%5Ccdot%29)
   • 误差函数 -yoo(k))%5E2%7D#card=math&code=e%3D%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5E%7Bq%7D%7B%28d_o%28k%29-yo_o%28k%29%29%5E2%7D)

2.2、计算过程

1. 网络初始化

   • 给各连接权值分别赋一个区间（-1,1）内的随机数
   • 设定误差函数e
   • 给定计算精度值
   • 最大学习次数M

2. 随机选取第k个输入样本及对应的期望输出

   • %3D(x_1(k)%2Cx_2(k)%2C%5Ccdots%20x_n(k))#card=math&code=x%28k%29%3D%28x_1%28k%29%2Cx_2%28k%29%2C%5Ccdots%20x_n%28k%29%29)
   • %3D(d_1(k)%2Cd_2(k)%2C%5Ccdots%20d_q(k))#card=math&code=d_0%28k%29%3D%28d_1%28k%29%2Cd_2%28k%29%2C%5Ccdots%20d_q%28k%29%29)

3. 计算隐含层各神经元的输入和输出

   • %3D%5Csum%7Bi%3D1%7D%5Enw%7Bih%7Dxi(k)-b_h%20%5Cqquad%20h%3D1%2C2%2C%5Ccdots%2Cp#card=math&code=hi_h%28k%29%3D%5Csum%7Bi%3D1%7D%5Enw_%7Bih%7Dx_i%28k%29-b_h%20%5Cqquad%20h%3D1%2C2%2C%5Ccdots%2Cp)
   • %3Df(hi_h(k))%20%5Cqquad%20h%3D1%2C2%2C%5Ccdots%2Cp#card=math&code=ho_h%28k%29%3Df%28hi_h%28k%29%29%20%5Cqquad%20h%3D1%2C2%2C%5Ccdots%2Cp)
   • %3D%5Csum%7Bh%3D1%7D%5Epw%7Bho%7Dhoh(k))-b_o%20%5Cqquad%20o%3D1%2C2%2C%5Ccdots%2Cq#card=math&code=yi_o%28k%29%3D%5Csum%7Bh%3D1%7D%5Epw_%7Bho%7Dho_h%28k%29%29-b_o%20%5Cqquad%20o%3D1%2C2%2C%5Ccdots%2Cq)
   • %3Df(yi_o(k))%20%5Cqquad%20o%3D1%2C2%2C%5Ccdots%2Cq#card=math&code=yo_o%28k%29%3Df%28yi_o%28k%29%29%20%5Cqquad%20o%3D1%2C2%2C%5Ccdots%2Cq)
4. 利用网络期望输出和实际输出。计算误差函数对输出层的各神经元的偏导数==#card=math&code=%5Cdelta_o%28k%29)==

%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%7D%20%26%3D%20%7B%7B%5Cpartial(%7B%5Csum_h%5Ep%7Dw%7Bho%7Dhoh(k)-b_o)%7D%20%5Cover%20%5Cpartial%20w%7Bho%7D%7D%20%3D%5Ccolor%7Bblue%7D%20%7Bhoh(k)%7D%5C%5C%5C%5C%0A%0A%7B%5Ccolor%7Bgreen%7D%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20yi_o%7D%7D%20%26%3D%20%7B%5Cpartial(%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq(do(k)-yo_o(k))%5E2)%20%5Cover%20%5Cpartial%20yi_o%7D%5C%5C%0A%26%3D-(d_o(k)-yo_o(k))yo_o%5Cprime(k)%5C%5C%5C%5C%0A%26%3D-(d_o(k)-yo_o(k))f%5Cprime(yi_o(k))%5C%5C%5C%5C%0A%26%3D%5Ccolor%7Blime%7D%20-%5Cdelta_o(k)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%20%26%3D%5Ccolor%7Bgreen%7D%20%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20yio%7D%20%5Ccolor%7Bred%7D%20%7B%7B%5Cpartial%20yi_o%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%5C%5C%5C%5C%0A%0A%7B%5Ccolor%7Bred%7D%20%7B%7B%5Cpartial%20yio%28k%29%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%7D%20%26%3D%20%7B%7B%5Cpartial%28%7B%5Csumh%5Ep%7Dw%7Bho%7Dhoh%28k%29-b_o%29%7D%20%5Cover%20%5Cpartial%20w%7Bho%7D%7D%20%3D%5Ccolor%7Bblue%7D%20%7Bhoh%28k%29%7D%5C%5C%5C%5C%0A%0A%7B%5Ccolor%7Bgreen%7D%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20yi_o%7D%7D%20%26%3D%20%7B%5Cpartial%28%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq%28d_o%28k%29-yo_o%28k%29%29%5E2%29%20%5Cover%20%5Cpartial%20yi_o%7D%5C%5C%0A%26%3D-%28d_o%28k%29-yo_o%28k%29%29yo_o%5Cprime%28k%29%5C%5C%5C%5C%0A%26%3D-%28d_o%28k%29-yo_o%28k%29%29f%5Cprime%28yi_o%28k%29%29%5C%5C%5C%5C%0A%26%3D%5Ccolor%7Blime%7D%20-%5Cdelta_o%28k%29%0A%5Cend%7Baligned%7D%0A)

1. 利用隐含层到输出层的连接权值、输出层的==#card=math&code=%5Cdeltao%28k%29)和隐含层的输出计算误差函数对隐含层各神经元的偏导数#card=math&code=%5Cdelta_h%28k%29)== %20%5Ccolor%7Bblue%7D%20ho_h(k)%5C%5C%5C%5C%0A%0A%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20w%7Bih%7D%7D%20%0A%26%3D%20%5Ccolor%7Blime%7D%7B%7B%5Cpartial%20e%7D%20%5Cover%20%7B%5Cpartial%20hih(k)%7D%7D%20%5Ccolor%7Bblue%7D%7B%7B%5Cpartial%20hi_h(k)%7D%20%5Cover%20%7B%5Cpartial%20w%7Bih%7D%7D%7D%5C%5C%5C%5C%0A%0A%5Ccolor%7Bblue%7D%7B%7B%5Cpartial%20hih(k)%7D%20%5Cover%20%7B%5Cpartial%20w%7Bih%7D%7D%7D%0A%26%3D%7B%5Cpartial(%5Csum%7Bi%3D1%7D%5En%20w%7Bih%7Dxi(k)-b_h)%20%5Cover%20%5Cpartial%20w%7Bih%7D%7D%0A%3Dxi(k)%5C%5C%5C%5C%0A%0A%5Ccolor%7Blime%7D%7B%7B%5Cpartial%20e%7D%20%5Cover%20%7B%5Cpartial%20hi_h(k)%7D%7D%0A%26%3D%7B%5Cpartial(%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq(do(k)-yo_o(k))%5E2)%20%5Cover%20%5Cpartial%20ho_h(k)%7D%20%7B%5Cpartial%20ho_h(k)%5Cover%5Cpartial%20hi_h(k)%7D%5C%5C%5C%5C%0A%26%3D%7B%5Cpartial(%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq(do(k)-f(yi_o(k)))%5E2)%5Cover%5Cpartial%20ho_h(k)%7D%20%7B%5Cpartial%20ho_h(k)%5Cover%5Cpartial%20hi_h(k)%7D%5C%5C%5C%5C%0A%26%3D%7B%5Cpartial(%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq((do(k)-f(%5Csum%7Bh%3D1%7D%5Epw%7Bho%7Dho_h(k)-b_o)%5E2))%5Cover%5Cpartial%20ho_h(k)%7D%20%7B%5Cpartial%20%20%20%20%20%20%20%20%20ho_h(k)%5Cover%5Cpartial%20hi_h(k)%7D%5C%5C%5C%5C%0A%26%3D-%5Csum%7Bo%3D1%7D%5Eq(do(k)-yo_o(k))f%5Cprime(yi_o(k))w%7Bho%7D%7B%5Cpartial%20hoh(k)%5Cover%5Cpartial%20hi_h(k)%7D%5C%5C%5C%5C%0A%26%3D-(%5Csum%7Bo%3D1%7D%5Eq%5Cdeltao(k)w%7Bho%7D)f%5Cprime(hih(k))%3D-%5Cdelta_h(k)%0A%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%20%0A%26%3D%7B%5Ccolor%7Bgreen%7D%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20yio%7D%7D%20%7B%5Ccolor%7Bred%7D%7B%7B%5Cpartial%20yi_o%7D%5Cover%20%5Cpartial%20w%7Bho%7D%7D%7D%20%0A%3D%20%5Ccolor%7Blime%7D%20-%5Cdeltao%28k%29%20%5Ccolor%7Bblue%7D%20ho_h%28k%29%5C%5C%5C%5C%0A%0A%7B%7B%5Cpartial%20e%7D%5Cover%20%5Cpartial%20w%7Bih%7D%7D%20%0A%26%3D%20%5Ccolor%7Blime%7D%7B%7B%5Cpartial%20e%7D%20%5Cover%20%7B%5Cpartial%20hih%28k%29%7D%7D%20%5Ccolor%7Bblue%7D%7B%7B%5Cpartial%20hi_h%28k%29%7D%20%5Cover%20%7B%5Cpartial%20w%7Bih%7D%7D%7D%5C%5C%5C%5C%0A%0A%5Ccolor%7Bblue%7D%7B%7B%5Cpartial%20hih%28k%29%7D%20%5Cover%20%7B%5Cpartial%20w%7Bih%7D%7D%7D%0A%26%3D%7B%5Cpartial%28%5Csum%7Bi%3D1%7D%5En%20w%7Bih%7Dxi%28k%29-b_h%29%20%5Cover%20%5Cpartial%20w%7Bih%7D%7D%0A%3Dxi%28k%29%5C%5C%5C%5C%0A%0A%5Ccolor%7Blime%7D%7B%7B%5Cpartial%20e%7D%20%5Cover%20%7B%5Cpartial%20hi_h%28k%29%7D%7D%0A%26%3D%7B%5Cpartial%28%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq%28do%28k%29-yo_o%28k%29%29%5E2%29%20%5Cover%20%5Cpartial%20ho_h%28k%29%7D%20%7B%5Cpartial%20ho_h%28k%29%5Cover%5Cpartial%20hi_h%28k%29%7D%5C%5C%5C%5C%0A%26%3D%7B%5Cpartial%28%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq%28do%28k%29-f%28yi_o%28k%29%29%29%5E2%29%5Cover%5Cpartial%20ho_h%28k%29%7D%20%7B%5Cpartial%20ho_h%28k%29%5Cover%5Cpartial%20hi_h%28k%29%7D%5C%5C%5C%5C%0A%26%3D%7B%5Cpartial%28%7B1%5Cover2%7D%5Csum%7Bo%3D1%7D%5Eq%28%28do%28k%29-f%28%5Csum%7Bh%3D1%7D%5Epw%7Bho%7Dho_h%28k%29-b_o%29%5E2%29%29%5Cover%5Cpartial%20ho_h%28k%29%7D%20%7B%5Cpartial%20%20%20%20%20%20%20%20%20ho_h%28k%29%5Cover%5Cpartial%20hi_h%28k%29%7D%5C%5C%5C%5C%0A%26%3D-%5Csum%7Bo%3D1%7D%5Eq%28do%28k%29-yo_o%28k%29%29f%5Cprime%28yi_o%28k%29%29w%7Bho%7D%7B%5Cpartial%20hoh%28k%29%5Cover%5Cpartial%20hi_h%28k%29%7D%5C%5C%5C%5C%0A%26%3D-%28%5Csum%7Bo%3D1%7D%5Eq%5Cdeltao%28k%29w%7Bho%7D%29f%5Cprime%28hi_h%28k%29%29%3D-%5Cdelta_h%28k%29%0A%0A%5Cend%7Baligned%7D%0A)

1. 利用输出层各神经元的==#card=math&code=%5Cdeltao%28k%29)和隐含层各神经元的输出来修正连接权值#card=math&code=W%7Bho%7D%28k%29)==。 %20%26%3D%20-%5Cmu%7B%5Cpartial%20e%5Cover%20%5Cpartial%20w%7Bho%7D%7D%3D%5Cmu%5Cdelta_o(k)ho_h(k)%5C%5C%5C%5C%0A%0AW%7Bho%7D%5E%7BN%2B1%7D%20%26%3D%20W%7Bho%7D%5EN%20%2B%20%5Ceta%5Cdelta_o(k)ho_h(k)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5CDelta%20W%7Bho%7D%28k%29%20%26%3D%20-%5Cmu%7B%5Cpartial%20e%5Cover%20%5Cpartial%20w%7Bho%7D%7D%3D%5Cmu%5Cdelta_o%28k%29ho_h%28k%29%5C%5C%5C%5C%0A%0AW%7Bho%7D%5E%7BN%2B1%7D%20%26%3D%20W_%7Bho%7D%5EN%20%2B%20%5Ceta%5Cdelta_o%28k%29ho_h%28k%29%0A%5Cend%7Baligned%7D%0A)

1. 利用隐含层各神经元的==#card=math&code=%5Cdeltah%28k%29)==和输入层各神经元的输入修正连接权值。 %20%26%3D%20-%5Cmu%7B%5Cpartial%20e%5Cover%20%5Cpartial%20w%7Bih%7D%7D%0A%3D-%5Cmu%7B%5Cpartial%20e%20%5Cover%20%5Cpartial%20hi_h(k)%7D%7B%5Cpartial%20hi_h(k)%20%5Cover%5Cpartial%20W%7Bih%7D%7D%0A%3D%5Cdeltah(k)x_i(k)%5C%5C%5C%5C%0A%0AW%7Bih%7D%5E%7BN%2B1%7D%20%26%3D%20W%7Bih%7D%5EN%20%2B%20%5Ceta%5Cdelta_h(k)x_i(k)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5CDelta%20W%7Bih%7D%28k%29%20%26%3D%20-%5Cmu%7B%5Cpartial%20e%5Cover%20%5Cpartial%20w%7Bih%7D%7D%0A%3D-%5Cmu%7B%5Cpartial%20e%20%5Cover%20%5Cpartial%20hi_h%28k%29%7D%7B%5Cpartial%20hi_h%28k%29%20%5Cover%5Cpartial%20W%7Bih%7D%7D%0A%3D%5Cdeltah%28k%29x_i%28k%29%5C%5C%5C%5C%0A%0AW%7Bih%7D%5E%7BN%2B1%7D%20%26%3D%20W_%7Bih%7D%5EN%20%2B%20%5Ceta%5Cdelta_h%28k%29x_i%28k%29%0A%5Cend%7Baligned%7D%0A)

1. 计算全局误差 -yo(k))%5E2%0A#card=math&code=E%3D%7B1%5Cover2m%7D%5Csum%7Bk%3D1%7D%5Em%5Csum_%7Bo%3D1%7D%5Eq%28d_o%28k%29-y_o%28k%29%29%5E2%0A)

1. 判断网络误差是否满足要求

   • 误差达到预设精度
   • 学习次数大于设定的最大次数

否则，选取下一个学习样本及对应的期望输出，返回到第三步，进入下一轮学习