考虑走到某一个终点[i][j]的前一步有哪几种情况

64. 最小路径和

  1. class Solution {
  2.     public int minPathSum(int[][] grid) {
  3.         if(grid.length==0) return 0;
  4.         int m=grid.length;
  5.         int n=grid[0].length;
  6.         int[][] dp=new int[m][n];
  7.         dp[0][0]=grid[0][0];
  8.         for(int i=1;i<m;i++){
  9.             dp[i][0]=dp[i-1][0]+grid[i][0];
  10.         }
  11.         for(int j=1;j<n;j++){
  12.             dp[0][j]=dp[0][j-1]+grid[0][j];
  13.         }
  14.         for(int i=1;i<m;i++){
  15.             for(int j=1;j<n;j++){
  16.                 dp[i][j]=Math.min(dp[i][j-1],dp[i-1][j])+grid[i][j];
  17.             }
  18.         }
  19.         return dp[m-1][n-1];
  20.     }
  21. }

931. 下降路径最小和

题解
dp[i][j]表示落到matrix[i][j]这个点的最小路径和。
首先,终点可能在最后一行的任意一列

  1.     for (int j = 0; j < n; j++) {
  2.         res = Math.min(res, dp[n-1][j]);
  3.     }

其次，因为只能从相邻列下落，所以每个格子只能从上一行的三个或两个（边界）获取前一步的最小值。如下图：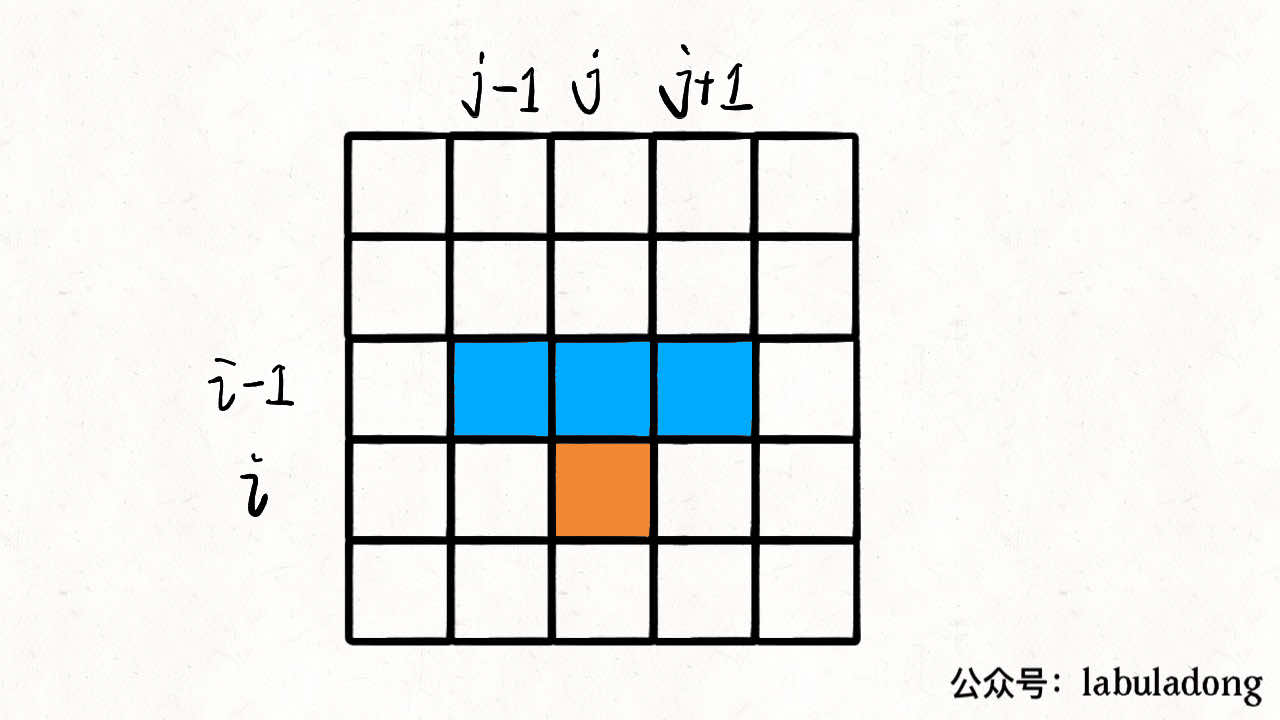
最小路径 - 图1

  1. class Solution {
  2.     public int minFallingPathSum(int[][] matrix) {
  3.         int n=matrix.length;
  4.         if(n==1) return matrix[0][0];
  5.         int[][] dp=new int[n][n];
  6.         int res=Integer.MAX_VALUE;
  7.         for(int j=0;j<n;j++){
  8.             dp[0][j]=matrix[0][j];
  9.         }
  10.         for(int i=1;i<n;i++){
  11.             for(int j=0;j<n;j++){
  12.                 dp[i][j]=getMin(i,j,dp,n)+matrix[i][j];
  13.                 if(i==n-1){
  14.                     res=Math.min(res,dp[i][j]);
  15.                 }
  16.             }
  17.         }
  18.         return res;
  19.     }
  21.     public int getMin(int i,int j,int[][] dp,int n){
  22.         if(j-1<0){
  23.             return Math.min(dp[i-1][j],dp[i-1][j+1]);
  24.         }else if(j+1>=n){
  25.             return Math.min(dp[i-1][j-1],dp[i-1][j]);
  26.         }else{
  27.             return Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i-1][j+1]));
  28.         }
  29.     }
  30. }

72. 编辑距离

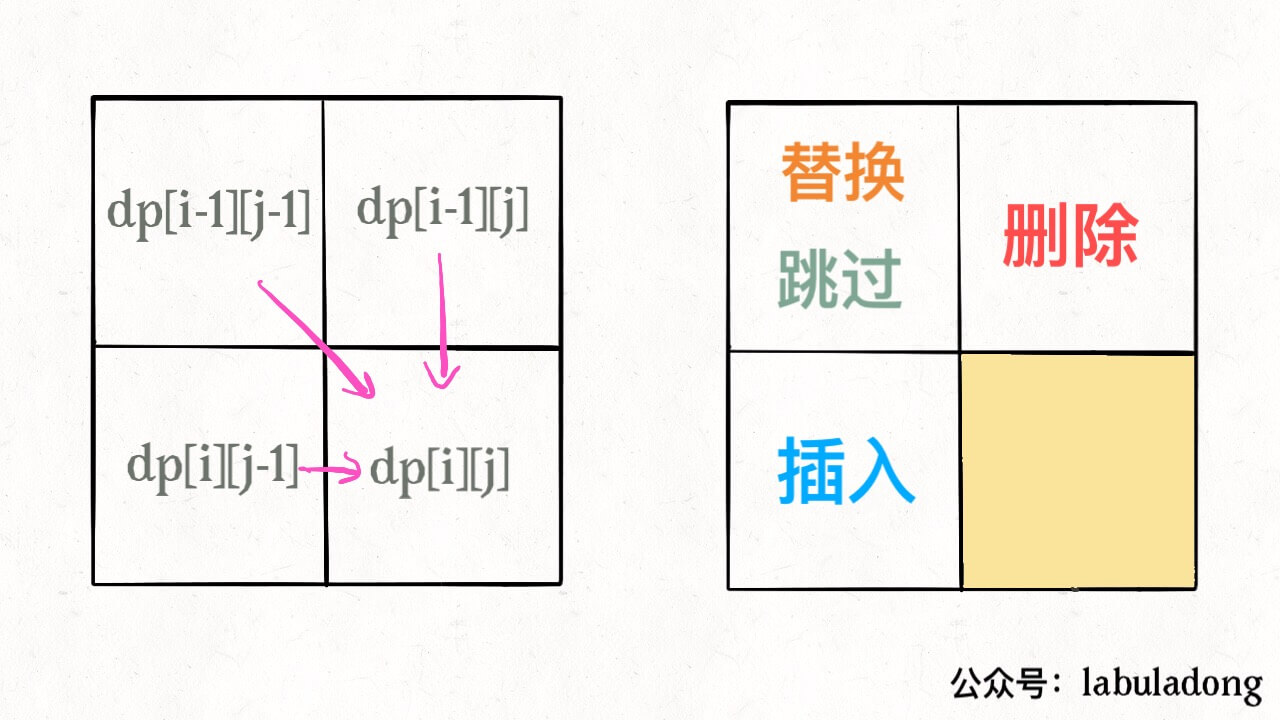
最小路径 - 图2

  1. class Solution {
  2.   public int minDistance(String word1, String word2) {
  3.     int l1=word1.length();
  4.     int l2=word2.length();
  5.     int[][] dp =new int[l1+1][l2+1];
  6.     for(int i=1;i<=l1;i++){
  7.       dp[i][0]=dp[i-1][0]+1;
  8.     }
  9.     for(int j=1;j<=l2;j++){
  10.       dp[0][j]=dp[0][j-1]+1;
  11.     }
  12.     for(int i=1;i<=l1;i++){
  13.       for(int j=1;j<=l2;j++){
  14.         if(word1.charAt(i-1)==word2.charAt(j-1)){
  15.           dp[i][j]=dp[i-1][j-1];
  16.         }else{
  17.           dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1;
  18.         }
  19.       }
  20.     }
  21.     return dp[l1][l2];
  22.   }
  23. }