寻找重复的子树

通过序列化树结构，结合HashSet，来判断是否重复
（1）如果能加入set说明是第一次出现，如果不能加入set但是能加入resSet说明是第二次出现，无法加入set和resSet说明出现两次以上。返回结果不重复。
（2）还有序列化的顺序：注意，不能使用中序遍历
测试用例：[0,0,0,0,null,null,0,null,null,null,0]
如果采用中序遍历，那么左子树是#0#0#，右子树的右子树也是#0#0#
采用前序遍历，那么左子树是00###，右子树是0#0##
采用后序遍历，那么左子树是#0##0，右子树是##0#0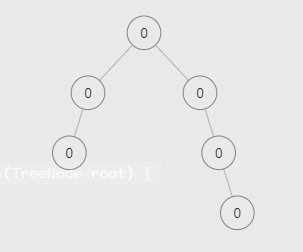

class Solution {
  HashSet<String> set = new HashSet<>();
  List<TreeNode> res = new ArrayList<>();
  HashSet<String> resSet = new HashSet<>();
  public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
    findHelper(root);
    return res;
  }
  public String findHelper(TreeNode root) {
    if (root == null) return "#";
    String left = findHelper(root.left);
    String right = findHelper(root.right);
    StringBuilder sb = new StringBuilder();
    //注意这里的顺序
    sb.append(root.val).append(",").append(left).append(",").append(right);
    if(!set.add(sb.toString())&&resSet.add(sb.toString())){
      res.add(root);
    }
    return sb.toString();
  }
}

二叉搜索树

疯狂递归

判断BST的合法性

不可以仅仅判断每个节点的左子节点小于该节点，右子节点大于该节点。因为以根为界，右子树的左子树也不能小于根节点的数值，每个节点都有一个范围。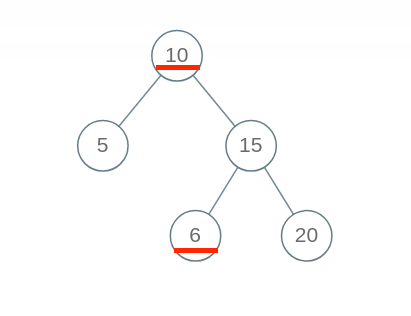
二叉树 - 图2

boolean isValidBST(TreeNode root) {
    return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
    // base case
    if (root == null) return true;
    // 若 root.val 不符合 max 和 min 的限制，说明不是合法 BST
    if (min != null && root.val <= min.val) return false;
    if (max != null && root.val >= max.val) return false;
    // 限定左子树的最大值是 root.val，右子树的最小值是 root.val
    return isValidBST(root.left, min, root) 
        && isValidBST(root.right, root, max);
}

在二叉树中插入一个值

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root==null) return new TreeNode(val);
        if(root.val>val){
            root.left=insertIntoBST(root.left,val);
        }else{
            root.right=insertIntoBST(root.right,val);
        }
        return root;
    }
}

在二叉搜索树中搜索一个值

返回以它为根节点的子树

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null) return null;
        if(root.val==val) return root;
        else if(root.val<val) return searchBST(root.right, val);
        else return searchBST(root.left,val);
    }
}

在二叉树中删除一个值

需要注意如何处理左右子树都不为空的情况

 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return null;
        if(root.val==key){
            if(root.left==null&&root.right==null) return null;
            if(root.left==null&&root.right!=null) return root.right;
            if(root.left!=null&&root.right==null) return root.left;
            if(root.left!=null&&root.right!=null){
                //找到右边最小的节点或左边最大的节点
                TreeNode min=findMin(root.right);
                root.val=min.val;
                root.right=deleteNode(root.right, min.val);
            }
        }else if(root.val>key){
            root.left=deleteNode(root.left, key);
        }else{
            root.right=deleteNode(root.right, key);
        }
        return root;
    }

    private TreeNode findMin(TreeNode node){
        if(node.left!=null) node=findMin(node.left);
        return node;
    }
}

【困难】二叉搜索子树的最大键值和

链接
 题目

class Solution {
    int sum=0;
    public int maxSumBST(TreeNode root) {
        if(root==null) return 0;
        maxSumBSTHelper(root);
        return sum;
    }

    public int[] maxSumBSTHelper(TreeNode root){
        if(root==null){
            //isBST,min,max,sum
            return new int[]{1,Integer.MAX_VALUE,Integer.MIN_VALUE,0};
        }
        int[] left=maxSumBSTHelper(root.left);
        int[] right=maxSumBSTHelper(root.right);
        int[] res=new int[4];
        if(left[0]==1&&right[0]==1&&root.val>left[2]&&root.val<right[1]){
            res[0]=1;
            res[1]=Math.min(left[1],root.val);
            res[2]=Math.max(right[2],root.val);
            res[3]=left[3]+right[3]+root.val;
            sum=Math.max(res[3],sum);
        }else{
            res[0]=0;
        }
        return res;
    }
}

【困难】二叉树的序列化和反序列化

使用递归

这里用的先序遍历，也可以用后序遍历，但是不可以用中序遍历，原因和寻找重复子树里出现的问题相似。

public class Codec {
  private int index=0;
  private static final String ISNULL="#";
  private static final String SEP=",";

    // Encodes a tree to a single string.
  public String serialize(TreeNode root) {
    StringBuffer sb=new StringBuffer();
    serializeHelper(root,sb);
    return sb.toString();
  }

  private void serializeHelper(TreeNode root,StringBuffer sb){
    if(root==null){
      sb.append(ISNULL).append(SEP);
      return;
    }
    sb.append(root.val).append(SEP);
    serializeHelper(root.left,sb);
    serializeHelper(root.right,sb);
  }

    // Decodes your encoded data to tree.
  public TreeNode deserialize(String data) {
    String[] datas=data.split(SEP);
    return deserializeHelper(datas);
  }

  private TreeNode deserializeHelper(String[] datas){
    if(index==datas.length) return null;
    String str=datas[index++];
    if(str.equals(ISNULL)) return null;
    TreeNode root=new TreeNode(Integer.parseInt(str));
    root.left=deserializeHelper(datas);
    root.right=deserializeHelper(datas);
    return root;
  }
}

使用栈

public class Codec {

    // Encodes a tree to a single string.
  public String serialize(TreeNode root) {
    StringBuilder sb = new StringBuilder();
    if (root == null) {
      return sb.toString();
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
      TreeNode node = queue.poll();
      if (sb.length() != 0) {
        sb.append(",");
      }
      if (node != null) {
        sb.append(node.val);
        queue.offer(node.left);
        queue.offer(node.right);
      } else {
        sb.append("null");
      }
    }
    return sb.toString();
  }

    // Decodes your encoded data to tree.
  public TreeNode deserialize(String data) {
    if (data.length() == 0) return null;
    String[] strings = data.split(",");
    TreeNode root = new TreeNode(Integer.valueOf(strings[0]));
    TreeNode node = root;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(node);
    for (int i = 1; i < strings.length;) {
      node=queue.poll();
      String leftVal = strings[i++];
      if(leftVal.equalsIgnoreCase("null")){
        node.left=null;
      }else{
        TreeNode leftNode=new TreeNode(Integer.valueOf(leftVal));
        queue.offer(leftNode);
        node.left=leftNode;
      }
      String rightVal = strings[i++];
      if(rightVal.equalsIgnoreCase("null")){
        node.right=null;
      }else{
        TreeNode rightNode=new TreeNode(Integer.valueOf(rightVal));
        queue.offer(rightNode);
        node.right=rightNode;
      }
    }
    return root;
  }
}

二叉树的最近公共祖先

lowestCommonAncestor（root,p,q）这个函数，如果以root为根节点的树里面既没有p也没有q返回null。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null||p==root||q==root) return root;
        TreeNode left=lowestCommonAncestor(root.left,p,q);
        TreeNode right=lowestCommonAncestor(root.right, p, q);
        if(left!=null&&right!=null) return root;
        if(left!=null) return left;
        if(right!=null) return right;
        return null;
    }
}

完全二叉树的节点个数

计算二叉树的节点个数可以用下面代码，时间复杂度O(N）

    public int countNodes(TreeNode root) {
        if(root==null) return 0;
        return 1+countNodes(root.left)+countNodes(root.right);
    }

完全二叉树的话需要利用完全二叉树的性质，时间复杂度O(logN*logN)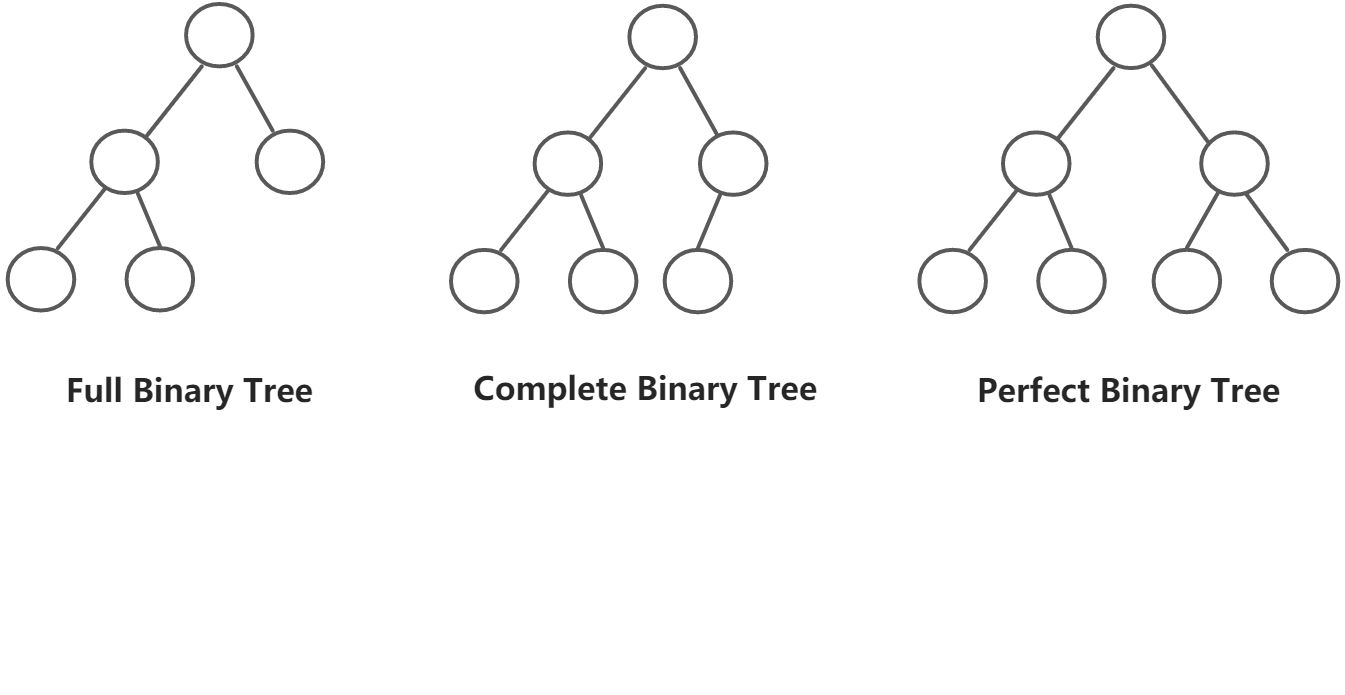
二叉树 - 图3

class Solution {
    public int countNodes(TreeNode root) {
        if(root==null) return 0;
        int left=0,right=0;
        TreeNode node=root;
        while(node!=null){
            left++;
            node=node.left;
        }
        node=root;
        while(node!=null){
            right++;
            node=node.right;
        }
        if(left==right) return (int)Math.pow(2,left)-1;
        else return 1+countNodes(root.left)+countNodes(root.right);
    }
}

二叉树