要点:存在最优子结构,能够通过子问题的最值得到原问题的最值。
不是所有的最长最短最佳XXX都是动态规划
背包问题
零钱系列
322. 零钱兑换
这个不是背包吧,但是写在这里好了。
给出零钱组合coins[],要求计算出凑amount元最少需要多少硬币。
class Solution {public int coinChange(int[] coins, int amount) {if(amount==0||coins.length==0) return 0;int[] dp=new int[amount+1];dp[0]=0;for(int i=1;i<=amount;i++){int count=amount+1;for(int coin:coins){if(coin>i) continue;count=Math.min(count,dp[i-coin]+1);}dp[i]=count;}return dp[amount]==amount+1?-1:dp[amount];}}
面试题 08.11. 硬币
硬币可以多次使用,计算凑amount元有多少种方式。
注意这个循环的遍历,需要把coin放在外层,因为5+2+1和1+2+5是相同的方法。
class Solution {public int change(int amount, int[] coins) {int[] dp=new int[amount+1];dp[0]=1;for(int coin:coins){for(int i=0;i<=amount;i++){if(coin>i) continue;dp[i]+=dp[i-coin];}}return dp[amount];}}
279. 完全平方数
和硬币的问题很像
本来用的dfs来解这个题,结果在输入n=260的时候就超出时间限制了。
class Solution {public int numSquares(int n) {List<Integer> squares=new ArrayList<>();int[] dp=new int[n+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0]=0;int cur=1;while(cur*cur<=n){int k=cur*cur;for(int i=1;i<=n;i++){if(i>=k){dp[i]=Math.min(dp[i],dp[i-k]+1);}}cur++;}return dp[n];}}
494. 目标和
我觉得是背包,嗯
和上一题类似,要用给定数组中的数字来凑成目标值。不过是改成了“每种硬币只能用一次”的情况,所以遍历的代码发生了改变,要从后往前。
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int n:nums) sum+=n;if((target+sum)%2!=0) return 0;int k=(target+sum)/2;int[] dp=new int[k+1];dp[0]=1;for(int n:nums){for(int i=k;i>=n;i--){dp[i]+=dp[i-n];}//其实是这样//for(int i=k;i>0;i--){// if(i<n) break;// else dp[i]+=dp[i-n];//}}return dp[k];}}
其他
152. 乘积最大子数组
保存每一步的最大值和最小值,因为有正数也有负数
注意对0的处理。
class Solution {public int maxProduct(int[] nums) {int res=Integer.MIN_VALUE;int max=1,min=1;for(int num:nums){if(num==0){res=Math.max(res,0);min=1;max=1;}else{if(num<0){int temp=min;min=max;max=temp;}min=Math.min(min*num,num);max=Math.max(max*num,num);res=Math.max(res,max);}}return res;}}
264. 丑数 II
用三指针解决,很巧妙。
注意下面的判断,都是if,不能用if—else,那样会有重复的数字,比如123和132。
dp[i]表示第i+1个丑数
class Solution {public int nthUglyNumber(int n) {int[] dp=new int[n];dp[0]=1;int i2=0,i3=0,i5=0;for(int i=1;i<n;i++){dp[i]=Math.min(Math.min(dp[i2]*2,dp[i3]*3),dp[i5]*5);if(dp[i]==dp[i2]*2) i2++;if(dp[i]==dp[i3]*3) i3++;if(dp[i]==dp[i5]*5) i5++;}return dp[n-1];}}
204. 计数质数
埃氏筛
如果一个数x是质数,那么2x,3x…都不是质数。
以我的脑子肯定觉得是从j=i+i开始,但是题解里面是j=ii,可以提高效率。
另外:注意ii可能越界,所以要用(long)做一下类型转换。
class Solution {public int countPrimes(int n) {int count = 0;if (n < 3) {return count;}boolean[] isPrime=new boolean[n];Arrays.fill(isPrime, true);for (int i = 2; i < n; i++) {if (isPrime[i]){count++;if((long)i*i<n){for(int j=i*i;j<n;j=j+i){isPrime[j]=false;}}}}return count;}}
博弈问题
877. 石子游戏

用了一个三维数组来做动态规划,结果效率很低。
前提:两人都聪明
piles=[5,3,4,5]
dp[i][j][0]表示用数组中下标i-j的石子来比赛,先手获得的分数
dp[i][j][1]表示用数组中下标i-j的石子来比赛,后手获得的分数
所以动态规划的base case:
dp[i][i][0]=piles[i]
dp[i][i][1]=0
即当只有一堆石子的时候,先手获得的分数是这堆石头的个数,而后手是0分
动态转移方程:
dp[i][j][0]=Math.max(piles[i]+dp[i+1][j][1], piles[j]+dp[i][j-1][1]);
选择最左边石头最终的分数,选择最右边石头最终的分数
如果先手选择了左边,那么后手获得的分数就是剩下右边一堆先手获得的分数
dp[i][j][1]=dp[i+1][j][0]
如果先手选择了右边
dp[i][j][1]=dp[i][j-1][0]
class Solution {public boolean stoneGame(int[] piles) {int n=piles.length;int[][][] dp=new int[n][n][2];for(int i=0;i<n;i++){dp[i][i][0]=piles[i];dp[i][i][1]=0;}for(int i=n-2;i>=0;i--){for(int j=i+1;j<n;j++){int left = piles[i]+dp[i+1][j][1];int right = piles[j]+dp[i][j-1][1];if(left>right){//先手dp[i][j][0]=left;//后手dp[i][j][1]=dp[i+1][j][0];}else{dp[i][j][0]=right;dp[i][j][1]=dp[i][j-1][0];}}}return dp[0][n-1][0]-dp[0][n-1][1]>0;}}
292. Nim 游戏

找规律,如果剩下1-3块石头就是自己胜出,如果剩下4块石头(无论拿走多少,都给对方剩下1-3块)就是对方胜出。
比如剩下的石头是5块,我可以拿走1个,那么对方剩下4块,他就无法获胜。
所以:
class Solution {public boolean canWinNim(int n) {return n%4!=0;}}
887. 鸡蛋掉落
题目:有 K 个鸡蛋,有 N 层楼,用最少的操作次数 F 检查出鸡蛋的质量。(找到蛋最低在第几层楼下落会碎,测试的时候蛋没碎可以再用)
题解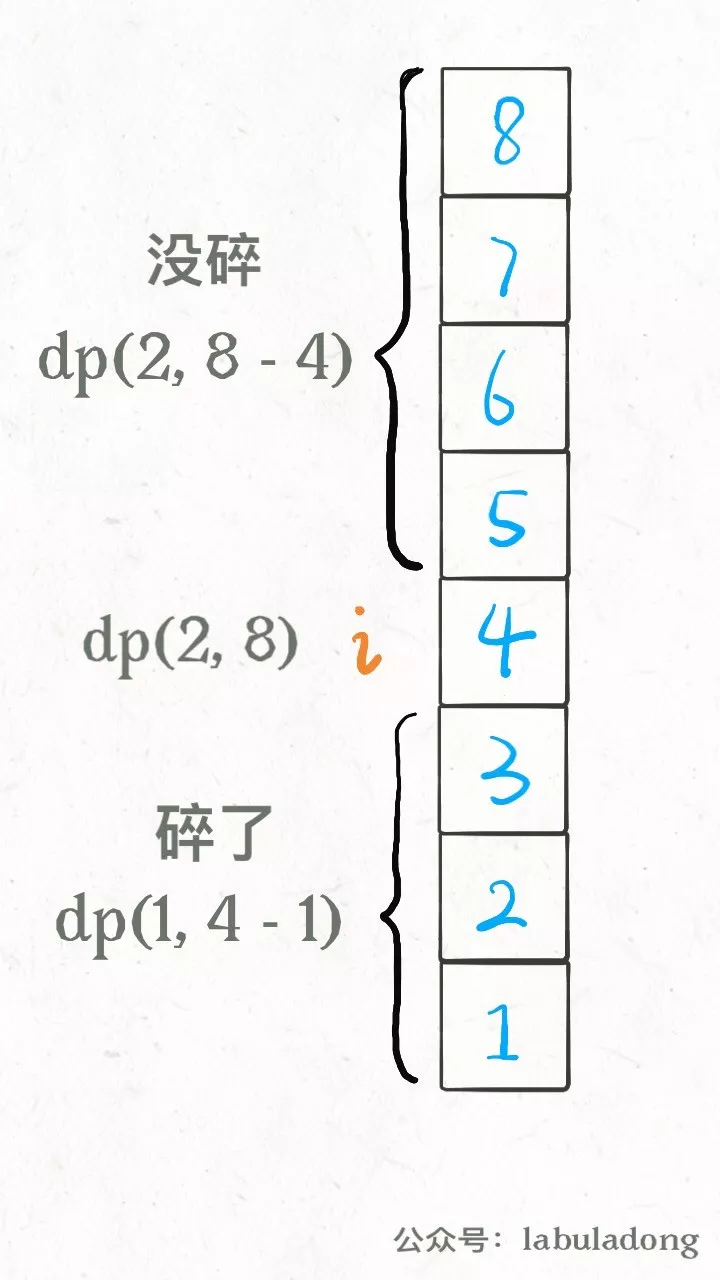
相对容易理解的思路:
dp[i][j]:表示i个鸡蛋,j层楼,至少测dp[i][j]次可以找到鸡蛋会破的那层楼。
res=Math.min(res,Math.max(dp[i-1][p-1],dp[i][j-p])+1);
max(破了所以测下面的楼层,没破所以测上面的楼层)+1(这次用掉的次数)
但是会超时
class Solution {
public int superEggDrop(int k, int n) {
if(n==1) return 1;
if(k==1) return n;
int[][] dp=new int[k+1][n+1];
for(int i=1;i<=k;i++){
dp[i][1]=1;
}
for(int j=1;j<=n;j++){
dp[1][j]=j;
}
for(int i=2;i<=k;i++){
for(int j=2;j<=n;j++){
int res=Integer.MAX_VALUE;
for(int p=1;p<=j;p++){
res=Math.min(res,Math.max(dp[i-1][p-1],dp[i][j-p])+1);
}
dp[i][j]=res;
}
}
return dp[k][n];
}
}
用二分查找优化最内层
题解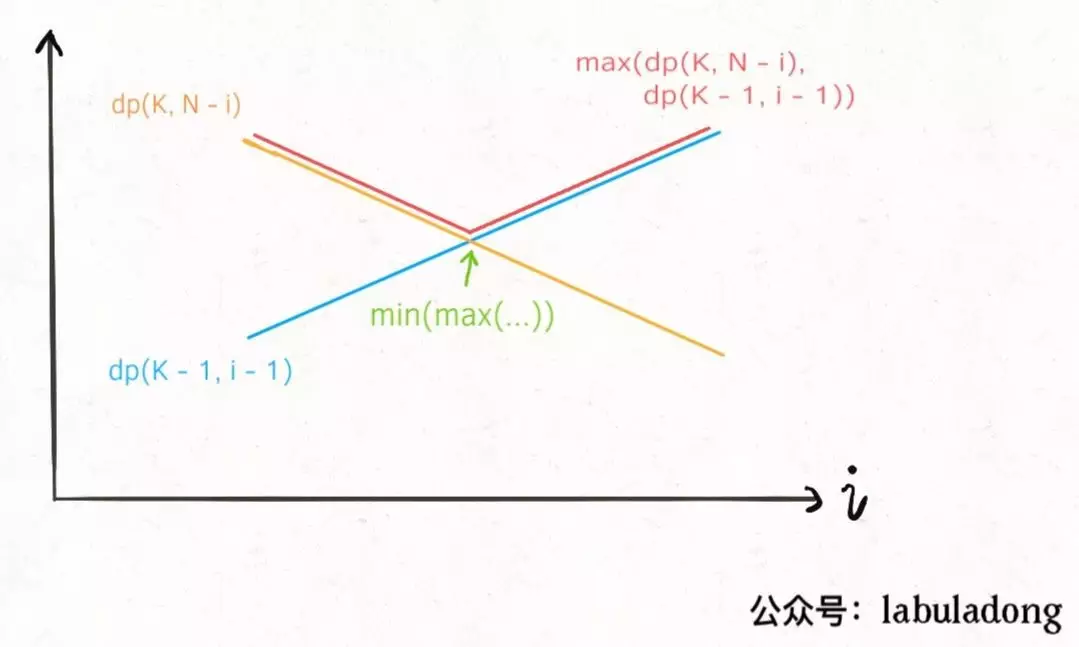
class Solution {
public int superEggDrop(int k, int n) {
if(n==1) return 1;
if(k==1) return n;
int[][] dp=new int[k+1][n+1];
for(int i=1;i<=k;i++){
dp[i][1]=1;
}
for(int j=1;j<=n;j++){
dp[1][j]=j;
}
for(int i=2;i<=k;i++){
for(int j=2;j<=n;j++){
int res=Integer.MAX_VALUE;
int low=1,high=j;
while(low<=high){
int mid=low+(high-low)/2;
int broken=dp[i-1][mid-1];
int not_broken=dp[i][j-mid];
if(broken>not_broken){
high=mid-1;
res=Math.min(res,broken+1);
}else if(broken<not_broken){
low=mid+1;
res=Math.min(res,not_broken+1);
}else{
res=Math.min(res,broken+1);
break;
}
}
dp[i][j]=res;
}
}
return dp[k][n];
}
}
大佬的方法:
(不是很明白)
本题逆向思维,若你有 K 个鸡蛋,你最多操作M次,求 N 最大值。
dp[k][m]=1+dp[k-1][m-1]+dp[k][m-1];
1是你这次扔鸡蛋的这层楼。
dp[k-1][m-1]表示如果这次扔鸡蛋破了,那么只剩下k-1个鸡蛋和m-1次扔鸡蛋的机会可以探测到的最高楼层数。
dp[k][m-1]表示这次扔鸡蛋没有破,还剩下k个鸡蛋和m-1次扔鸡蛋机会可以探测到的最高楼层数。
class Solution {
public int superEggDrop(int k, int n) {
int[][] dp=new int[k+1][n+1];
int m=0;
while(dp[k][m]<n){
m++;
for(int i=1;i<=k;i++){
dp[i][m]=1+dp[i-1][m-1]+dp[i][m-1];
}
}
return m;
}
}
10. 正则表达式匹配
如果把字符串存到array中会快一点点
public class Solution {
public boolean isMatch(String s, String p) {
int slen = s.length();
int plen = p.length();
if (p.equalsIgnoreCase(".*")) return true;
if (plen == 0) {
if (slen == 0) return true;
else return false;
} else if (slen == 0) {
if (countAsterisk(p) * 2 == p.length()) return true;
else return false;
}
//长度都不为0
boolean[][] dp = new boolean[slen + 1][plen + 1];
dp[0][0] = true;
//初始化s=0
for (int j = 1; j <= plen; j++) {
if (j == 1) dp[0][j] = false;
if (p.charAt(j - 1) == '*' && dp[0][j - 2]) dp[0][j] = true;
}
//判断后续的字符
for (int i = 1; i <= slen; i++) {
for (int j = 1; j <= plen; j++) {
if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
}
//如果是*号
else if (p.charAt(j - 1) == '*') {
if (j == 1) dp[i][j] = false;
if (p.charAt(j - 2) == s.charAt(i - 1)||p.charAt(j-2)=='.') {
//匹配0个,比如aa和aaa*
if (dp[i][j - 2]) dp[i][j] = true;
//匹配一个,比如aaa和aaa*,也就是*可有可无
if (dp[i][j - 1]) dp[i][j] = true;
//匹配多个,比如aabbb和aab*,匹配多个任意个
if (dp[i - 1][j]) dp[i][j] = true;
}else if((dp[i][j - 2])){
//*以及它之前的那个字符不起作用,比如aa和aab*
dp[i][j] = true;
}
} else {
dp[i][j] = false;
}
}
}
return dp[slen][plen];
}
public int countAsterisk(String s) {
int len = s.length();
int count = 0;
for (int i = 0; i < len; i++) {
if (s.charAt(i) == '*') count++;
}
return count;
}
}
132. 分割回文串 II 困难
132. 分割回文串 II
使用动态规划,dp[i]表示s.substring(0,i)需要最少切割几次
class Solution {
public int minCut(String s) {
if(s == null || s.length() <= 1)
return 0;
int len = s.length();
int dp[] = new int[len];
Arrays.fill(dp, len-1);
for(int i = 0; i < len; i++){
findMinCut(s , i , i , dp); // 奇数回文串以1个字符为中心
findMinCut(s, i , i+1 , dp); // 偶数回文串以2个字符为中心
}
return dp[len-1];
}
private void findMinCut(String s, int i, int j, int[] dp){
int len = s.length();
while(i >= 0 && j < len && s.charAt(i) == s.charAt(j)){
//以当前字符为中心的最大回文串左侧为i,右侧为j,那s[i]~s[j]长度是不需要切割的
//只需要在s[i-1]处切一刀即可,即dp[i-1]+1。所以更新dp[j] = min(dp[j] , dp[i-1]+1)
dp[j] = Math.min(dp[j] , (i==0?-1:dp[i-1])+1);
i--;
j++;
}
}
}
91. 解码方法
class Solution {
int count=0;
public int numDecodings(String s) {
char[] arr=s.toCharArray();
if(arr[0]=='0'){
return 0;
}
int len=arr.length;
int[] dp=new int[len+1];
dp[0]=1;
dp[1]=1;
for(int i=1;i<len;i++){
int a=s.charAt(i)-'0';
int b=(s.charAt(i-1)-'0')*10+a;
if(a!=0) {
dp[i+1]+=dp[i];
}
if(b<=26&&b>=10) {
dp[i+1]+=dp[i-1];
}
}
return dp[len];
}
}

