参考Union-Find算法详解

  1. class UF {
  2.     // 连通分量个数
  3.     private int count;
  4.     // 存储一棵树
  5.     private int[] parent;
  6.     // 记录树的“重量”
  7.     private int[] size;
  9.     public UF(int n) {
  10.         this.count = n;
  11.         parent = new int[n];
  12.         size = new int[n];
  13.         for (int i = 0; i < n; i++) {
  14.             parent[i] = i;
  15.             size[i] = 1;
  16.         }
  17.     }
  19.     public void union(int p, int q) {
  20.         int rootP = find(p);
  21.         int rootQ = find(q);
  22.         if (rootP == rootQ)
  23.             return;
  25.         // 小树接到大树下面，较平衡
  26.         if (size[rootP] > size[rootQ]) {
  27.             parent[rootQ] = rootP;
  28.             size[rootP] += size[rootQ];
  29.         } else {
  30.             parent[rootP] = rootQ;
  31.             size[rootQ] += size[rootP];
  32.         }
  33.         count--;
  34.     }
  36.     public boolean connected(int p, int q) {
  37.         int rootP = find(p);
  38.         int rootQ = find(q);
  39.         return rootP == rootQ;
  40.     }
  42.     private int find(int x) {
  43.         //通过find来更新value值,进行路径压缩
  44.         if(x!=parent[x]){
  45.             int p = parent[x]
  46.             parent[x] = find(p);
  47.         }
  48.         return parent[x];
  49.     }
  51.     public int count() {
  52.         return count;
  53.     }
  54. }

被环绕的区域

[130]被围绕的区域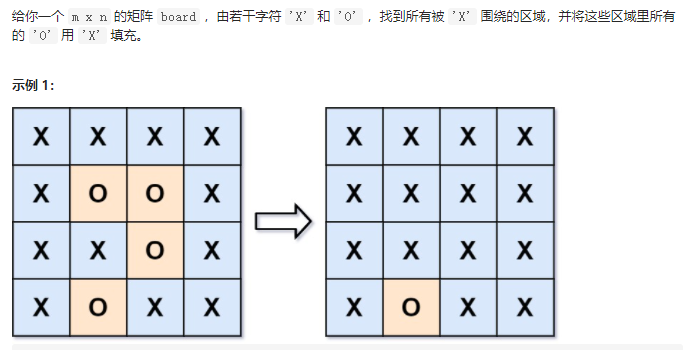
image.png
可以用dfs也可以用并查集

使用并查集

参数太多，什么xyij的混杂在一起，容易写错，使用dfs方法更清晰，效率也更高。
序列化二位矩阵[m,n] index=nx+y，index范围[0,mn-1]
给一个矩阵外的点dummy，dummy的index设置为m*n
首先把边界为’O’的点都与dummy相连接
再遍历非边界点，把值为’O’的点与周边为’O’的点相连
最后找到与dummy没有连接路径的点，标记为’X’

  1.   public void solve(char[][] board) {
  2.     int m = board.length;
  3.     if (m == 0) return;
  4.     int n = board[0].length;
  5.     UF uf = new UF(m * n + 1);
  6.     int dummy = m * n;
  7.     for (int i = 0; i < m; i++) {
  8.       if (board[i][0] == 'O') uf.union(dummy, n * i);
  9.       if (board[i][n - 1] == 'O') uf.union(dummy, n * i + n - 1);
  10.     }
  11.     for (int j = 0; j < n; j++) {
  12.       if (board[0][j] == 'O') uf.union(dummy, j);
  13.       if (board[m - 1][j] == 'O') uf.union(dummy, n * (m - 1) + j);
  14.     }
  15.     int[][] directions = new int[][]{{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
  16.     for (int i = 1; i < m - 1; i++) {
  17.       for (int j = 1; j < n - 1; j++) {
  18.         if (board[i][j] == 'O') {
  19.           for (int[] dir : directions) {
  20.             int x = i + dir[0];
  21.             int y = j + dir[1];
  22.             if (board[x][y] == 'O') uf.union(x * n + y, i * n + j);
  23.           }
  24.         }
  25.       }
  26.     }
  27.     for (int i = 1; i < m - 1; i++) {
  28.       for (int j = 1; j < n - 1; j++) {
  29.         if (!uf.connected(dummy, n * i + j)) board[i][j] = 'X';
  30.       }
  31.     }
  32.   }

使用dfs

找到边界为’O’的位置，并将与其相连的点都标记为’#’
那么余下的’O’就是被’X’包围的，最后循环的时候，把’O’改为’X’，把’#’改回’O’

  1. class Solution {
  2.   public void solve(char[][] board) {
  3.     int m = board.length;
  4.     if (m == 0) return;
  5.     int n = board[0].length;
  6.     for (int i = 0; i < m; i++) {
  7.       if (board[i][0] == 'O') dfs(i,0,board);
  8.       if (board[i][n - 1] == 'O') dfs(i,n-1,board);
  9.     }
  10.     for (int j = 0; j < n; j++) {
  11.       if (board[0][j] == 'O') dfs(0,j,board);
  12.       if (board[m - 1][j] == 'O') dfs(m-1,j,board);
  13.     }
  14.     for (int i = 0; i < m; i++) {
  15.       for (int j = 0; j < n; j++) {
  16.         if (board[i][j] == 'O') board[i][j]='X';
  17.         if (board[i][j] == '#') board[i][j]='O';
  18.       }
  19.     }
  20.   }
  22.   public void dfs(int x,int y,char[][] board){
  23.       if(board.length==0) return;
  24.       if(x<0||y<0||x>=board.length||y>=board[0].length||board[x][y]!='O') return;
  25.       board[x][y]='#';
  26.       dfs(x-1,y,board);
  27.       dfs(x+1,y,board);
  28.       dfs(x,y-1,board);
  29.       dfs(x,y+1,board);
  30.   }
  31. }

990. 等式方程的可满足性

[990]等式方程的可满足性
一个非常适合用并查集的例子

  1.   public boolean equationsPossible(String[] equations) {
  2.     int len = equations.length;
  3.     if (len == 0) return true;
  4.     UF uf = new UF(128);
  5.     for (String equation:equations) {
  6.       if (equation.charAt(1)=='!') continue;
  7.       char c1 = equation.charAt(0);
  8.       char c2 = equation.charAt(3);
  9.       uf.union(c1, c2);
  10.     }
  11.     for (String equation:equations) {
  12.       if (equation.charAt(1)=='=') continue;
  13.       char c1 = equation.charAt(0);
  14.       char c2 = equation.charAt(3);
  15.       if(uf.connected(c1,c2)) return false;
  16.     }
  17.     return true;
  18.   }

399. 除法求值

题目：399.除法求值
做了一个半小时，救命

  1. class Solution {
  2.     public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
  3.       Map<String,Integer> stringToIndex=new HashMap<>();
  4.       int k=0;
  5.       for(int i=0;i<equations.size();i++){
  6.         for(int j=0;j<2;j++){
  7.           String s=equations.get(i).get(j);
  8.           if(!stringToIndex.containsKey(s)){
  9.             stringToIndex.put(s,k++);
  10.           }
  11.         }
  12.       }
  13.       UnionFind uf=new UnionFind(k);
  14.       for(int i=0;i<equations.size();i++){
  15.         int i1=stringToIndex.get(equations.get(i).get(0));
  16.         int i2=stringToIndex.get(equations.get(i).get(1));
  17.         uf.union(i1,i2,values[i]);
  18.       }
  19.       int n=queries.size();
  20.       double[] res=new double[n];
  21.       for(int i=0;i<n;i++){
  22.         int i1=stringToIndex.getOrDefault(queries.get(i).get(0),-1);
  23.         int i2=stringToIndex.getOrDefault(queries.get(i).get(1),-1);
  24.         if(i1==-1||i2==-1) res[i]=-1.0;
  25.         else res[i]=uf.isConnected(i1,i2);
  26.       }
  27.       return res;
  28.     }
  30.     class UnionFind{
  31.       int[] parent;
  32.       double[] value;//index=i的节点到parent的值
  34.       public UnionFind(int n){
  35.         parent=new int[n];
  36.         value=new double[n];
  37.         for(int i=0;i<n;i++){
  38.           parent[i]=i;
  39.           value[i]=1.0;
  40.         }
  41.       }
  43.       public void union(int p,int q,double val){
  44.         //p/q=val
  45.         int rootp=find(p);
  46.         int rootq=find(q);
  47.         if(rootp==rootq) return;
  48.         parent[rootp]=rootq;
  49.         //注意这里
  50.         value[rootp]=val*value[q]/value[p];
  51.       }
  53.       public int find(int x){
  54.         //通过find来更新value值
  55.         if(x!=parent[x]){
  56.           //当还有parent的时候
  57.           int p=parent[x];
  58.           parent[x]=find(p);
  59.           value[x]=value[x]*value[p];
  60.         }
  61.         return parent[x];
  62.       }
  64.       public double isConnected(int p,int q){
  65.         int rootp=find(p);
  66.         int rootq=find(q);
  67.         if(rootp==rootq){
  68.           return value[p]/value[q];
  69.         }else{
  70.           return -1.0;
  71.         }
  72.       }
  73.     }
  74. }