判断链表是否有环

问题：

给定一个链表pHead，判断链表中是否存在环，如果存在，找出入环节点。

方法一：

哈希表，用一个 HashSet 保存已经访问过的节点，我们可以遍历整个列表并返回第一个出现重复的节点。
如果有环，则哈希表中已存在的节点就是入环节点。如果没环，不会有相同的节点。

• 时间复杂度O(n)
• 空间复杂度O(n)

代码：

public ListNode detectCycle(ListNode head) {
    HashSet<ListNode> visited = new HashSet<ListNode>();
    ListNode node = head;
    while (node != null) {
        if (visited.contains(node)) {
            return node;
        }
        visited.Add(node);
        node = node.next;
    }
    return null;
}

方法二(Floyd算法)：

快慢指针，pFast每次走两步，pSlow每次走一步。如果最终pFast == null 则不存在环。如果最终pFast == pSlow 则存在环。
如果存在环，则让pFast重新指向头结点，然后pFast和pSlow一起走（每次一步），则下次pFast == pSlow的时候，pFast和pSlow即为入环节点。

• 时间复杂度 O(n)
• 空间复杂度 O(1)

代码：

public ListNode DetectCycle(ListNode head) {
    if(head == null || head.next == null) {
        return null;
    }

    // pFast每次2步，pSlow每次1步
    ListNode pFast = head.next.next, pSlow = head.next;
    while (pFast != pSlow) {
        pSlow = pSlow.next;
        if(pFast != null) {
            pFast = pFast.next;
        }

        if(pFast != null) {
            pFast = pFast.next;
        }
    }

    // 如果pFast == null，说明到达链表结尾，不存在环，否则存在环，返回pFast即可
    // 判断是否存在环，到此即可
    if(pFast == null) {
        return null;
    }

    // pFast重新指向头结点
    pFast = head;
    // 两个指针同时走，相等时即为入环节点
    while (pFast != pSlow) {
        pSlow = pSlow.next;
        pFast = pFast.next;
    }

    return pFast;
}

方法二证明：

首先，在环中快指针肯定会追上慢指针。这样想，每走一步，两者之间距离会减少1，最终肯定会相遇。
利用这一点我们可以判断出是否存在环。
数学证明(链接)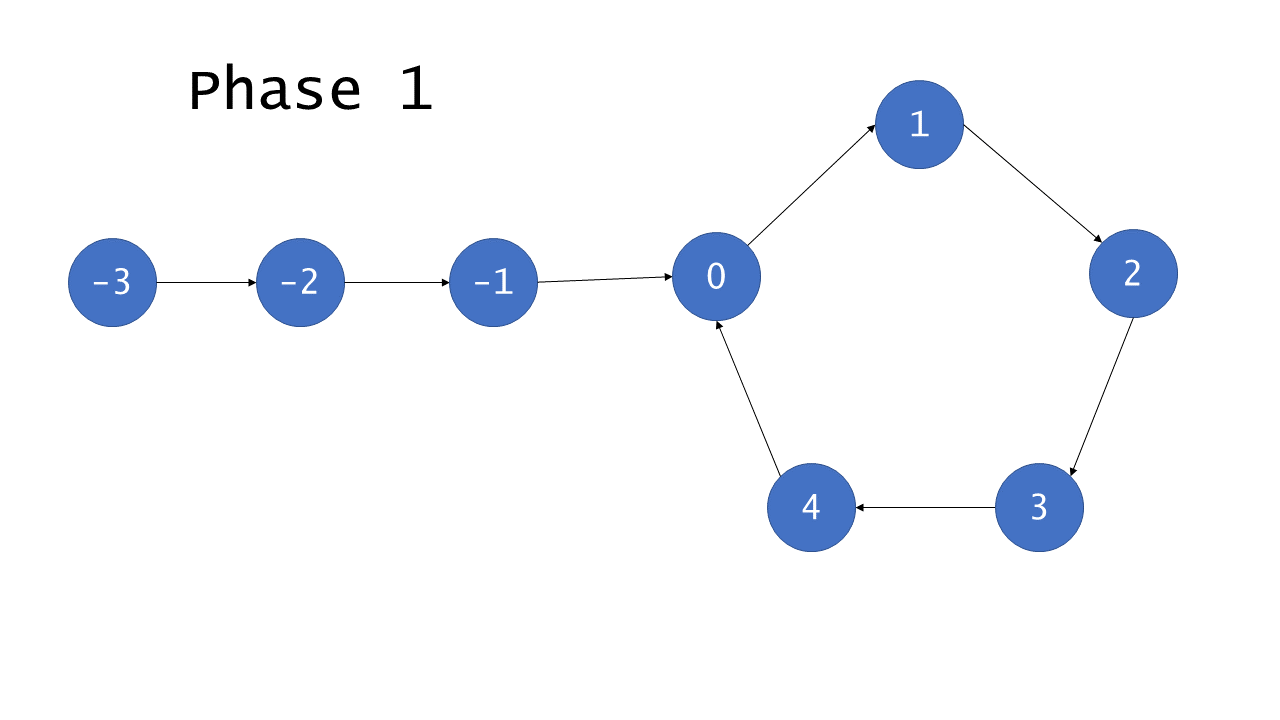

环中的节点从 0 到 C−1 编号，其中 C 是环的长度。非环节点从 −F 到 −1 编号，其中 F 是环以外节点的数目。 F 次迭代以后，慢指针指向了 0 且快指针指向某个节点 h ，其中 F≡h(modC) 。这是因为快指针在 F 次迭代中遍历了 2F 个节点，且恰好有 F 个在环中。继续迭代 C−h 次，慢指针显然指向第 C−h 号节点，而快指针也会指向相同的节点。原因在于，快指针从 h 号节点出发遍历了 2(C−h) 个节点。
h+2(C−h)=2C−h
≡C−h(modC)
因此，如果列表是有环的，快指针和慢指针最后会同时指向同一个节点，因此被称为 相遇 。

接下来，找入环节点。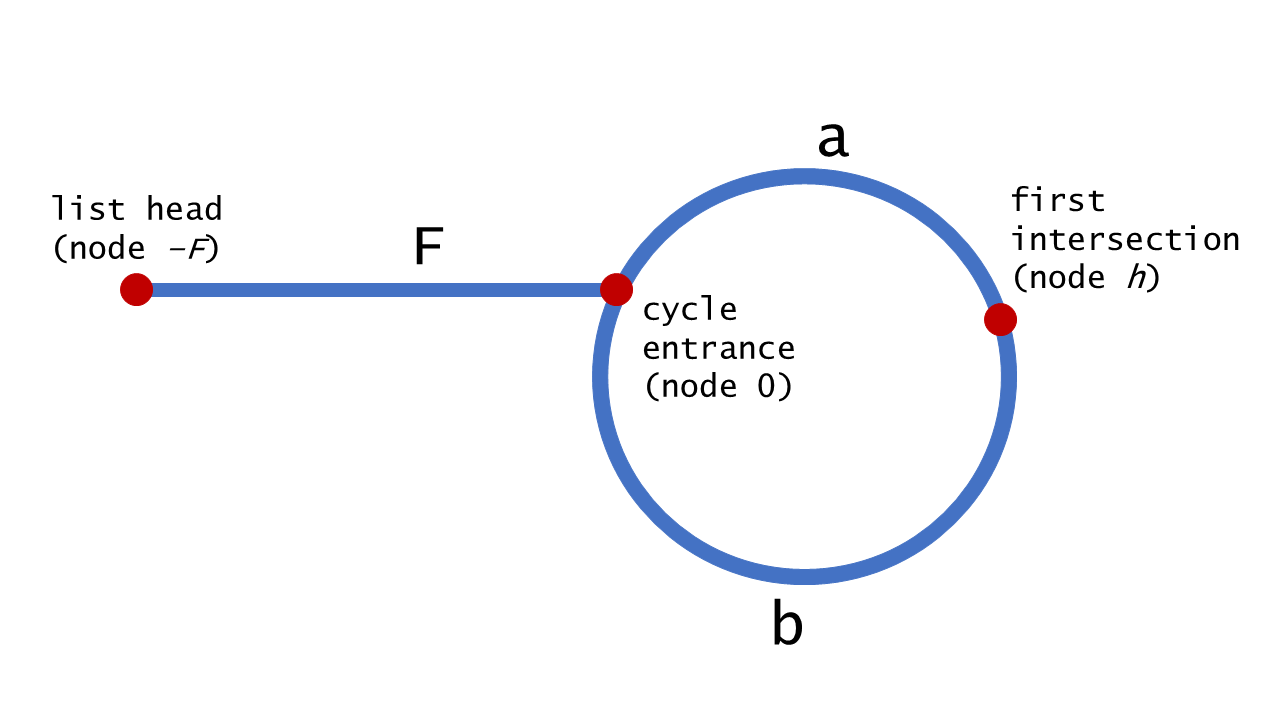

有如下等式：

2(F + a) = F + N(a + b) + a
 2F + 2a = F + 2a + b + (N - 1)(a + b)
       F = b + (N - 1)(a + b)

即pFast从头走了F步后，pSlow从相交节点开始走了(N-1)圈环后，又走了b步，到达入环节点。

例题：

141. 环形链表
142. 环形链表 II
202. 快乐数