二维前缀和

问题

给你一个 m * n 的矩阵 mat 和一个整数 K ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

• i - K <= r <= i + K, j - K <= c <= j + K
• (r, c) 在矩阵内。

  知识

  来源：Leetcode
  这题需要用到二维前缀和，二维前缀和是一维前缀和的拓展。
  设二维数组 A 的大小为 m * n，行下标的范围为 [1, m]，列下标的范围为 [1, n]。
  数组 P 是 A 的前缀和数组，等价于 P 中的每个元素 P[i][j]：
  如果 i 和 j 均大于 0，那么 P[i][j] 表示 A 中以 (1, 1) 为左上角，(i, j) 为右下角的矩形区域的元素之和；
  如果i 和 j 中至少有一个等于 0，那么 P[i][j] 也等于 0。
  数组 P 可以帮助我们在 的时间内求出任意一个矩形区域的元素之和。具体地，设我们需要求和的矩形区域的左上角为 (x1, y1)，右下角为 (x2, y2)，则该矩形区域的元素之和可以表示为：

sum = A[x1..x2][y1..y2]
   = P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]

以下图为例，当 A 的大小为 8 * 5，需要求和的矩形区域（深绿色部分）的左上角为 (3, 2)，右下角为 (5, 5) 时，该矩形区域的元素之和为P[5][5] - P[2][5] - P[5][1] + P[2][1]。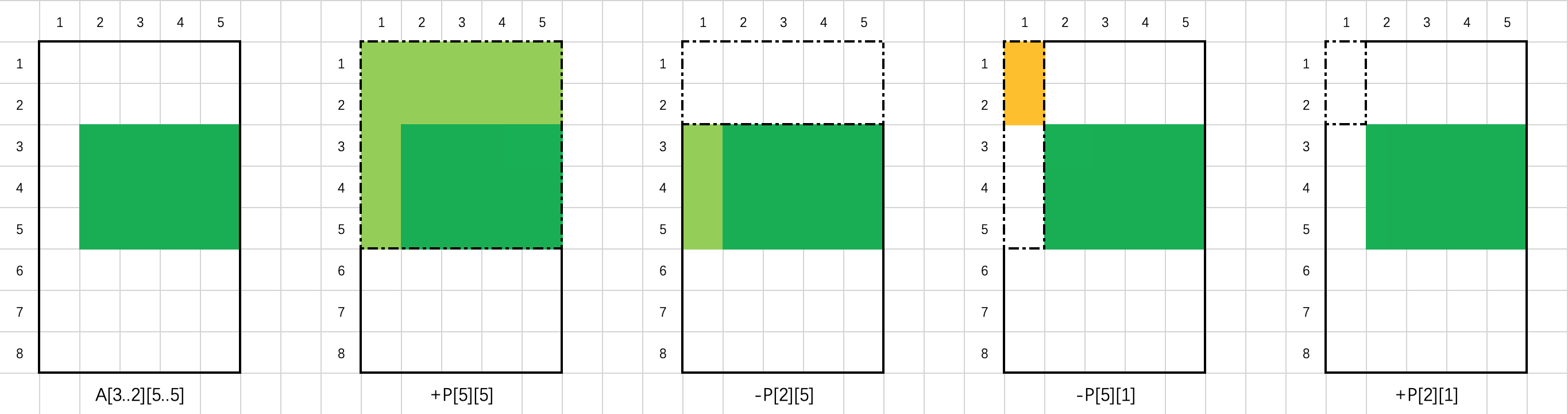

代码

use std::cmp::{max, min};
impl Solution {
    pub fn matrix_block_sum(mat: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        // 初始化矩阵前缀和
        let mut pm = vec![vec![0_i32;n + 1]; m + 1];
        for i in 1..=m{
            for j in 1..=n {
                pm[i][j] = mat[i-1][j-1] + pm[i-1][j] + pm[i][j-1] - pm[i-1][j-1];
            }
        }

        let mut ans = vec![vec![0_i32;n]; m];
        for i in 0..m {
            for j in 0..n{
                ans[i][j] = Solution::get_pm(&pm, i as i32 + k + 1, j as i32 + k + 1)
                        - Solution::get_pm(&pm, i as i32 - k, j as i32 + k + 1)
                        - Solution::get_pm(&pm, i as i32 + k + 1, j as i32 - k)
                        + Solution::get_pm(&pm, i as i32 - k, j as i32 - k);
  //pm[i + k + 1][j + k + 1] - pm[i - k][j + k + 1] - pm[i + k + 1][j - k] + pm[i - k][j - k];
            }
        }

        ans
    }

    pub fn get_pm(pm: &Vec<Vec<i32>>, i: i32, j: i32) -> i32 {
        // 边界判定
        let mut i = max(i, 0) as usize;
        let mut j = max(j, 0) as usize;
        i = min(i, pm.len() - 1);
        j = min(j, pm[0].len() - 1);
        pm[i][j]
    }
}

例题

1277. 统计全为 1 的正方形子矩阵