有限状态自动机拥有有限数量的状态，每个状态可以迁移到零个或多个状态，输入字串决定执行哪个状态的迁移。有限状态自动机可以表示为一个有向图。上过编译原理课就再熟悉不过了，可以用来做词法分析。

问题

验证给定的字符串是否可以解释为十进制数字。
存在于有效十进制数字中的字符列表：

  • 数字 0-9
  • 指数 -“e”
  • 正/负号 “+”/“-“
  • 小数点 “.”

示例：

  1. "0" => true
  2. " 0.1 " => true
  3. "abc" => false
  4. "1 a" => false
  5. "2e10" => true
  6. " -90e3   " => true
  7. " 1e" => false
  8. "e3" => false
  9. " 6e-1" => true
  10. " 99e2.5 " => false
  11. "53.5e93" => true
  12. " --6 " => false
  13. "-+3" => false
  14. "95a54e53" => false

思路

可以从开始一个部分一个部分的判断，正负号 -> 数字 - > . -> 数字 -> e -> 正负号 -> 数字，中间注意数字状态与非数字状态的判断就行。

也可以用自动机来做
可以画出状态转移图：
注：认为 .3 或 3. 也是正确的数字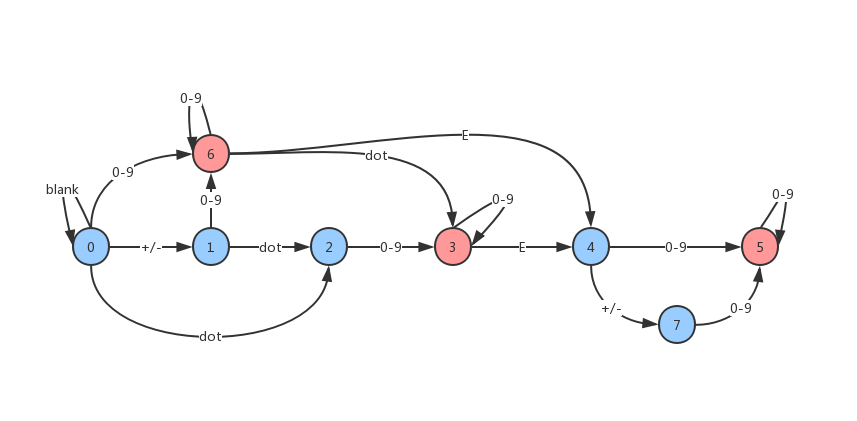
有限状态自动机(DFA) - 图1
状态转移可以用状态转移表表示：
这里不考虑首尾空格，可以减少一种状态
列首表示输入字符，行首表示当前状态，表格表示当前状态输入列首字符后转移到的状态。

状态\输入 ‘e’ ‘+’/‘-‘ ‘0’..’9’ ‘.’ other
0 start end signed number dot end
1 signed end end number dot end
2 dot end end float end end
3 float e end float end end
4 e end e_signed e_number end end
5 e_number end end e_number end end
6 number e end number float_dot end
7 e_signed end end e_number end end
end end end end end end

代码

pub struct Solution;

// 定义状态，起个名字，代码清晰些
#[derive(Hash, Eq, PartialEq, Copy, Clone)]
pub enum State {
    Start,
    Signed,
    Dot,
    Number,
    Float,
    E,
    ESigned,
    ENumber,
    End,
}

use std::collections::HashMap;
use State::*;

impl Solution {
    pub fn is_number(s: String) -> bool {
        // 写状态转移表，就是二维数组
        let mut state_table = HashMap::new();
        state_table.insert(Start,   vec![End, Signed, Number, Dot, End]);
        state_table.insert(Signed,  vec![End, End, Number, Dot, End]);
        state_table.insert(Dot,     vec![End, End, Float, End, End]);
        state_table.insert(Number,  vec![E, End, Number, Float, End]);
        state_table.insert(Float,   vec![E, End, Float, End, End]);
        state_table.insert(E,       vec![End, ESigned, ENumber, End, End]);
        state_table.insert(ESigned, vec![End, End, ENumber, End, End]);
        state_table.insert(ENumber, vec![End, End, ENumber, End, End]);
        // state_table.insert(End,     vec![End, End, End, End, End]);

        // 初始状态
        let mut state = Start;
        for c in s.trim().as_bytes() {
            // 获取输入对应的列
            let input_col = match c {
                b'e' => 0,
                b'+' | b'-' => 1,
                n if n.is_ascii_digit() => 2,
                b'.' => 3,
                _ => 4
            };

            // 进行状态转移
            state = state_table.get(&state).unwrap()[input_col];
            // 提前结束
            if state == End {
                return false;
            }
        }

        // 只有这三种状态才是正确的数字
        state == ENumber || state == Number || state == Float
    }
}