序

在 2018 年这个奇妙的秋天，我前往美国卡内基梅隆大学攻读硕士项目。为了准备实习秋招， 我从夏天就开始整理 LeetCode 的题目；经过几个月的刷题，我也整理了几百道题，但是缺少系统性的归纳和总结。时隔一年，我于 2019 年秋季在 GitHub 上用 Markdown 做了一个初步的总结， 按照算法和数据结构进行分类，整理了差不多 200 道题，用于自己在面试前查漏补缺。然而，在 这个简单的总结里，每道题只有简单的题目描述和题解代码，并没有详细的解释说明。除了我之外的其他人很难读懂代码的思路。
有了刷题的积累和不错的运气，我很快就在毕业前找到了工作。当时我的一位朋友对我开玩笑说，你刷了这么多题，却在找到工作后停止了面试，是不是有点亏啊。我笑了笑，心想我并不是会这么做的人；但是的确，刷了这么多题却没有派上太多用场。2019 年冬季毕业后，我宅在家里做着入职前的准备，同时刷着魔兽世界的坐骑成就。不知怎的，我突然萌生了一个念想，既然我刷了这么多题，也有了初步的总结，不如把它们好好地归纳总结一下，做一个便于他人阅读和学习的电子书。Bang! Here comes the book.
本书分为算法和数据结构两大部分，又细分了十五个章节，详细讲解了刷 LeetCode 时常用的技巧。我把题目精简到了 101 道，一是呼应了本书的标题，二是不想让读者阅读和练习时间过长。这么做不太好的一点是，如果只练习这 101 道题，读者可能对算法和数据结构的掌握不够扎实。因此在每一章节的末尾，我都加上了一些推荐的练习题，并给出了一些解法提示，希望读者在理解每一章节后把练习题也完成。如果本书反响热烈，我也会后续加上他们的题解。
本书以 C++ 作为编程语言。对于 Java 用户，绝大部分的算法和数据结构都可以找到对应的写法，语法上也只需要小修改。对于 Python 等其它用户，由于语法差别略大，这本书可能并不会特别适合你。由于本书的目的不是学习 C++ 语言，因此行文时我不会过多解释语法细节，而且会适当使用一些 C++11 或更新的语法。截止于 2019 年年末，所有的书内代码在 LeetCode 上都是可以正常运行的，并且在保持易读的基础上，几乎都是最快或最省空间的解法。
请注意，刷题只是提高面试乃至工作能力的一小部分。在计算机科学的海洋里，值得探索的东西太多，并不建议您花过多时间刷题。并且要成为一个优秀的计算机科学家，刷题只是入职的敲门砖，提高各种专业技能、打好专业基础、以及了解最新的专业方向或许更加重要。
由于本书的目的是分享和教学，因此本书永久免费，也禁止任何营利性利用。欢迎学术目的的分享和传阅。由于我不对 LeetCode 的任何题目拥有版权，一切题目版权以 LeetCode 官方为准。
感谢 GitHub 用户 CyC2018 的 LeetCode 题解，它对于我早期的整理起到了很大的帮助作用。 感谢 ElegantBook 提供的精美 LATEX 模版，使得我可以轻松地把 Markdown 笔记变成看起来更专业的电子书。另外，书的封面图片是我于 2019 年元月，在尼亚加拉大瀑布的加拿大侧拍摄的风景；在此感谢海澄兄同我一起旅行拍照。

第 1 章 题目分类

打开 LeetCode 网站，如果我们按照题目类型数量分类，最多的几个题型有数组、动态规划、 数学、字符串、树、哈希表、深度优先搜索、二分查找、贪心算法、广度优先搜索、双指针等等。 本书将包括上述题型以及网站上绝大多数流行的题型，并且按照难易程度和类型进行分类。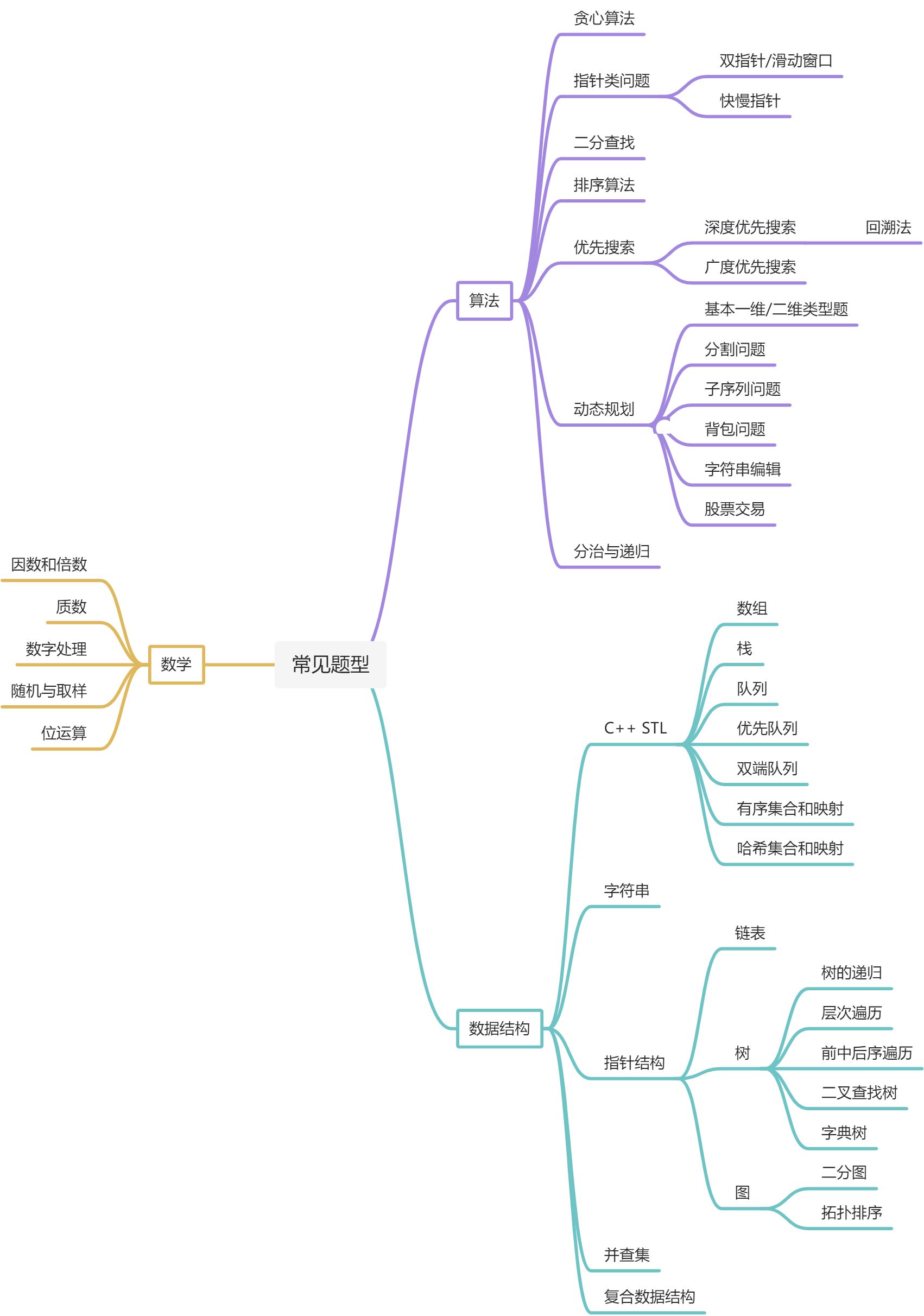

第一个大分类是算法。本书先从最简单的贪心算法讲起，然后逐渐进阶到二分查找、排序算 法和搜索算法，最后是难度比较高的动态规划和分治算法。
第二个大分类是数学，包括偏向纯数学的数学问题，和偏向计算机知识的位运算问题。这类问题通常用来测试你是否聪敏，在实际工作中并不常用，笔者建议可以优先把精力放在其它大类上。
第三个大分类是数据结构，包括 C++ STL 内包含的常见数据结构、字符串处理、链表、树和图。其中，链表、树、和图都是用指针表示的数据结构，且前者是后者的子集。最后我们也将介绍一些更加复杂的数据结构，比如经典的并查集和 LRU。

第 2 章 最易懂的贪心算法

2.1 算法解释

顾名思义，贪心算法或贪心思想采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。 举一个最简单的例子：小明和小王喜欢吃苹果，小明可以吃五个，小王可以吃三个。已知苹果园里有吃不完的苹果，求小明和小王一共最多吃多少个苹果。在这个例子中，我们可以选用的贪心策略为：每个人吃自己能吃的最多数量的苹果，这在每个人身上都是局部最优的。又因为全局结果是局部结果的简单求和，且局部结果互不相干，因此局部最优的策略也同样是全局最优的策略。

2.2 分配问题

455.Assign Cookies(Easy)

题目描述： :::tips 假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干j，都有一个尺寸s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。 ::: 示例1： :::info 输入：g = [1,2,3], s = [1,1]
输出：1
解释：你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。 ::: 示例2： :::info 输入：g = [1,2], s = [1,2,3]
输出：2
解释：你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2. ::: 提示：

• 1 <= g.length <= 3 * 104
• 0 <= s.length <= 3 * 104
• 1 <= g[i], s[j] <= 231 - 1

题解：

因为饥饿度最小的孩子最容易吃饱，所以我们先考虑这个孩子。为了尽量使得剩下的饼干可以满足饥饿度更大的孩子，所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。满足了这个孩子之后，我们采取同样的策略，考虑剩下孩子里饥饿度最小的孩子，直到没有满足条件的饼干存在。
简而言之，这里的贪心策略是，给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。 至于具体实现，因为我们需要获得大小关系，一个便捷的方法就是把孩子和饼干分别排序。 这样我们就可以从饥饿度最小的孩子和大小最小的饼干出发，计算有多少个对子可以满足条件。

注意： :::success

• 对数组或字符串排序是常见的操作，方便之后的大小比较。

• 在之后的讲解中，若我们谈论的是对连续空间的变量进行操作，我们并不会明确区分 数组 和 字符串 ，因为他们本质上都是在连续空间上的有序变量集合。一个字符串 "abc" 可以被看作一 个数组 ['a','b','c']。
  ::: 代码：

  class Solution {
  public:
   int findContentChildren(vector<int> &g, vector<int> &s) {
       sort(g.begin(), g.end());
       sort(s.begin(), s.end());
       int numOfChildren = g.size(), numOfCookies = s.size();
       int count = 0;
       for (int i = 0, j = 0; i < numOfChildren && j < numOfCookies; i++, j++) {
           while (j < numOfCookies && g[i] > s[j]) {
               j++;
           }
           if (j < numOfCookies) {
               count++;
           }
       }
       return count;
   }
  };

  func findContentChildren(g []int, s []int) int {
   //1.对数组 g s 进行排序,保证数组的有序性
   sort.Ints(g)
   sort.Ints(s)
   //2.初始化孩子和饼干数
   //child cookie 还代表着二者的index值(复用,避免多分配变量空间)
   child, cookie := 0, 0
   for child < len(g) && cookie < len(s) {
       //若能被喂饱 则二者index均往后走一位
       if g[child] <= s[cookie] {
           child++
           cookie++
       } else {
           //若当前饼干不足以喂饱最低饥饿度的孩子，则饼干索引值++
           cookie++
       }
   }
   return child
  }

  复杂度分析： :::warning

• 时间复杂度：，其中 m 和 n 分别是数组 g 和 s 的长度。对两个数组排序的时间复杂度是 ，遍历数组的时间复杂度是 ，因此总时间复杂度是。

• 空间复杂度：，其中 m 和 n 分别是数组 g 和 s 的长度。空间复杂度主要是排序的额外空间开销。 :::

  135.Candy(Hard)

  题目描述： :::tips n 个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。
  你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。

• 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。 ::: 示例1： :::info 输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。 ::: 示例2： :::info 输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。 ::: 提示：

• n == ratings.length
• 1 <= n <= 2 * 104
• 0 <= ratings[i] <= 2 * 104

题解：
解法一：两次遍历

做完了题目 455，你会不会认为存在比较关系的贪心策略一定需要排序或是选择？虽然这一道题也是运用贪心策略，但我们只需要简单的两次遍历即可：把所有孩子的糖果数初始化为 1； 先从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的 糖果数加 1；再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数 不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果数加 1。通过这两次遍历， 分配的糖果就可以满足题目要求了。这里的贪心策略即为，在每次遍历中，只考虑并更新相邻一 侧的大小关系。 在样例中，我们初始化糖果分配为 [1,1,1]，第一次遍历更新后的结果为 [1,1,2]，第二次遍历更新后的结果为 [2,1,2]。

解法二：常数空间遍历

没理解，下次再看……

代码：
解法一：两次遍历

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n = ratings.size();
        vector<int> left(n);
        for (int i = 0; i < n; i++) {
            if (i > 0 && ratings[i] > ratings[i - 1]) {
                left[i] = left[i - 1] + 1;
            } else {
                left[i] = 1;
            }
        }
        int right = 0, ret = 0;
        for (int i = n - 1; i >= 0; i--) {
            if (i < n - 1 && ratings[i] > ratings[i + 1]) {
                right++;
            } else {
                right = 1;
            }
            ret += max(left[i], right);
        }
        return ret;
    }
};

func candy(ratings []int) (ans int) {
    n := len(ratings)
    //000 - 100 - 110 - 112
    left := make([]int, n)
    for i, r := range ratings {
        if i > 0 && r > ratings[i-1] {
            left[i] = left[i-1] + 1
        } else {
            left[i] = 1
        }
    }
    //1-1-2
    right := 0
    for i := n - 1; i >= 0; i-- {
        if i < n-1 && ratings[i] > ratings[i+1] {
            right++
        } else {
            right = 1
        }
        //比较左右两个遍历的数组中,哪个值相对来说更大,更大的值存入到ans中
        ans += max(left[i], right)
    }
    return
}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

复杂度分析： :::warning

• 时间复杂度：，其中 n 是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。

• 空间复杂度：，其中 n 是孩子的数量。我们需要保存所有的左规则对应的糖果数量。 ::: 解法二：常数空间遍历

  class Solution {
    public:
    int candy(vector<int>& ratings) {
        int n = ratings.size();
        int ret = 1;
        int inc = 1, dec = 0, pre = 1;
        for (int i = 1; i < n; i++) {
            if (ratings[i] >= ratings[i - 1]) {
                dec = 0;
                pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;
                ret += pre;
                inc = pre;
            } else {
                dec++;
                if (dec == inc) {
                    dec++;
                }
                ret += dec;
                pre = 1;
            }
        }
        return ret;
    }
  };

  func candy(ratings []int) int {
    n := len(ratings)
    ans, inc, dec, pre := 1, 1, 0, 1
    for i := 1; i < n; i++ {
        if ratings[i] >= ratings[i-1] {
            dec = 0
            if ratings[i] == ratings[i-1] {
                pre = 1
            } else {
                pre++
            }
            ans += pre
            inc = pre
        } else {
            dec++
            if dec == inc {
                dec++
            }
            ans += dec
            pre = 1
        }
    }
    return ans
  }

  复杂度分析： :::warning

• 时间复杂度：，其中 n 是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。

• 空间复杂度：。我们只需要常数的空间保存若干变量。 :::

2.3 区间问题

435.Non-overlapping Intervals(Medium)

题目描述： :::tips 给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。 ::: 示例1： :::info 输入：intervals = [[1,2],[2,3],[3,4],[1,3]]
输出：1
解释：移除 [1,3] 后，剩下的区间没有重叠。 ::: 示例2： :::info 输入：intervals = [ [1,2], [1,2], [1,2] ]
输出：2
解释：你需要移除两个 [1,2] 来使剩下的区间没有重叠。 ::: 示例3： :::info 输入：intervals = [ [1,2], [2,3] ]
输出：0
解释：你不需要移除任何区间，因为它们已经是无重叠的了。 ::: 提示：

• 1 <= intervals.length <= 105
• intervals[i].length == 2
• -5 * 104 <= starti < endi <= 5 * 104

题解：

在选择要保留区间时，区间的结尾十分重要：选择的区间结尾越小，余留给其它区间的空间就越大，就越能保留更多的区间。因此，我们采取的贪心策略为，优先保留结尾小且不相交的区间。 具体实现方法为，先把区间按照结尾的大小进行增序排序，每次选择结尾最小且和前一个选择的区间不重叠的区间。我们这里使用 C++ 的 Lambda，结合 std::sort() 函数进行自定义排 序。 在样例中，排序后的数组为 [[1,2], [1,3], [2,4]]。按照我们的贪心策略，首先初始化为区间 [1,2]；由于 [1,3] 与 [1,2] 相交，我们跳过该区间；由于 [2,4] 与 [1,2] 不相交，我们将其保留。因此最终保留的区间为 [[1,2], [2,4]]。

注意： :::success 需要根据实际情况判断按区间开头排序还是按区间结尾排序。
::: 代码：
解法一：动态规划

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.empty()) {
            return 0;
        }
        sort(intervals.begin(), intervals.end(), [](const auto& u, const auto& v) {
            return u[0] < v[0];
        });
        int n = intervals.size();
        vector<int> f(n, 1);
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (intervals[j][1] <= intervals[i][0]) {
                    f[i] = max(f[i], f[j] + 1);
                }
            }
        }
        return n - *max_element(f.begin(), f.end());
    }
};

func eraseOverlapIntervals(intervals [][]int) int {
    n := len(intervals)
    if n == 0 {
        return 0
    }
    sort.Slice(intervals, func(i, j int) bool { return intervals[i][0] < intervals[j][0] })
    dp := make([]int, n)
    for i := range dp {
        dp[i] = 1
    }
    for i := 1; i < n; i++ {
        for j := 0; j < i; j++ {
            if intervals[j][1] <= intervals[i][0] {
                dp[i] = max(dp[i], dp[j]+1)
            }
        }
    }
    return n - max(dp...)
}
func max(a ...int) int {
    res := a[0]
    for _, v := range a[1:] {
        if v > res {
            res = v
        }
    }
    return res
}

复杂度分析： :::warning

• 时间复杂度：，其中 n 是区间的数量。我们需要 的时间对所有的区间按照左端点进行升序排序，并且需要 的时间进行动态规划。由于前者在渐进意义下小于后者，因此总时间复杂度为 。注意到方法一本质上是一个「最长上升子序列」问题，因此我们可以将时间复杂度优化至 ，具体可以参考「300. 最长递增子序列的官方题解」。

• 空间复杂度：，即为存储所有状态 fi需要的空间。 ::: 解法二：贪心

  class Solution {
  public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.empty()) {
            return 0;
        }
        sort(intervals.begin(), intervals.end(), [](const auto& u, const auto& v) {
            return u[1] < v[1];
        });
        int n = intervals.size();
        int right = intervals[0][1];
        int ans = 1;
        for (int i = 1; i < n; ++i) {
            if (intervals[i][0] >= right) {
                ++ans;
                right = intervals[i][1];
            }
        }
        return n - ans;
    }
  };

  func eraseOverlapIntervals(intervals [][]int) int {
    //保留最小区间且不相交重叠的
    //1.先把区间按结尾大小进行升序排序，每次选择结尾最小且和前一个选择的区间不重叠的区间。
    size := len(intervals)
    //1.判空
    if size <= 1 {
        return 0
    }
    //2.利用sort包的Slice(SliceStable速度会慢上一倍左右)将intervals[][]int中的items的结尾进行排序
    //小的放在前面，大的放在后面。由于intervals[]int内部size为2,则tail的index=1
    sort.Slice(intervals, func(i, j int) bool { return intervals[i][1] < intervals[j][1] })
    //3.此时数组已经排序完成,初始化要移除的区间数量total 和前一个intervals[]中的tail元素
    total, tail := 0, intervals[0][1]
    //4.循环遍历数组切片区间,比较后一个元素的prev值和前一个元素的tail值。
    //若prev < tail,则说明有重叠区间,total++
    for i := 1; i < size; i++ {
        if intervals[i][0] < tail {
            total++
        } else {
            tail = intervals[i][1]
        }
    }
    return total
  }

  复杂度分析： :::warning

• 时间复杂度：，其中 n 是区间的数量。我们需要 的时间对所有的区间按照右端点进行升序排序，并且需要 的时间进行遍历。由于前者在渐进意义下大于后者，因此总时间复杂度为 。

• 空间复杂度：，即为排序需要使用的栈空间。 :::

2.4 练习

基础难度

605.Can Place Flowers(Easy)

Q：采取什么样的贪心策略，可以种植最多的花朵呢？ A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

452.Minimum Number of Arrows to Burst Balloons(Medium)

Q：这道题和题目 435 十分类似，但是稍有不同，具体是哪里不同呢？
A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

763.Partition Labels (Medium)

Q： 为了满足你的贪心策略，是否需要一些预处理？
A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

122.Best Time to Buy and Sell Stock II (Easy)

Q：股票交易题型里比较简单的题目，在不限制交易次数的情况下，怎样可以获得最大利润呢？
A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

406.Queue Reconstruction by Height (Medium)

Q：温馨提示，这道题可能同时需要排序和插入操作。
A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

665.Non-decreasing Array (Easy)

Q：需要仔细思考你的贪心策略在各种情况下，是否仍然是最优解。
A：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

第 3 章 玩转双指针

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

第 4 章 居合斩！二分查找

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

第 5 章 千奇百怪的排序算法

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

第 6 章 一切皆可搜索

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
复杂度分析： :::warning

::: 解法二：
复杂度分析： :::warning

::: 解法三：
复杂度分析： :::warning

:::

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
解法二：
解法三：

第 7 章 深入浅出动态规划

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
解法二：
解法三：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
解法二：
解法三：

第 8 章 化繁为简的分治法

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
解法二：
解法三：

题目描述： :::tips

::: 示例1： :::info

::: 示例2： :::info

::: 示例3： :::info

::: 提示：

题解： :::success
::: 代码：
解法一：
解法二：
解法三：

第 9 章 巧解数学问题

第 10 章 神奇的位运算

第 11 章 妙用数据结构

第 12 章 令人头大的字符串

第 13 章 指针三剑客之一：链表

第 14 章 指针三剑客之二：树

第 15 章 指针三剑客之一：图

第 16 章 更加复杂的数据结构