1、基本思想

1.1、递归遍历

模板： :::tips 1、确定函数的返回值
2、确定终止条件
3、确定单层递归的逻辑 :::

1.2、迭代法实现遍历

基本思想：使用栈来模拟递归

1.2.1、前序遍历

  • 手动模拟 :::tips 利用栈先进后出的特性，右左中节点以此入栈 :::

  • 代码 ```java class Solution { public List preorderTraversal(TreeNode root) {

    1.   List<Integer> result = new ArrayList<>();
    2.   if (root == null){
    3.       return result;
    4.   }
    5.   Stack<TreeNode> stack = new Stack<>();
    6.   stack.push(root); //根节点入栈
    7.   while (!stack.isEmpty()){
    8.       TreeNode node = stack.pop(); //出栈
    9.       result.add(node.val);
    10.       if (node.right != null){
    11.           stack.push(node.right);//右节点入栈
    12.       }
    13.       if (node.left != null){
    14.           stack.push(node.left); //左节点入栈
    15.       }
    16.   }
    17.   return result; //返回节点

    } }

  2. <a name="Ik60o"></a>
  3. ### 1.2.2、后序遍历
  5. - 思想
  6. :::tips
  7. 基本思想与前序一致，调整左右节点的入栈顺序，最后在反转数组<br />中左右-->中右左-->左右中
  8. :::
  10. - 代码
  11. ```java
  12. class Solution {
  13.     public List<Integer> postorderTraversal(TreeNode root) {
  14.         List<Integer> result = new ArrayList<>();
  15.         if (root == null){
  16.             return result;
  17.         }
  18.         Stack<TreeNode> stack = new Stack<>();
  19.         stack.push(root);
  20.         while (!stack.isEmpty()){
  21.             TreeNode node = stack.pop();
  22.             result.add(node.val);
  23.             if (node.left != null){ //左节点
  24.                 stack.push(node.left);
  25.             }
  26.             if (node.right != null){ //右节点
  27.                 stack.push(node.right);
  28.             }
  29.         }
  30.         Collections.reverse(result); //数组反转
  31.         return result;
  32.     }
  33. }

1.2.3、中序遍历

  • 思想 :::tips 根节点入栈，如果左子树不为空，则持续将左子树加入栈中
    左子树为空时，将节点出栈，并记录到结果数组中，然后访问右节点 :::

  • 代码

    1.   public List<Integer> inorderTraversal(TreeNode root) {
    2.       ArrayList<Integer> integers = new ArrayList<>();
    3.       if (root==null) return integers;
    4.       Stack<TreeNode> stack = new Stack<>();
    5.       TreeNode node = root; //与其他两种方式不同，这里无需进行初始化
    6.       while (node!=null || !stack.isEmpty()){
    7.           if (node!=null){
    8.               stack.push(node);
    9.               node=node.left;
    10.           }else {
    11.               node= stack.pop();//无左子树，出栈，并加入结果中
    12.               integers.add(node.val);
    13.               node=node.right; //
    14.           }
    15.       }return integers;
    16.   }

1.3、层次遍历

  • 思想 :::tips 利用队列先进先出的特点
    从根节点开始入队，获取当前队列大小，每次只访问当前层的节点，将当前节点加入对应结果的数组中，然后将子节点入队，供下一层重复当前操作，直至队列为空时返回结果。 :::

  • 代码

    1. public List<List<Integer>> levelOrder(TreeNode root) {
    2.       ArrayList<List<Integer>> lists = new ArrayList<>();
    3.       if (root==null) return lists;
    4.       Queue<TreeNode> queue = new LinkedList<TreeNode>(); //LinkList实现的一个队列
    5.       queue.offer(root);
    6.       while (!queue.isEmpty()){
    7.           ArrayList<Integer> level = new ArrayList<Integer>(); //当前层的结果
    8.           int size= queue.size(); //从根节点开始，利用队列先进先出的特点，每次访问当前层的节点，并将其对应子节点加入到队列中供下次访问。
    9.           System.out.println("队列大小"+size);
    10.           for (int i = 0; i < size; i++) {
    11.               TreeNode node = queue.poll();
    12.               level.add(node.val);
    13.               if (node.left!=null) queue.add(node.left);
    14.               if (node.right!=null) queue.add(node.right);
    15.           }
    16.           lists.add(level);
    17.       }
    18.       return lists;
    19. }

    1.4、反转二叉树

    思路简单，只需要在递归、迭代和层次的基础上加上swap就行

  • DFS

    1.   public TreeNode invertTree(TreeNode root) {
    2.       TreeNode head = root;
    3.       if (root==null) return root;
    4.       swap(root);
    5.       invertTree(root.left);
    6.       invertTree(root.right);
    7.       return root;
    8.   }

  • BFS

    1. public TreeNode invertTreeBFS(TreeNode root){
    2.       TreeNode head = root;
    3.       if (head==null) return root;
    4.       Queue<TreeNode> queue =new LinkedList<>();
    5.       queue.offer(root);
    6.       while (!queue.isEmpty()){
    8.           int size = queue.size();
    9.           for (int i = 0; i < size; i++) {
    10.               TreeNode node =queue.poll();
    11.               swap(node);
    12.               if (node.left!=null) queue.offer(node.left);
    13.               if (node.right!=null) queue.offer(node.right);
    14.           }
    15.       }
    16.       return head;
    17.   }

  • 迭代

    1. public TreeNode inver(TreeNode root){
    2.       TreeNode head = root;
    3.       if (root==null) return root;
    4.       Stack<TreeNode> treeNodes = new Stack<>();
    5.       treeNodes.push(root);
    6.       while (!treeNodes.isEmpty()){
    7.           TreeNode node = treeNodes.pop();
    8.           swap(node);
    9.           if (node.left!=null) treeNodes.push(node.left);
    10.           if (node.right!=null) treeNodes.push(node.right);
    11.       }
    12.       return head;
    13.   }

1.4、对称二叉树

二叉树是否对称，需要将左右的外侧与外侧比，内侧与内侧比

  1. 递归

    递归函数是布尔值，终止条件是如果左右子树不相等则返回false，左子树右子树都为空时返回true，左右子树相等时，用外侧与内侧同时递归，在内外都为true时，才返回true，并返回上一层递归，以此类推。

  1.     public boolean isSymmetric(TreeNode root) {
  2.         if (root==null) return false;
  3.         return conpare(root.left,root.right);
  4.     }
  6.       boolean conpare(TreeNode left,TreeNode right){
  7.           //当左右节点不同时为空时，返回f
  8.         if (left==null&&right!=null || left!=null&&right==null) return false;
  9.             //当左右节点都为空时，返回t
  10.         else if (left==null&&right==null) return true;//返回条件
  11.             //当不为空，且左右节点不一致
  12.         else if (left.val!=right.val) return false;
  13.             //剩下一种可能，当左右节点不为空且值不一致时
  14.         else  {
  15.             boolean out = conpare(left.left,right.right); //子树的外侧
  16.             boolean inner = conpare(left.right,right.left); //子树的内测
  17.             return out&&inner; //只有内外全部一致的时候才能返回true
  18.         }
  1. 迭代

    迭代思路简单，可以使用队列或者栈作为工具进行判断，此处以队列为例 主要思路还是左右的内侧与外侧同时入队，来比较左右的大小

  1.   public boolean isSymmetric(TreeNode root) {
  2.         if (root==null) return false;
  3.         Queue<TreeNode> queue = new LinkedList<>();
  4.         //将根节点的左右子树入队
  5.         queue.offer(root.left);
  6.         queue.offer(root.right);
  7.         while (!queue.isEmpty()){
  8.             //两个数据出队
  9.             TreeNode left = queue.poll();
  10.             TreeNode right = queue.poll();
  11.             if (left==null&&right==null) continue;
  12.             else if (right==null || left==null || right.val!=left.val) return false;
  13.             //外侧入队
  14.             queue.offer(left.left);
  15.             queue.offer(right.right);
  16.             //内侧入队
  17.             queue.offer(left.right);
  18.             queue.offer(right.left);
  19.         }
  20.         return true;
  21.     }

迭代只是一种思想，且并非只有栈一种处理方式

1.5、二叉树的最大深度

前序求的就是深度，使用后序求的是高度。

  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

1.5.1、递归法

  1. 后序遍历

    1.  public int maxDepth(TreeNode root) {
    2.      //从底部开始算，因此本质上是求其深度，深度和高度相等
    3.   if (root==null) return 0; //叶子节点高度为1
    4.   return Math.max(maxDepth(root.left),maxDepth(root.right))+1; //简略的后序遍历
    5.  }

  2. 前序遍历

    1.  int result;
    2.  public int maxDepth(TreeNode root) {
    3.      result=0;
    4.      if(root==null) return 0;
    5.      getDeepth (root,1); //根节点深度为1
    6.      return result;
    8.  }
    9.  void getDeepth (TreeNode node,int deepth){
    10.      result = Math.max(result,deepth); //前序遍历
    11.      // System.out.println(String.valueOf(node.val)+"对应深度："+deepth);
    12.      if(node.left==null&&node.right==null) return; //递归必有返回条件
    14.      if (node.left!=null){ //左
    15.          getDeepth(node.left,++deepth);
    16.          deepth--;
    17.      }
    18.      if (node.right!=null){
    19.          getDeepth(node.right,++deepth);
    20.          deepth--;
    21.      }
    22.      return;
    23.  }

1.5.2、迭代

使用层次遍历，每层deepth + 1，代码省略

1.6、二叉树的最小深度

求深度问题，默认使用后序排序 由于最小深度是对于头节点到叶子节点的距离，所以需要排除左右节点为空的情况

  1.     public int minDepth(TreeNode root) {
  2.         if (root==null) return 0;
  3.         int lefth=minDepth(root.left);
  4.         int righth=minDepth(root.right);
  5.         //题目是根节点到叶子节点的最小距离
  6.         //所以需要排除掉左右子树分别为空的情况
  7.         if (root.left!=null&&root.right==null) return 1+lefth;
  8.         if (root.right!=null&&root.left==null) return 1+righth;
  9.         return 1+Math.min(lefth,righth);
  10.     }

1.6、二叉树的所有路径

求路径需要用后续遍历 此题可分为两种情况：

  1. 一般二叉树的求解
  2. 完全二叉树的求解
  1. 一般二叉树： ```java // 通用递归解法 public int countNodes(TreeNode root) {
    1.  if(root == null) {
    2.      return 0;
    3.  }
    4.  return countNodes(root.left) + countNodes(root.right) + 1;
    }
  2. 2. 完全二叉树
  3. ```java
  4.     public int countNodes(TreeNode root) {
  5.         if(root==null) return 0; //出递归条件
  6.         //取出左右节点
  7.         TreeNode left = root.left;
  8.         TreeNode right = root.right;
  9.         //定义左右节点的长度
  10.         int leftl=0,rightl=0;
  11.         //遍历左节点
  12.         while (left!=null){
  13.             left=left.left;
  14.             leftl++;
  15.         }
  16.         while (right!=null){
  17.             right=right.right;
  18.             rightl++;
  19.         }
  20.         //如果左右节点长度一致，则说明该子树为满二叉树，用满二叉树的计算公式
  21.         if (rightl==leftl) return (2<<leftl)-1;
  22.         //如果左右节点不一致，则递归访问左右节点长度，然后加1 （子树根节点）
  23.         return countNodes(root.left)+countNodes(root.right)+1;
  24.     }

补充：

1.7、左叶子之和

由于是左叶子，因此不能简单的用层次遍历取最左边的节点 可以使用DFS 前序遍历 本题使用迭代的方式

  1.     public int sumOfLeftLeaves(TreeNode root) {
  2.         if(root==null) return 0;
  3.         Stack<TreeNode> stack = new Stack<>();
  4.         stack.push(root);
  5.         int res =0 ;
  6.         //用栈使用迭代遍历进行前序遍历
  7.         while (!stack.isEmpty()){
  8.             TreeNode node = stack.pop();
  9.             //左叶子树的遍历条件
  10.             if (node.left!=null&&node.left.left==null&&node.left.right==null){
  11.                 res+=node.left.val;
  12.             }
  13.             if (node.left!=null) stack.push(node.left);
  14.             if (node.right!=null) stack.push(node.right);
  15.         }
  16.         return res;
  17.     }

1.8、路径之和

  1.     public boolean hasPathSum(TreeNode root, int targetSum) {
  2.         if (root==null) return false;
  3.         return getSum(root,targetSum);
  5.     }
  7.     //定义的递归函数，返回值是Boolean
  8.     boolean getSum(TreeNode node,int tar){
  9.         // System.out.println("当前节点："+ node.val+"当前tar: "+tar);
  10.         //如果叶节点，且路径之和和目标值相等，则返回true
  11.         if (node.left==null && node.right==null && tar==node.val) return true;
  12.         if (node.left==null &&node.right==null) return false;
  13.         if (node.left!=null){
  14.             //子树正确，也直接返回
  15.             if(getSum(node.left,tar-node.val)) return true;
  16.         }
  17.         if (node.right!=null){
  18.             //子树正确，也直接返回
  19.             if (getSum(node.right,tar-node.val)) return true;
  20.         }
  21.         //如果不符合上面的条件，则返回f
  22.         return false;
  23.     }

1.9、中序遍历与后续遍历序列构造二叉树

树的还原过程：

  • 首先在后序遍历序列中找到根节点(最后一个元素)
  • 根据根节点在中序遍历序列中找到根节点的位置
  • 根据根节点的位置将中序遍历序列分为左子树和右子树
  • 根据根节点的位置确定左子树和右子树在中序数组和后续数组中的左右边界位置
  • 递归构造左子树和右子树
  • 返回根节点结束

用到的变量：

  • HashMap memo 需要一个哈希表来保存中序遍历序列中,元素和索引的位置关系.因为从后序序列中拿到根节点后，要在中序序列中查找对应的位置,从而将数组分为左子树和右子树
  • int ri 根节点在中序遍历数组中的索引位置
  • 中序遍历数组的两个位置标记 [is, ie]，is 是起始位置，ie 是结束位置
  • 后序遍历数组的两个位置标记 [ps, pe] ps 是起始位置，pe 是结束位置

    位置关系的计算

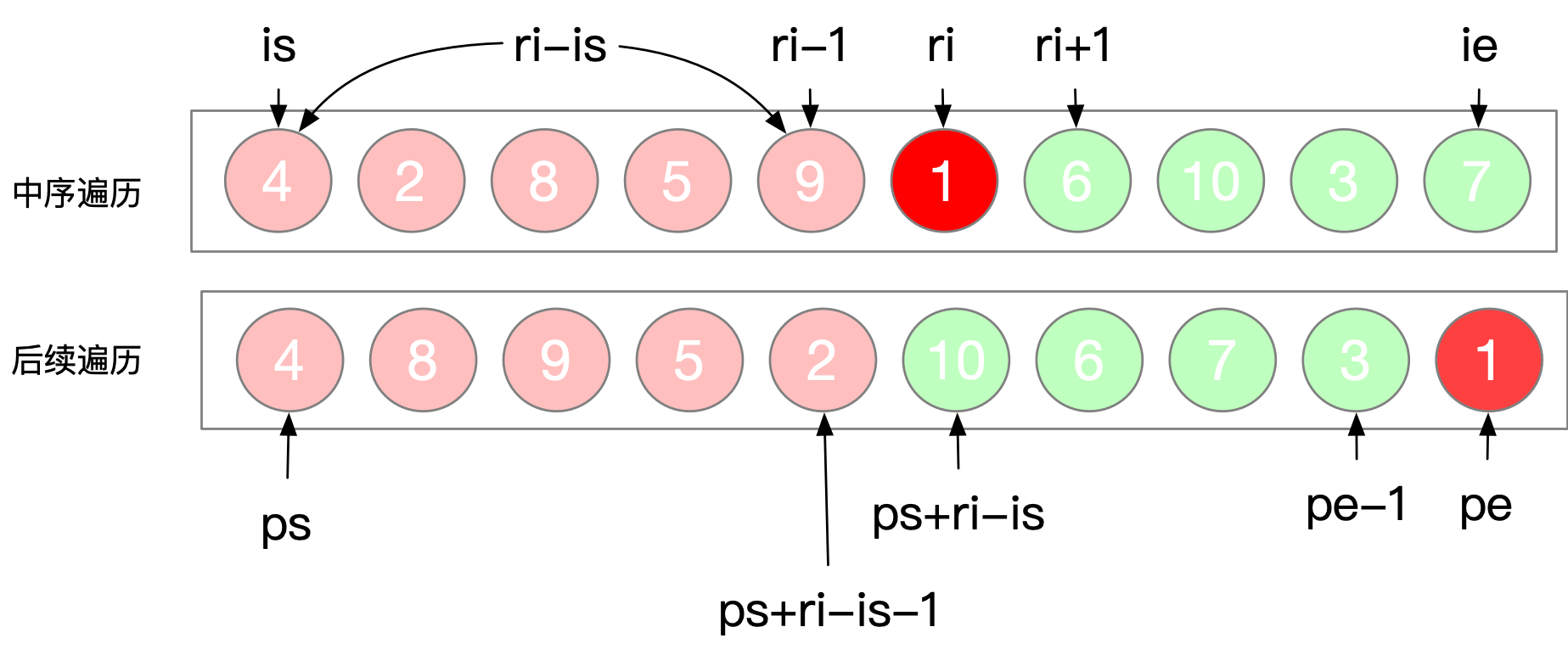
    左子树-中序数组 is = is, ie = ri - 1 左子树-后序数组 ps = ps, pe = ps + ri - is - 1 (pe计算过程解释，后续数组的起始位置加上左子树长度-1 就是后后序数组结束位置了，左子树的长度 = 根节点索引-左子树) 右子树-中序数组 is = ri + 1, ie = ie 右子树-后序数组 ps = ps + ri - is, pe - 1 image.png
  1. class Solution {
  2.       //map辅助空间，存储中序值-位置的映射
  3.     HashMap<Integer, Integer> map = new HashMap<>();
  4.     //记录后序遍历数组
  5.     int[] post;
  6.     public TreeNode buildTree(int[] inorder, int[] postorder) {
  7.         for (int i = 0; i < inorder.length; i++) {
  8.             map.put(inorder[i], i);
  9.         }
  10.         //存入后序辅助数组
  11.         post=postorder;
  12.         return buildTree(0, inorder.length - 1, 0, postorder.length - 1);
  13.     }
  15.     //is:前序始节点，ie:前序终结点，ps:后序始节点，pe：后序终结点
  16.     TreeNode buildTree(int is,int ie,int ps,int pe) {
  17.         //递归函数的终止条件
  18.         if (is>ie || ps>pe) return null;
  19.         //由后序遍历性质，得到子树的头节点
  20.         int root = post[pe];
  21.         //在中序的头节点位置，由ri将树分为左右子树
  22.         int ri = map.get(root);
  23.         TreeNode node = new TreeNode(root);
  24.         //左右指针分别指向左右子树
  25.         node.left = buildTree(is, ri - 1, ps, ps+ ri-is - 1);
  26.         node.right = buildTree(ri + 1, ie, ps + ri - is, pe - 1);
  27.         //返回根节点
  28.         return node;
  29.     }
  30. }

1.10、从前序与中序遍历序列构造二叉树

1.11、最大二叉树

生成二叉树都是相同的思路，通过递归遍历数组，生成子树，需要确认端点值 与上面的解决方式不同，此题直接使用下标进行记录，不需要使用辅助map和数组

  1.     public TreeNode constructMaximumBinaryTree(int[] nums) {
  2.         return buildTrees(nums,0, nums.length - 1);
  3.     }
  5.     TreeNode buildTrees(int[] arr,int low, int high) {
  6.         if (low>high) return null;
  7.         int max = low;
  8.         for (int i = low; i <= high; i++) {
  9.             if (arr[max]<arr[i]) max = i;
  10.         }
  11.         TreeNode node = new TreeNode(arr[max]);
  12.         node.left = buildTrees(arr,low, max-1);
  13.         node.right = buildTrees(arr,max+1, high);
  14.         return node;
  15.     }

辅助版(速度很慢)

  1. class Solution {
  2.     HashMap<Integer, Integer> maps = new HashMap<>();
  3.     int[] num;
  4.     public TreeNode constructMaximumBinaryTree(int[] nums) {
  5.         if (nums.length==0) return null;
  6.         for (int i = 0; i < nums.length; i++) {
  7.             maps.put(nums[i], i);
  8.         }
  9.         num = nums;
  10.         return buildTrees(0, nums.length - 1);
  11.     }
  13.     TreeNode buildTrees(int low, int high) {
  14.         if (low>high) return null;
  15.         int max = getMax(num, low, high);
  16.         System.out.println(max);
  17.         int ri = maps.get(max);
  18.         TreeNode node = new TreeNode(max);
  19.         node.left = buildTrees(low, ri - 1);
  20.         node.right = buildTrees(ri + 1, high);
  21.         return node;
  22.     }
  24.     int getMax(int[] arr, int low, int high) {
  25.         System.out.println("low:"+low + " high:"+high);
  26.         int max = 0;
  27.         for (int i = low; i <= high; i++) {
  28.             if (max<arr[i]) max = arr[i];
  29.         }
  30.         return max;
  31.     }
  32. }

1.12、验证搜索二叉树

思路模拟：如果是一个正确的搜索二叉树，然后按照 中序遍历 这个二叉树生成一个数组，那么数组必是有序的

  • 方法1：定义一个无限小的值，中序遍历，if（root.val>min) min=root.val else return false;
  • 方法2：双指针，定义前后指针来比较前后的值。

因此我们可以确定，此题中我们需要使用中序遍历这个二叉树

  • 递归

    1.   TreeNode pre;
    2.   public boolean isValidBST(TreeNode root) {
    3.       if (root == null) return true;
    5.       //左
    6.       boolean left = isValidBST(root.left);
    7.       if (!left) return false;
    9.       //中
    10.       //如果上一节点不为空，当前节点与上一节点比较
    11.       if (pre!=null && root.val <= pre.val) return false;
    12.       //双针织，暂存当前节点，在与下一层的值比较大小
    13.       pre = root;
    15.       //右
    16.       boolean rigtht = isValidBST(root.right);
    17.       //直接返回right
    18.       return rigtht;
    19.   }

    1.13、二叉搜索树中的众数

    用一个全局变量记录最大次数，如果当前数字的出现次数更大，则结果更新，如果相同，则插入，否则不变

  1.     ArrayList<Integer> resList = new ArrayList<>();
  2.     TreeNode pre;
  3.     int max;
  4.     HashMap<Integer, Integer> map = new HashMap<>();
  5.     public int[] findMode(TreeNode root) {
  6.         if (root==null) return null;
  7.         max = 1;
  8.         track(root);
  9.         int[] res = new int[resList.size()];
  10.         for (int i = 0; i < resList.size(); i++) {
  11.             res[i] = resList.get(i);
  12.         }
  13.         return res;
  14.     }
  16.     void track(TreeNode node) {
  17.         if (node == null) {
  18.             return;
  19.         }
  21.         track(node.left);
  22.         map.put(node.val, map.getOrDefault(node.val, 0) + 1);
  23.         if (max<map.get(node.val)){
  24.             System.out.println(map.toString());
  25.             System.out.println(max);
  26.             resList.clear();
  27.             resList.add(node.val);
  28.             max = map.get(node.val);
  29.         } else if (max == map.get(node.val)) {
  30.             resList.add(node.val);
  31.         }
  32.         pre= node;
  34.         track(node.right);
  36.     }

1.14、二叉树的最近公共祖先

本题是求最近的公共祖先，因此需要二叉树由下而上的遍历 因此需要用到后序遍历 先设想一个最理想的情况： root的左右节点分别为 p , q 此时我们利用后序遍历，如果子树中有p，q 那么直接返回 那么此时root 的左右节点不为空，root就是 p，q的最近公共祖先。 另外一种情况，当root = p 时， 按照以上逻辑直接返回p , 此时p就是p、q的最近祖先。

  1.    //递归的访问子树，并且每次返回一个节点，供上层递归判断
  2.     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
  3.         //递归返回条件，可以整合
  4.         if (root==null) return root;
  5.         if (p == root || q == root) {
  6.             return root;
  7.         }
  9.         //后序遍历，递归的访问左右节点，并用left,right 记录节点返回值
  10.         TreeNode left = lowestCommonAncestor(root.left, p,q);
  11.         TreeNode right = lowestCommonAncestor(root.right, p, q);
  13.         //left right都不为空，那么root就是最近公共节点
  14.         if (left != null && right != null) {
  15.             return root;
  16.         } else //left为空，right不为空 返回right
  17.             if (left == null && right != null) {
  18.             return right;
  19.         } else //left不为空，right为空，返回left
  20.             if (left != null && right == null) {
  21.             return left;
  22.         } else return null;
  23.     }

1.15、二叉树的插入

  1. 由于本题不限制插入形式，因此第一种方式使用最简单的直接插入

    中序遍历+双指针

  1.    TreeNode pre;
  2.     public TreeNode insertIntoBST(TreeNode root, int val) {
  3.         //root为空的特例
  4.          if (root == null && pre == null) {
  5.             return new TreeNode(val);
  6.         }
  7.         if (root == null && pre!=null) {
  8.             TreeNode node = new TreeNode(val);
  9.             if (val < pre.val) {
  10.                 pre.left = node;
  11.             }else {
  12.                 pre.right = node;
  13.             }
  14.             return pre;
  15.         }
  16.         if (val < root.val) {
  17.             pre = root;
  18.             insertIntoBST(root.left, val);         
  19.         }
  21.         if (val > root.val) {
  22.              pre = root;
  23.             insertIntoBST(root.right, val);       
  24.         }
  25.         return root;
  26.     }

直接递归

  1. class Solution {
  2.     public TreeNode insertIntoBST(TreeNode root, int val) {
  3.         if (root == null) // 如果当前节点为空，也就意味着val找到了合适的位置，此时创建节点直接返回。
  4.             return new TreeNode(val);
  6.         if (root.val < val){
  7.             root.right = insertIntoBST(root.right, val); // 递归创建右子树
  8.         }else if (root.val > val){
  9.             root.left = insertIntoBST(root.left, val); // 递归创建左子树
  10.         }
  11.         return root;
  12.     }
  13. }

迭代

  1.     public TreeNode insertIntoBST(TreeNode root, int val) {
  2.         TreeNode node =new TreeNode(val);
  3.         if (root==null) return node;
  4.         TreeNode cur = root;
  5.         TreeNode pre = root;
  6.         while (cur != null) {
  7.             pre = cur;
  8.             if (val<cur.val) cur = cur.left;
  9.             else if (val>cur.val) cur = cur.right;
  10.         }
  11.         if (pre.val>val) pre.left = node;
  12.         else pre.right = node;
  13.         return root;
  14.     }

1.16、二叉树的删除

在二叉树的删除中，主要分为四种情况

  1. 叶子：左右子树都为空
  2. 左子树为空，右子树不为空
  3. 右子树为空，左子树不为空
  4. 左右子树都不为空
  1.     public TreeNode deleteNode(TreeNode root, int key) {
  2.         if (root.val == key) {
  3.             if (root.left == null && root.right == null) {
  4.                 return null;
  5.             }
  6.             if (root.left == null && root.right != null) {
  7.                 return root.right;
  8.             }
  9.             if (root.left != null && root.right == null) {
  10.                 return root.left;
  11.             }
  12.             if (root.left != null && root.right != null) {
  13.                 TreeNode cur = root.right;
  14.                 //遍历至左目标树
  15.                 while (cur.left != null) {
  16.                     cur = cur.left;
  17.                 }
  18.                 System.out.println(root.val);
  19.                 System.out.println(cur.val);
  20.                 //最左的叶节点的左子树指向目标节点的左子树
  21.                 cur.left = root.left;
  22.                 //此时情况可视为左子树为空，右子树不为空，返回右子树
  23.                 return root.right;
  24.             }
  25.         }
  26.         if (root != null && key < root.val) {
  27.             //左子树链接
  28.             root.left = deleteNode(root.left, key);
  29.         }
  30.         if (root != null && key > root.val) {
  31.             //右子树链接
  32.             root.right = deleteNode(root.right, key);
  33.         }
  34.         return root;
  35.     }

1.17、修剪二叉搜索树

  • 返回条件：为 null 时，返回null
  • 如果当前节点值小于low，开始递归访问又节点
  • 如果大于high，则递归访问左节点
  • 连接当前节点的左右子树
  • 返回根节点
  1.     public TreeNode trimBST(TreeNode root, int low, int high) {
  2.         if (root == null) {
  3.             return null;
  4.         }
  5.         System.out.println("递归前："+root.val);
  6.         if (root.val < low) {
  7.            return trimBST(root.right, low, high);
  8.         }
  10.         if (root.val > high) {
  11.             return trimBST(root.left, low, high);
  12.         }
  14.         //对当前节点进行链接
  15.         root.left = trimBST(root.left, low, high);
  16.         root.right = trimBST(root.right, low, high);
  17.         System.out.println("递归后："+root.val);
  18.         return root;
  19.     }

1.18、完全二叉树的节点数量

在层次递归中，每层都需要遍历两端的节点，得到左右子树的深度 如果符合左右相等的条件，则符合满二叉树的条件，代入公式，然后返回结果； 如果不同则继续遍历当前层的根节点的左右子树 返回左右子树之和节点之和+1 （包含当前节点）

  1.     public int countNodes(TreeNode root) {
  2.         if (root==null) return 0;
  3.         TreeNode leftNode = root.left;
  4.         TreeNode rightNode = root.right;
  5.         int left=0,right = 0; //只记录当前层的左右节点的深度
  6.         while (leftNode != null) { //在当前层，一直往左遍历
  7.             leftNode = leftNode.left;
  8.             left++;
  9.         }
  10.         while (rightNode != null) {//在当前层，一直往右遍历
  11.             rightNode = rightNode.right;
  12.             right++;
  13.         }
  14.         if (left == right) {//根据完全二叉树性质，如果左右节点数量相等，则是满二叉树
  15.             return (2 << left - 1);
  16.         }
  17.         //如果不满足条件，则遍历左右子树然后+1
  18.         return countNodes(root.left) + countNodes(root.right)+1;
  19.     }

1.19、判断平衡二叉树

此题也是求高度问题，不过需要每层需要判断左右子树的深度只差，因此需要用到后续遍历

  1.     public boolean isBalanced(TreeNode root) {
  2.         return traceBalance(root) != -1;
  3.     }
  5.     int traceBalance(TreeNode node) {
  6.         if (node == null) {
  7.             return 0;
  8.         }
  9.         //遍历左节点
  10.         int left = traceBalance(node.left);
  11.         if (left==-1) return -1;
  13.         //遍历右节点
  14.         int right = traceBalance(node.right);
  15.         if (right==-1) return -1;
  17.         //如果当前节点的左右子树高度只差大于1
  18.         if (Math.abs(left-right)>1) return -1;
  20.         //递归从下往上返回结果，因此当前高度需要加上当前节点
  21.         return Math.max(right, left) + 1;
  22.     }

二、二刷

2.1、二叉树的直径

求直径，就是求树中每个节点左右子树深度之和的最大值 使用后序求得每个子树的左右节点之和，再返回递归的上一层

  1.     int res;
  2.     public int diameterOfBinaryTree(TreeNode root) {
  3.         res = 0;
  4.         getDeept(root);
  5.         return res-1;
  6.     }
  8.     int getDeept(TreeNode node) {
  9.         if (node==null) return 0;
  10.         int left = getDeept(node.left);
  11.         int right = getDeept(node.right);
  12.         res = Math.max(res, left + right + 1); //存取所有节点中的最大值
  13.         return Math.max(left , right )+ 1; //返回最长的边
  14.     }

2.2、将有序数组转化为二叉搜索树

由于数组已经有序，所以二叉搜索树的中序就是数组的遍历顺序，但是仅有中序序列没办法生成一个确定的树 由题意知左右子树只差不能大于1，因此取中间的元素作为根节点

  1.     public TreeNode sortedArrayToBST(int[] nums) {
  2.         return help(0, nums.length-1, nums);
  3.     }
  5.     TreeNode help(int left,int right,int[] numes) {
  6.         if (left > right) { //递归结束条件
  7.             return null;
  8.         }
  9.         int mid = (left + right) / 2;
  10.                 // System.out.println(mid);
  11.         TreeNode node = new TreeNode(numes[mid]); //创建新的节点
  12.         node.left = help(left, mid - 1, numes); // 左子树连接
  13.         node.right = help(mid + 1, right, numes); 
  14.         return node; //返回当前节点
  15.     }

2.3、二叉树的右视图

本题主要思路在于求得当前层的最右元素，主要有两种方式：

BFS

通过层次遍历，获得当前层的最后一个元素

  1.     public List<Integer> rightSideView(TreeNode root) {
  2.         ArrayList<Integer> res = new ArrayList<>();
  3.         if (root == null) {
  4.             return res;
  5.         }
  6.         Queue<TreeNode> queue = new LinkedList<>();
  7.         queue.offer(root);
  8.         while (!queue.isEmpty()) {
  9.             int size = queue.size();
  10.             for (int i = 0; i < size; i++) {
  11.                 TreeNode node = queue.poll();
  12.                 if (i == size - 1) {
  13.                     res.add(node.val);
  14.                 }
  15.                 if (node.left != null) {
  16.                     queue.offer(node.left);
  17.                 }
  18.                 if (node.right != null) {
  19.                     queue.offer(node.right);
  20.                 }
  21.             }
  22.         }
  23.         return res;
  24.     }

DFS

以 中->右->左 的方式进行遍历，每一层获取的第一个元素即为最右侧元素 在递归中引入参数深度，获得当前递归层次的深度信息 通过res.size 与 深度的比较判断是否需要加入结果集

  1.     ArrayList<Integer> res = new ArrayList<>();
  2.     public List<Integer> rightSideView(TreeNode root) {
  3.         DFS(root, 0);
  4.         return res;
  5.     }
  7.     void DFS(TreeNode node, int deep) {
  8.         if (node==null) return;
  9.         if (deep == res.size()) {
  10.             // 如果当前节点所在深度还没有出现在res里
  11.             //说明在该深度下当前节点是第一个被访问的节点
  12.             //因此将当前节点加入res中
  13.             res.add(node.val);  
  14.         }
  15.         DFS(node.right, deep + 1);
  16.         DFS(node.left, deep + 1);
  17.     }

2.4、 二叉树展开为链表

力扣

迭代+辅助栈

  1.     public void flatten(TreeNode root) {
  2.         if (root==null) return;
  3.         Deque<TreeNode> stack = new LinkedList<>();
  4.         TreeNode pre = null;
  5.         stack.offer(root);
  6.         while (!stack.isEmpty()) {
  7.             TreeNode cur = stack.pop();
  8.             if (pre != null) { //除去第一个节点，都执行以下操作
  9.                 pre.right = cur;
  10.                 pre.left = null;
  11.             }
  12.             if (cur.right != null) {
  13.                 stack.push(cur.right);
  14.             }
  15.             if (cur.left != null) {
  16.                 stack.push(cur.left);
  17.             }
  18.             pre = cur;
  19.         }
  20.     }

递归

  1. TreeNode pre = null;
  2.     public void flatten(TreeNode root) {
  3.         postOrderTraverse(root);
  4.     }
  5.     public void postOrderTraverse(TreeNode root){
  6.         if (root==null)return; // 递归终止条件
  7.         postOrderTraverse(root.right); 
  8.         postOrderTraverse(root.left);
  9.         root.left = null; //当前节点的左孩子指向空
  10.         root.right = pre; // 右节点指向pre
  11.         pre = root; //pre = root ，暂存当前节点
  12.     }

利用提题意求解

由于题目要求前序的性质不变，因此将当前节点的左孩子不为空时，左孩子必定在右孩子之上。 对于当前节点，如果其左子节点不为空，则在其左子树中找到最右边的节点， 作为前驱节点，将当前节点的右子节点赋给前驱节点的右子节点，然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。 对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。

  1.    public void flatten(TreeNode root) {
  2.         if (root == null) {
  3.             return;
  4.         }
  5.         TreeNode cur = root;
  6.         while (cur != null) {
  7.             if (cur.left != null) {
  8.                 TreeNode next = cur.left;  
  9.                 TreeNode pre = next;
  10.                 while (pre.right != null) {
  11.                     pre = pre.right;  //找到 cur.right的前驱节点
  12.                 }
  13.                 pre.right = cur.right; 
  14.                 cur.left = null;
  15.                 cur.right = next;
  16.             }
  17.             cur = cur.right;
  18.         }
  19.     }

2.5、前序中序构造二叉树

辅助map记录中序数组中值和索引的关系，辅助数组记录前序数组 采用递归遍历

  1. HashMap<Integer, Integer> map = new HashMap<>();
  2.     int[] ass;
  3.     public TreeNode buildTree(int[] preorder, int[] inorder) {
  4.         for (int i = 0; i < inorder.length; i++) {
  5.             map.put(inorder[i], i);
  6.         }
  7.         ass = preorder;
  8.         return buildTree(0, preorder.length - 1, 0, inorder.length - 1);
  9.     }
  11.     TreeNode buildTree(int preStart, int preEnd, int inStart, int inEnd) {
  12.         if (preStart > preEnd || inStart > inEnd) { //递归终止条件
  13.             return null;
  14.         }
  15.         int cur = ass[preStart];//前序数组首位即为当前需要访问的根节点
  16.         // System.out.println("----> cur："+cur);
  17.         TreeNode root = new TreeNode(cur);
  18.         int inPos = map.get(cur); //找到中序中的位置信息
  19.         // System.out.println("----> pre：" + inPos);
  20.         //位置关系可以手动推到
  21.         root.left = buildTree(preStart+1, preStart+inPos-inStart, inStart, inPos-1);
  22.         root.right = buildTree(preStart+inPos-inStart+1, preEnd, inPos+1, inEnd);
  23.         return root;
  24.     }