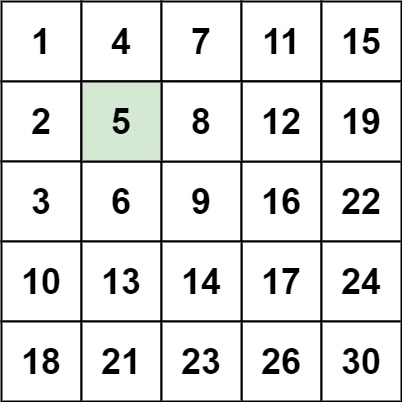
1、矩阵置 0

O(m+n)

定义长度分别为 m , n 的boolean数组，首次遍历时标记哪些数字为 0，第二次遍历时，如果辅助的数组为0，则第 i ， j 为0.

    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean[] row = new boolean[m];
        boolean[] col = new boolean[n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    row[i] = col[j] = true;
                    // System.out.println("i: " + i);
                    // System.out.println("j: " + j);
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (row[i] || col[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }

O(1)

复用原来二维数组的第一行和第一列，复用之前，先使用两个标记位判断第一行和第一列有没有为 0 的数字，其他逻辑与第一种方法类似，都是遍历然后根据标记位置0，最后根据标记位来处理第一行和第一列中为0的元素。

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean row0Flag = false, col0Flag = false;
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                col0Flag = true;
                break;
            }
        }
        for (int i = 0; i < n; i++) {
            if (matrix[0][i] == 0) {
                row0Flag = true;
                break;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                    // System.out.println("i: " + i);
                    // System.out.println("j: " + j);
                }
            }
        }
        for (int j = 1; j < n; j++) {
            if (matrix[0][j] == 0) {
                for (int i = 1; i < m; i++) {
                    matrix[i][j] = 0;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                Arrays.fill(matrix[i], 0);
            }
        }
        if (col0Flag) {
            for (int j = 0; j < m; j++) {
                matrix[j][0] = 0;
            }
        }
        if (row0Flag) {
            Arrays.fill(matrix[0], 0);
        }
    }
}

2、旋转图像

力扣

在矩阵中，可以使用矩阵的变换来解题，先以副对角线对称变换，然后再上下翻转，其次也可以主对角线翻转，然后左右翻转，本题按照副对角线进行反转

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        //副对角线变换
        for (int i = 0; i < n ; i++) {
            for (int j = 0; j < n-i; j++) { //
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][n - i - 1];  //副对角线对称
                matrix[n - j -1][n - i - 1] = temp;
            }
        }
            // System.out.println(matrix[1][2]);
        //上限对折
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j]=matrix[n - i-1][j];
                matrix[n - i-1][j] = temp;
            }
        }
    }
}

3、搜索二维矩阵 ||

力扣

根据矩阵的每行每列都有顺序的特性，让起始数字放在数组的右上角，这样就可以根据大小限制方向：

如果大于target — 下移
小于 — 左移
等于返回true

public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
          int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            }
            else {
                ++x;
            }
        }
        return false;
    }