深度优先搜索和广度优先搜索

概念

• 深度优先搜索：Depth First Search

定义：假设给定图G的初态是所有顶点均未曾访问过，在G中任选一顶点V为初始出发点（源点），则深度优先遍历可定义如下：首先访问出发点V，并将其标记为已访问过；然后依次从V出发搜索V的每个邻接点W。若W未曾访问过，则以W为新的出发点继续进行深度优先遍历，直至图中所有和源点V有路径相同的顶点（亦称为从源点可达的顶点）均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止，这里定义使用的就是递归定义。

图的深度优先遍历类似于树的前序遍历，采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索，响应地，用此方法遍历图就自然地称为图的优先遍历。

• 广度优先搜索：Breadth First Search

定义：广度优先遍历是连通图的一种遍历策略，它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域。也就是从V0出发，访问V0的各个未曾访问的邻接点W1，W2，…， Wk；然后，依次从W1,W2,… Wk出发访问各自未被访问的邻接点；

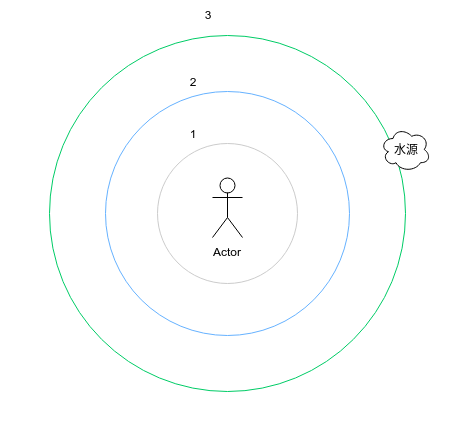
如何理解？举个例子，一个人在沙漠中，沙漠中的某处有一滩水源，这个人如果要找到这个水源怎么找？

• 采用广度优先搜索查找水源：如图所示，这个人一圈一圈的查找，直到第三圈的时候找到水源。

• 采用深度优先搜索查找水源：

深度优先搜索

深度优先搜索属于图算法的一种，是一个针对图和树的遍历算法。深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用堆数据结构来辅助实现DFS算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。

广度优先搜索

广度优先搜索是连通图的一种遍历算法，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有结点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。基本过程，BFS是从根结点开始，沿着树（图）地宽度遍历树（图）地结点。如果所有结点均被访问，则算法中止。一般用队列数据结果来辅助BFS算法。