归并排序是创建在归并操作上的一种有效的排序算法，效率为O(nlogn)。1945年由约翰.冯.诺伊曼由此提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用，且各层分治递归可以同时进行。

    图解说明：

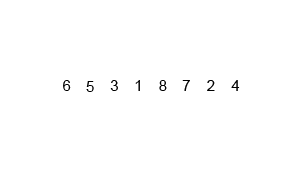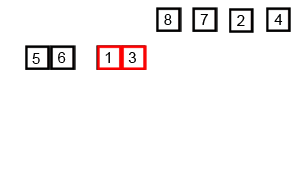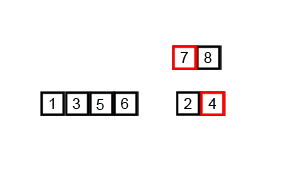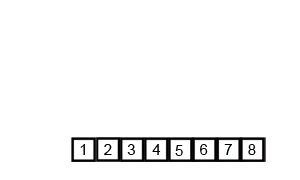
    Merge-sort-example-300px.gif

    java代码实现

    1. package com.test;
    3. /**
    4.  * 归并排序
    5.  */
    6. public class MergeSort {
    7.     public static void main(String[] args) {
    8.         int[] arr = {6, 5, 3, 1, 8, 7, 2, 4};
    9.         merge_sort(arr, 0, arr.length - 1);
    10.         for (int i : arr) {
    11.             System.out.println(i);
    12.         }
    13.     }
    15.     public static void merge_sort(int[] arr, int p, int r) {
    16.         if (p < r) {
    17.             int q = (p + r) / 2; //中间值
    18.             merge_sort(arr, p, q); //递归调用左半边，分成两组
    19.             merge_sort(arr, q + 1, r); //递归调用右半边，分成两组
    20.             merge(arr, p, q, r); //分完后排序
    21.         }
    22.     }
    24.     public static void merge(int[] arr, int p, int q, int r) {
    25.         int len = r - p + 1; //长度
    26.         int[] tmp = new int[len];  //临时数组
    27.         int i = p, j = q + 1; //两段[p, q][q+1,r]
    28.         int k = 0;
    29.         while (i <= q && j <= r) {//比较最小的存入tmp数组
    30.             if (arr[i] < arr[j]) {
    31.                 tmp[k++] = arr[i++];
    32.             } else {
    33.                 tmp[k++] = arr[j++];
    34.             }
    35.         }
    36.         //i,j其中一个已经全部放入临时数组中
    37.         while (i <= q) {
    38.             tmp[k++] = arr[i++];
    39.         }
    40.         while (j <= r) {
    41.             tmp[k++] = arr[j++];
    42.         }
    43.         //tmp赋给原数组
    44.         for (int m = 0; m < len; m++) {
    45.             arr[m + p] = tmp[m];
    46.         }
    47.     }
    48. }