Heap 堆

概念

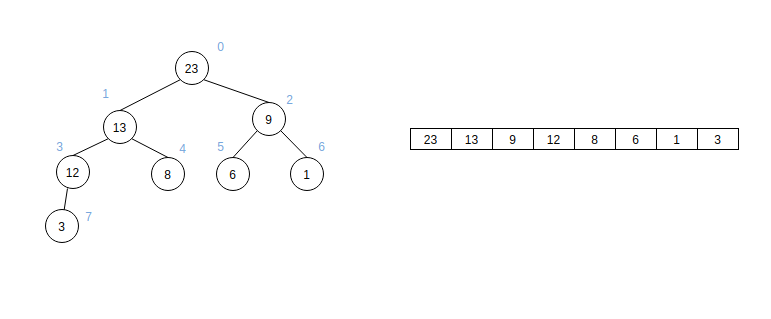
首先堆是个什么东西，从中文堆我们想到的是什么？一堆东西、草堆。其时堆就是这个东西，从下到上的物体的累计且下大上小。数据结构中的堆也是这么个东西，是用数组实现的二叉树。说到底堆还是数组，只不过按照二叉树的规则对数组进行排列。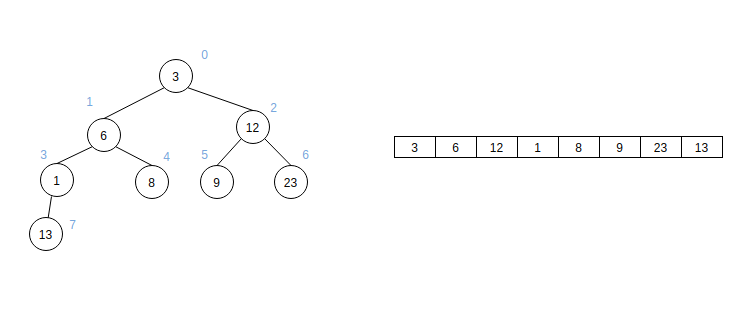

特点

• 最大堆： 父结点的值比每一个子节点的值都要大。最大的元素总是位于index 0的位值，但是最小元素未必是最后一个元素，唯一能够保证的是最小的元素是一个叶结点，但是不确定是哪一个。
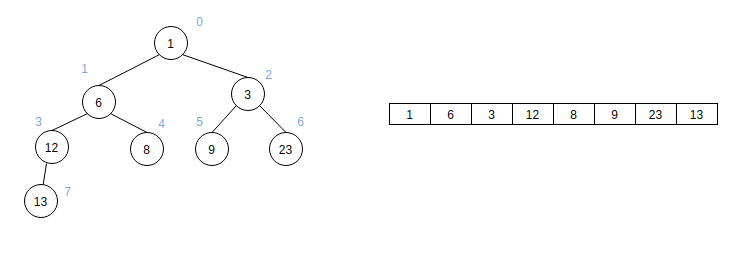
• 最小堆： 父结点的值比每一个子结点的值都要小。最小的元素总是位于index 0的位值，但是最大元素未必是最后一个元素，唯一能够保证的是最大的元素是一个叶结点，但是不确定是哪一个。

上图转换成最大堆的其中一种：

上图转换成最小堆的其中一种：

堆是数组，数组怎么能用二叉树表示？

堆的底层是数组，可是数组怎么和二叉树产生的关联？通过分析上图，我们可以得到如下的结论：

• 父结点的位值 = (子结点的位值 - 1) / 2
• 树的左结点的位值 = 父结点的位值 * 2 + 1
• 树的右结点的位值 = 父结点的位值 * 2 + 2

转换成数学公式：

• parent(i) = (i-1) / 2
• left(i) = 2i + 1
• right(i) = 2i + 2

通过这样的公式我们就可以根据数组的某个元素找到它的父结点或左右子结点。
比如这个数组arr：（上图的最小堆）

元素8的索引为4，则8的父结点为：
arr[(4 - 1) / 2]= arr[1]，即元素6
8的左子结点为：
arr[2 4 + 1] = arr[9]，数组最大索引为7，arr[9]不存在，则不存在左子结点，
8的右子结点为：
arr[2 4 + 2] = arr[10]， 不存在右子结点。