树的遍历方式

  • 前序遍历：前根遍历，按照根左右的顺序遍历
  • 中序遍历：中根遍历，按照左根右的顺序遍历
  • 后序遍历：后根遍历，按照左右根的顺序遍历

二叉排序树的概念

二叉排序树(Binary Sort Tree)，又称二叉查找树(Binary Search Tree)，也称二叉搜索树。
二叉排序树或者是一颗空树，或者是具有下列性质的二叉树：

  • 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值
  • 若右子树不空，则右子树上所有结点的值均大与或等于它的根结点的值
  • 左、右子树也分别为二叉排序树
  • 二叉排序树中每次新插入的结点一定是叶子结点。
  • 二叉排序树经过中序遍历后得到一个递增的有序序列。
  • 二叉排序树中的元素不重复。

查找

由于二叉树的递归定义性质，二叉排序树的查找同样可以使用如下递归算法查找：

  • 如果树是空的，则查找结束，无匹配。
  • 如果被查找的值和根结点的值相等，查找成功。否则就在子树中继续查找。
  • 如果被查找的值小于根结点的值就选择左子树，大于根结点的值就选择右子树。

在理想情况下，每次比较过后，树会被砍掉一半，近乎折半查找。使用中序遍历打印树，
打印出来的结果是从小到大的有序数组。

  1. /**
  2.      * 二叉排序树的搜索:
  3.      * 如果存在则返回此结点，如果不存在则返回查找路径上最后一个结点
  4.      *
  5.      * @param key
  6.      * @param tree
  7.      * @return
  8.      */
  9.     public BinarySearchTree search(int key, BinarySearchTree tree) {
  10.         if (tree == null) {
  11.             return null;
  12.         }
  13.         if (key == tree.key) {
  14.             return tree;
  15.         } else if (key < tree.key) {
  16.             return tree.left != null ? search(key, tree.left) : tree;
  17.         } else {
  18.             return tree.right != null ? search(key, tree.right) : tree;
  19.         }
  20.     }

插入

二叉排序的插入是建立在二叉排序的查找之上的，插入一个结点，就是通过查找发现该结点合适插入位置，把结点直接放进去。二叉排序树插入规则如下：

  • 若查找的key已经有在树中，则point指向该数据结点。(二叉树的key不能重复)
  • 若查找的Key没有在树中，则point指向查找路径上最后一个结点，根据情况插入最后一个结点的左子树或右子树。

图解：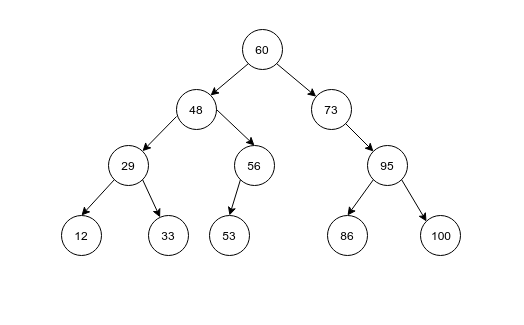
Screenshot from 2020-03-31 15-01-51.png
如果插入 56，先根据查找算法发现树中存在则不做操作，
如果插入 54，先根据查找算法没有找到k=54的结点，返回point指向53结点，发现53是叶子结点，且54 > 53，则把54插入到53的右子结点。
Screenshot from 2020-03-31 15-06-46.png

  1. /**
  2.      * 二叉排序树的插入: 不插入重复的key
  3.      *
  4.      * @param key
  5.      * @return
  6.      */
  7.     public void insert(int key) {
  8.         BinarySearchTree sub = search(key, this);
  9.         if (key != sub.key) {
  10.             BinarySearchTree node = new BinarySearchTree(key);
  11.             if (key > sub.key) {
  12.                 sub.right = node;
  13.             } else {
  14.                 sub.left = node;
  15.             }
  16.         }
  17.     }

删除

删除时需要考虑三种情况：

  • 要删除的结点是叶子结点
  • 要删除的结点只有左结点或右结点
  • 要删除的结点既有左结点又有右结点

图解：
第一种情况：要删除的结点是叶子结点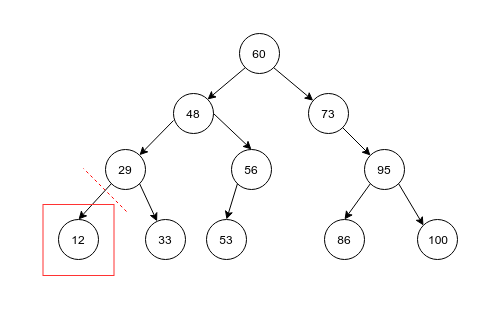
Screenshot from 2020-03-31 17-09-32.png
删除的结点是叶子结点时（left = null, right = null），则直接把双亲结点的指针移除。如上图所示，如果删除的是12结点，则29结点的left = null

  1. /**
  2.      * 删除
  3.      *
  4.      * @param key
  5.      */
  6.     public void delete(int key) {
  7.         BinarySearchTree node = search(key, this);
  8.         if (node != null) {
  9.             if (node.left == null && node.right == null) {
  10.                 BinarySearchTree parent = this.searchParent(key);
  11.                 if (parent.left != null && parent.left.equals(node)) {
  12.                     parent.left = null;
  13.                 }
  14.                 if (parent.right != null && parent.right.equals(node)) {
  15.                     parent.right = null;
  16.                 }
  17.             }
  19.         }
  20.     }

第二种情况：要删除的结点只有左结点，这种情况下也分两种情况

  • 要删除的结点为根结点，需要将根结点的root指针指向即将删除结点的左孩子，然后将删除结点的left置空即可

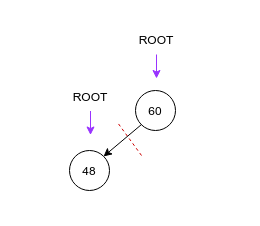
Screenshot from 2020-03-31 18-35-06.png

  • 要删除的结点不为根结点，将父结点相应的孩子指针指向删除结点的左孩子，然后将删除结点的left置空

Screenshot from 2020-03-31 18-51-43.png

第三种情况：要删除的结点只有右结点，这种情况下也有两种情况同上
Screenshot from 2020-03-31 18-54-46.png
Screenshot from 2020-03-31 18-54-51.png

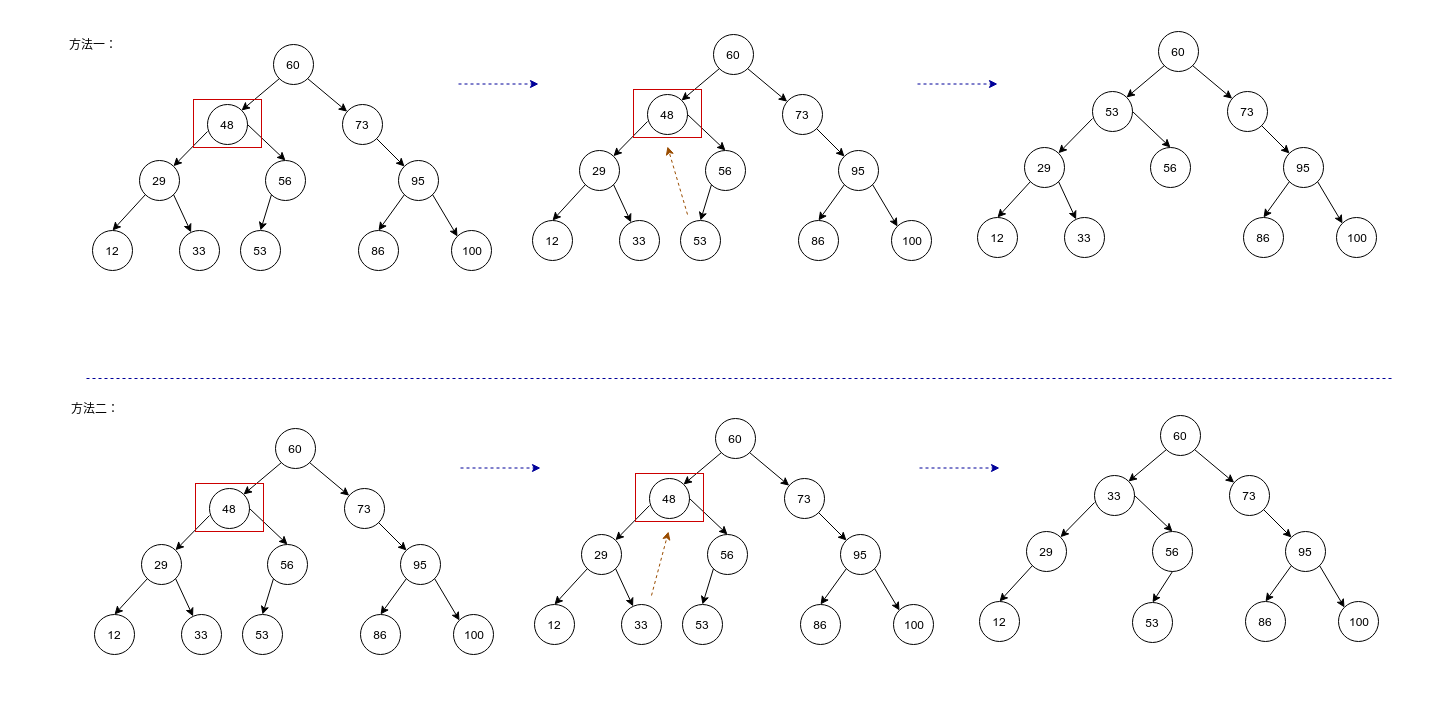
第四种情况：要删除的结点既有左结点又有右结点
查找删除结点右子树中最小的那个值（或者是左子树中最大的那个值），也就是右子树中位于最左方的那个结点（或者左子树中最右方的结点）。把查找的结点覆盖删除的结点。

Screenshot from 2020-04-01 09-14-55.png

  1. /**
  2.      * 删除
  3.      *
  4.      * @param key
  5.      */
  6.     public void delete(int key) {
  7.         BinarySearchTree node = search(key, this);
  8.         if (node != null) {
  9.             BinarySearchTree parent = this.searchParent(key);
  10.             // 叶子结点
  11.             if (node.left == null && node.right == null) {
  12.                 if (parent == null) {
  13.                     // 只有一个根结点的树，不能再删除
  14.                 } else {
  15.                     if (parent.left != null && parent.left.equals(node)) {
  16.                         parent.left = null;
  17.                     }
  18.                     if (parent.right != null && parent.right.equals(node)) {
  19.                         parent.right = null;
  20.                     }
  21.                 }
  22.             }
  23.             // 只有左结点
  24.             if (node.left != null && node.right == null) {
  25.                 if (parent == null) {
  26.                     // 此结点为根结点
  27.                     this.key = node.key;
  28.                     this.left = node.left;
  29.                     this.right = node.right;
  30.                 } else {
  31.                     if (parent.left != null && parent.left.equals(node)) {
  32.                         parent.left = node.left;
  33.                     }
  34.                     if (parent.right != null && parent.right.equals(node)) {
  35.                         parent.right = node.left;
  36.                     }
  37.                 }
  38.             }
  40.             // 只有右结点
  41.             if (node.right != null && node.left == null) {
  42.                 if (parent == null) {
  43.                     // 此结点为根结点
  44.                     this.key = node.key;
  45.                     this.left = node.left;
  46.                     this.right = node.right;
  47.                 } else {
  48.                     if (parent.left != null && parent.left.equals(node)) {
  49.                         parent.left = node.right;
  50.                     }
  51.                     if (parent.right != null && parent.right.equals(node)) {
  52.                         parent.right = node.right;
  53.                     }
  54.                 }
  55.             }
  57.             // 既有左结点又有右结点
  58.             if (node.right != null && node.left != null) {
  59.                 // 使用方法一：查找删除结点的右子树最小的结点，然后用查找的结点替换删除的结点
  60.                 BinarySearchTree min = node.right.getMin();
  61.                 this.delete(min.key);
  62.                 node.key = min.key;
  63.             }
  64.         }
  65.     }

完整代码：

  1. package com.bestlink.jh018782.tree;
  3. /**
  4.  * 二叉排序树
  5.  *
  6.  * @author jeffrey
  7.  * @date 3/31/20 3:14 PM
  8.  */
  9. public class BinarySearchTree {
  11.     private Integer key;
  13.     private BinarySearchTree left;
  15.     private BinarySearchTree right;
  17.     public Integer getKey() {
  18.         return key;
  19.     }
  21.     public BinarySearchTree getLeft() {
  22.         return left;
  23.     }
  25.     public BinarySearchTree getRight() {
  26.         return right;
  27.     }
  29.     public BinarySearchTree() {
  30.     }
  32.     public BinarySearchTree(int obj) {
  33.         this.key = obj;
  34.     }
  36.     public BinarySearchTree(int[] data) {
  37.         this.key = data[0];
  38.         for (int i = 1; i < data.length; i++) {
  39.             insert(data[i]);
  40.         }
  41.     }
  43.     /**
  44.      * 二叉排序树的搜索:
  45.      * 如果存在则返回此结点，如果不存在则返回查找路径上最后一个结点
  46.      *
  47.      * @param key
  48.      * @param tree
  49.      * @return
  50.      */
  51.     public BinarySearchTree search(int key, BinarySearchTree tree) {
  52.         if (tree == null) {
  53.             return null;
  54.         }
  55.         if (key == tree.key) {
  56.             return tree;
  57.         } else if (key < tree.key) {
  58.             return tree.left != null ? search(key, tree.left) : tree;
  59.         } else {
  60.             return tree.right != null ? search(key, tree.right) : tree;
  61.         }
  62.     }
  64.     /**
  65.      * 查找父结点
  66.      */
  67.     public BinarySearchTree searchParent(int key) {
  68.         if ((this.left != null && this.left.key == key) || (this.right != null && this.right.key == key)) {
  69.             return this;
  70.         } else {
  71.             if (this.key > key && this.left != null) {
  72.                 return this.left.searchParent(key);
  73.             } else if (this.key < key && this.right != null) {
  74.                 return this.right.searchParent(key);
  75.             }
  76.         }
  77.         return null;
  78.     }
  80.     /**
  81.      * 二叉排序树的插入: 不插入重复的key
  82.      *
  83.      * @param key
  84.      * @return
  85.      */
  86.     public void insert(int key) {
  87.         BinarySearchTree sub = search(key, this);
  88.         if (key != sub.key) {
  89.             BinarySearchTree node = new BinarySearchTree(key);
  90.             if (key > sub.key) {
  91.                 sub.right = node;
  92.             } else {
  93.                 sub.left = node;
  94.             }
  95.         }
  96.     }
  98.     /**
  99.      * 删除
  100.      *
  101.      * @param key
  102.      */
  103.     public void delete(int key) {
  104.         BinarySearchTree node = search(key, this);
  105.         if (node != null) {
  106.             BinarySearchTree parent = this.searchParent(key);
  107.             // 叶子结点
  108.             if (node.left == null && node.right == null) {
  109.                 if (parent == null) {
  110.                     // 只有一个根结点的树，不能再删除
  111.                 } else {
  112.                     if (parent.left != null && parent.left.equals(node)) {
  113.                         parent.left = null;
  114.                     }
  115.                     if (parent.right != null && parent.right.equals(node)) {
  116.                         parent.right = null;
  117.                     }
  118.                 }
  119.             }
  120.             // 只有左结点
  121.             if (node.left != null && node.right == null) {
  122.                 if (parent == null) {
  123.                     // 此结点为根结点
  124.                     this.key = node.key;
  125.                     this.left = node.left;
  126.                     this.right = node.right;
  127.                 } else {
  128.                     if (parent.left != null && parent.left.equals(node)) {
  129.                         parent.left = node.left;
  130.                     }
  131.                     if (parent.right != null && parent.right.equals(node)) {
  132.                         parent.right = node.left;
  133.                     }
  134.                 }
  135.             }
  137.             // 只有右结点
  138.             if (node.right != null && node.left == null) {
  139.                 if (parent == null) {
  140.                     // 此结点为根结点
  141.                     this.key = node.key;
  142.                     this.left = node.left;
  143.                     this.right = node.right;
  144.                 } else {
  145.                     if (parent.left != null && parent.left.equals(node)) {
  146.                         parent.left = node.right;
  147.                     }
  148.                     if (parent.right != null && parent.right.equals(node)) {
  149.                         parent.right = node.right;
  150.                     }
  151.                 }
  152.             }
  154.             // 既有左结点又有右结点
  155.             if (node.right != null && node.left != null) {
  156.                 // 使用方法一：查找删除结点的右子树最小的结点，然后用查找的结点替换删除的结点
  157.                 BinarySearchTree min = node.right.getMin();
  158.                 this.delete(min.key);
  159.                 node.key = min.key;
  160.             }
  161.         }
  162.     }
  164.     /**
  165.      * 递归查询结点的最左侧结点(最小的结点)
  166.      * @return
  167.      */
  168.     public BinarySearchTree getMin() {
  169.         if (this.left == null) {
  170.             return this;
  171.         } else {
  172.             return this.left.getMin();
  173.         }
  174.     }
  176.     /**
  177.      * 递归查询结点的最右侧结点(最大的结点)
  178.      * @return
  179.      */
  180.     public BinarySearchTree getMax() {
  181.         if (this.right == null) {
  182.             return this;
  183.         } else {
  184.             return this.right.getMax();
  185.         }
  186.     }
  188.     /**
  189.      * 获取树的深度
  190.      *
  191.      * @param tree
  192.      * @return
  193.      */
  194.     public int getDepth(BinarySearchTree tree) {
  195.         return tree == null ? 0 : (1 + Math.max(getDepth(tree.left), getDepth(tree.right)));
  196.     }
  198.     /**
  199.      * 打印整颗树
  200.      */
  201.     public void print() {
  202.         // 得到树的深度
  203.         int treeDepth = getDepth(this);
  204.         // 最后一行的宽度为2的（n - 1）次方乘3，再加1
  205.         // 作为整个二维数组的宽度
  206.         int arrayHeight = treeDepth * 2 - 1;
  207.         int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
  208.         // 用一个字符串数组来存储每个位置应显示的元素
  209.         String[][] res = new String[arrayHeight][arrayWidth];
  210.         // 对数组进行初始化，默认为一个空格
  211.         for (int i = 0; i < arrayHeight; i++) {
  212.             for (int j = 0; j < arrayWidth; j++) {
  213.                 res[i][j] = " ";
  214.             }
  215.         }
  217.         // 从根节点开始，递归处理整个树
  218.         // res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0');
  219.         writeArray(this, 0, arrayWidth / 2, res, treeDepth);
  221.         // 此时，已经将所有需要显示的元素储存到了二维数组中，将其拼接并打印即可
  222.         for (String[] line : res) {
  223.             StringBuilder sb = new StringBuilder();
  224.             for (int i = 0; i < line.length; i++) {
  225.                 sb.append(line[i]);
  226.                 if (line[i].length() > 1 && i <= line.length - 1) {
  227.                     i += line[i].length() > 4 ? 2 : line[i].length() - 1;
  228.                 }
  229.             }
  230.             System.out.println(sb.toString());
  231.         }
  232.     }
  234.     private static void writeArray(BinarySearchTree currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
  235.         // 保证输入的树不为空
  236.         if (currNode == null) {
  237.             return;
  238.         }
  239.         // 先将当前节点保存到二维数组中
  240.         res[rowIndex][columnIndex] = String.valueOf(currNode.key);
  242.         // 计算当前位于树的第几层
  243.         int currLevel = ((rowIndex + 1) / 2);
  244.         // 若到了最后一层，则返回
  245.         if (currLevel == treeDepth) {
  246.             return;
  247.         }
  248.         // 计算当前行到下一行，每个元素之间的间隔（下一行的列索引与当前元素的列索引之间的间隔）
  249.         int gap = treeDepth - currLevel - 1;
  251.         // 对左儿子进行判断，若有左儿子，则记录相应的"/"与左儿子的值
  252.         if (currNode.left != null) {
  253.             res[rowIndex + 1][columnIndex - gap] = "/";
  254.             writeArray(currNode.left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
  255.         }
  257.         // 对右儿子进行判断，若有右儿子，则记录相应的"\"与右儿子的值
  258.         if (currNode.right != null) {
  259.             res[rowIndex + 1][columnIndex + gap] = "\\";
  260.             writeArray(currNode.right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
  261.         }
  262.     }
  263. }

测试用例：

  1. package com.bestlink.jh018782;
  3. import com.bestlink.jh018782.tree.BinarySearchTree;
  4. import org.junit.jupiter.api.Test;
  6. /**
  7.  * @author jeffrey
  8.  * @date 3/31/20 3:56 PM
  9.  */
  10. public class BinarySearchTreeTest {
  12.     @Test
  13.     public void test() {
  14.         int[] arr = new int[]{60, 48, 73, 29, 56, 95, 12, 33, 53, 86, 100};
  15.         // 转换
  16.         BinarySearchTree tree = new BinarySearchTree(arr);
  17.         tree.print();
  18.         System.out.println();
  19.         // 插入
  20.         tree.insert(90);
  21.         tree.insert(31);
  22.         tree.print();
  23.         // 删除
  24.         tree.delete(95);
  25.         tree.print();
  26.     }
  27. }