1.Union: 查看两个元素之间是否可连接

  • 判断网络中节点连接问题

  • 路径问题

    2.并查集的实现：

    并查集中并不保存实际元素，而是元素与索引进行一一映射

    1. // UF 接口
    2. public interface UF {
    3.   int getSize();
    4.   // 查看两个元素可连接
    5.   boolean isConnected(int p, int q);
    6.   void unionElements(int p, int q);
    7. }
    1. // 并查集使用 Tree 实现
    2. public class UnionFind implements UF{
    3.   // index 对应元素，存储的值为集合的id
    4.   private int[] id;
    5.   // 先初始化传入的并查集大小，之后的再说
    6.   public UnionFind(int[] arr){
    7.       id = new int[arr.length];
    8.       for(int i = 0; i < arr.length; i++){
    9.           id[i] = i;
    10.       }
    11.   }
    13.   // 获取size
    14.  @Override
    15.   public int getSize(){
    16.       return id.length;
    17.   }
    19.   // 查看索引对应的集合
    20.   public int find(int index){
    21.       if (index < 0 || index > id.length) {
    22.               throw new IllegalArgumentException("out of index");
    23.           }
    24.           return id[index];
    25.   }
    27.   // 查看两个元素可连接
    28.   @Override
    29.   public boolean isConnected(int p, int q){
    30.       return find(p) == find(q);
    31.   }
    33.   @Override
    34.   // 修改其中一个节点的ID
    35.   // 之后需要将所有均改为同一ID
    36.   public void unionElements(int p, int q){
    37.       int pID = find(p);
    38.       int qID = find(p);
    39.       if(qId == pID){
    40.           return;
    41.       }
    42.       for(int i = 0; i < id.length(); i++){
    43.           if(find[i] == qID){
    44.               find[i] = pID;
    45.           }
    46.       }  
    47.   }
    48. }

    // 这时候 isConnected() 的时间复杂度为O(1)
    // 而 unionElement() 为 O(n)

    3.优化

  • 引入父节点，这样每次就只需要修改父节点对应的上一级 节点

    1. // 注意此时 root 节点对应的上一个父节点就是他本身
    2. public class UnionFind implements UF{
    3.   // 存储 索引对应的父节点
    4.   private int[] parent;
    5.   // 先初始化传入的并查集大小，之后的再说
    6.   public UnionFind(int[] arr){
    7.       parent = new int[arr.length];
    8.       for(int i = 0; i < arr.length; i++){
    9.           parent[i] = i;
    10.       }
    11.   }
    13.   // 获取size
    14.  @Override
    15.   public int getSize(){
    16.       return parent.length;
    17.   }
    19.   // 查看索引对应的集合
    20.   public int find(int index){
    21.       if (index < 0 || index > id.length) {
    22.               throw new IllegalArgumentException("out of index");
    23.           }
    24.       // 要找到 root ，返回 所属的 root 对应的结合ID
    25.       // root 节点的值与自身索引相同
    26.       while(index != parent[index]){
    27.               index = parent[index];
    28.       }
    29.       return index;
    30.   }
    32.   // 查看两个元素可连接
    33.   @Override
    34.   public boolean isConnected(int p, int q){
    35.       return find(p) == find(q);
    36.   }
    38.   @Override
    39.   // 修改其中一个节点的ID
    40.   // 之后需要将所有均改为同一ID
    41.   public void unionElements(int p, int q){
    42.        // 获取父节点
    43.       int pParent = find(p);
    44.       int qParent = find(q);
    46.       // 如果两节点相同
    47.       if(pParent == qParent){
    48.           return;
    49.       }else{
    50.           // 其中一个元素的父亲节点变指向另一个元素
    51.           parent[p] = qParent;
    52.       }
    53.   }
    54. }

    // 此时 find() 的 时间复杂度为 O(h)
    // unionElements() 的时间复杂度为 O(h)

  • 使用 size() 进行优化

  • 由于时间复杂度与树的高度有关，所以size() 最好

    1. // 注意此时 root 节点对应的上一个父节点就是他本身
    2. public class UnionFind implements UF{
    3.   // 存储 索引对应的父节点
    4.   private int[] parent;
    5.   private int[] sz;
    6.   // 先初始化传入的并查集大小，之后的再说
    7.   public UnionFind(int[] arr){
    8.       parent = new int[arr.length];
    9.       for(int i = 0; i < arr.length; i++){
    10.           parent[i] = i;
    11.           sz[i] = 1;
    12.       }
    13.   }
    15.   // 获取size
    16.  @Override
    17.   public int getSize(){
    18.       return parent.length;
    19.   }
    21.   // 查看索引对应的集合
    22.   public int find(int index){
    23.       if (index < 0 || index > id.length) {
    24.               throw new IllegalArgumentException("out of index");
    25.           }
    26.       // 要找到 root ，返回 所属的 root 对应的结合ID
    27.       // root 节点的值与自身索引相同
    28.       while(index != parent[index]){
    29.               index = parent[index];
    30.       }
    31.       return index;
    32.   }
    34.   // 查看两个元素可连接
    35.   @Override
    36.   public boolean isConnected(int p, int q){
    37.       return find(p) == find(q);
    38.   }
    40.   @Override
    41.   // 修改其中一个节点的ID
    42.   // 之后需要将所有均改为同一ID
    43.   public void unionElements(int p, int q){
    44.        // 获取父节点
    45.       int pParent = find(p);
    46.       int qParent = find(q);
    48.       // 如果两节点相同
    49.       if(pParent == qParent){
    50.           return;
    51.       }else{
    52.           if(sz[qParent] > sz[pParent]){
    53.               sz[qParent] += sz[pParent];
    54.               parent[pParent] = qParent;
    55.           }else{
    56.               sz[pParent] += sz[qParent];
    57.               parent[qParent] = pParent;             
    58.           }
    59.       }
    60.   }
    61. }

  • 使用 rank(）树的高度优化

    1. blic class UnionFind implements UF{
    2.   // 存储 索引对应的父节点
    3.   private int[] parent;
    4.   private int[] rank;
    5.   // 先初始化传入的并查集大小，之后的再说
    6.   public UnionFind(int[] arr){
    7.       parent = new int[arr.length];
    8.       rank = new int[arr.length];
    9.       for(int i = 0; i < arr.length; i++){
    10.           parent[i] = i;
    11.           rank[i] = 1;
    12.       }
    13.   }
    15.   // 获取size
    16.  @Override
    17.   public int getSize(){
    18.       return parent.length;
    19.   }
    21.   // 查看索引对应的集合
    22.   public int find(int index){
    23.       if (index < 0 || index > id.length) {
    24.               throw new IllegalArgumentException("out of index");
    25.           }
    26.       // 要找到 root ，返回 所属的 root 对应的结合ID
    27.       // root 节点的值与自身索引相同
    28.       while(index != parent[index]){
    29.               index = parent[index];
    30.       }
    31.       return index;
    32.   }
    34.   // 查看两个元素可连接
    35.   @Override
    36.   public boolean isConnected(int p, int q){
    37.       return find(p) == find(q);
    38.   }
    40.   @Override
    41.   // 修改其中一个节点的ID
    42.   // 之后需要将所有均改为同一ID
    43.   public void unionElements(int p, int q){
    44.        // 获取父节点
    45.       int pParent = find(p);
    46.       int qParent = find(q);
    48.       // 如果两节点相同
    49.       if(pParent == qParent){
    50.           return;
    51.       }else{
    52.           if(rank[qParent] > rank[pParent]){
    53.               parent[pParent] = qParent;
    54.           }else if(rank[qParent] < rank[pParent]){
    55.               parent[qParent] = pParent;   
    56.           }else{
    57.               parent[pRoot] = qRoot;
    58.               rank[qRoot] +=1;
    59.           }
    60.       }
    61.   }
    62. }

  • 直接让 索引的上移节点指向 root 节点，减少高度 , 进行路径压缩

  • 让同一高度下，子节点数较多

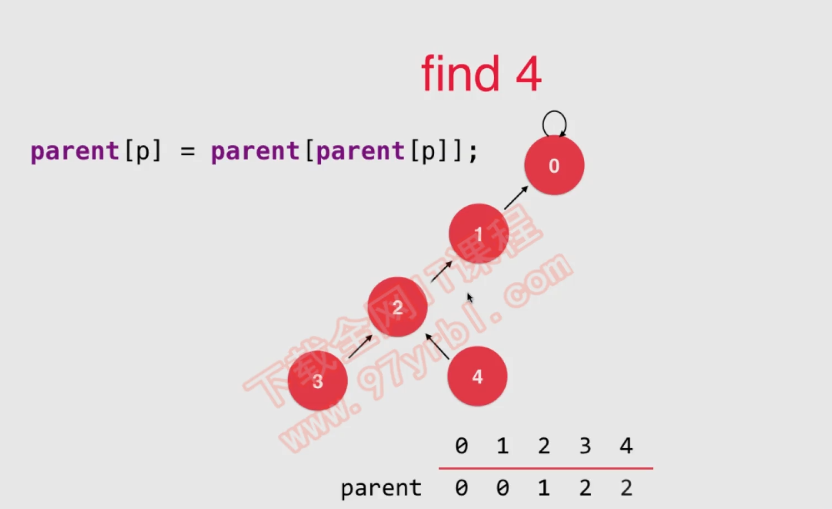
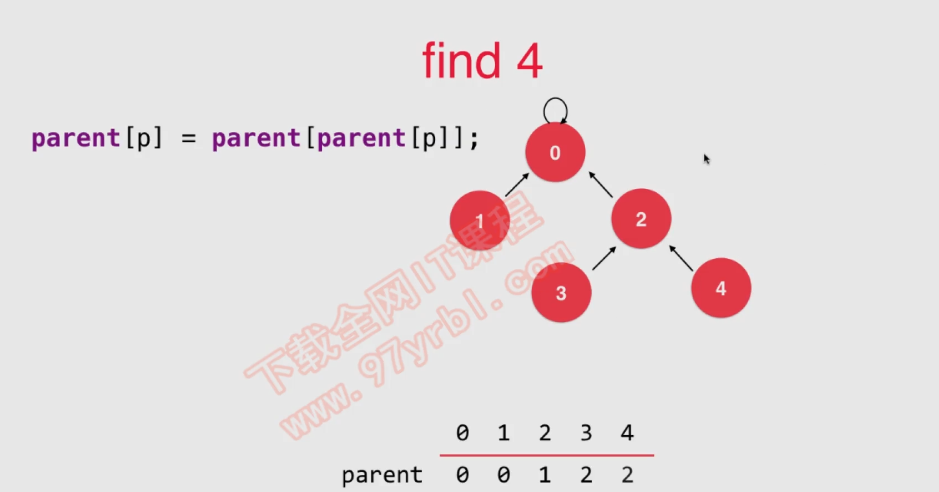
image.png
image.png

// 在查找过程中进行的优化
public int find(int index){
        if (index < 0 || index > id.length) {
                throw new IllegalArgumentException("out of index");
            }
        // 要找到 root ，返回 所属的 root 对应的结合ID
        // root 节点的值与自身索引相同
        while(index != parent[index]){
            parent[index] = parent[parent[index]];
            index = parent[index];
        }
        return index;
    }