一、Stack:

  • 一种线性结构，栈的操作为数组的子集
  • 只能从一端添加元素，一端取出元素
  • 栈是一种后进先出的数据结构

    1.栈的应用：

  1. 撤销操作 2.程序调用的系统栈

    2.具体实现：

    使用数组实现

    1. public class Stack<E>{
    2.  private int size;
    3.  private E[] data;
    5.  // 直接指定capacity
    6.  public Stack(){
    7.      data = (E[]) new Object[capacity];
    8.      size = 0;
    9.  }
    11.  // 数组扩容或者缩小
    12.  public E[] resize(int capacity){
    13.      E[] temp = (E[]) new Object[capacity];
    14.      for(int i = 0; i < size; i++){
    15.          temp[i] = data[i];
    16.      }
    17.      data = temp;
    18.      return data;
    19.  }
    21.  // 添加元素
    22.  public void push(E e){
    23.      if(size == data.length){
    24.          resize(2 * data.length);
    25.      }
    26.      data[size] = e;
    27.      size++;
    28.  }
    30.  // 获取栈顶元素
    31.  public E peek(){
    32.      return data[size - 1];
    33.  }
    35.  // 弹出栈顶元素
    36.  public E pop(){
    37.      if(size == 0){
    38.          throw new IlleageArgumentAccess("empty Stack");
    39.      }
    40.      E res = data[size - 1];
    41.      data[size - 1] = null;
    42.      size--;
    43.      if(size == (data.length/4 ) && size/2 != 0){
    44.          resize(data.length/2);
    45.      }
    46.      return res;
    47.  }
    49.  // 获取数组内元素个数
    50.  public int getSize(){
    51.      return size;
    52.  }
    54.  public boolean isEmpty(){
    55.      return size == 0;
    56.  }
    57. }

    3.栈中应用的复杂度分析：

  • void push O(1) 均摊
  • E pop() O(1) 均摊
  • E peek() O(1)
  • int getSize() O(1)

  • boolean isEmpty() O(1)

    4.括号匹配（编译器）：

    相关leetcode问题 ： https://leetcode-cn.com/problems/valid-parentheses/
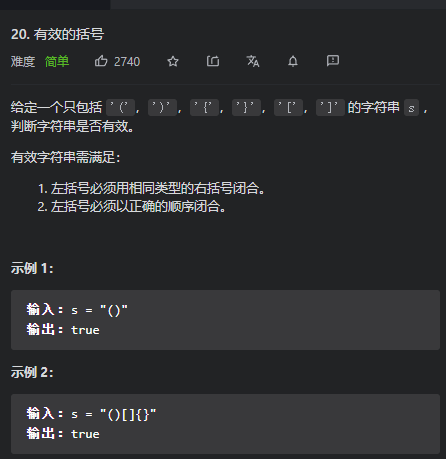
    image.png

    1. class Solution {
    2.   public boolean isValid(String s) {
    3.       Stack<Character> stack = new Stack();
    4.       for(int i = 0; i<s.length();i++){
    5.           char c = s.charAt(i);
    6.           if(c == '(' || c == '[' || c=='{'){
    7.               stack.push(c);
    8.           }else{
    9.               if(stack.isEmpty()){
    10.                   return false;
    11.               }
    12.               char topChar = stack.pop();
    13.               if(c == ')' && topChar!='(' || c == '}' && topChar!='{'|| c == ']' && topChar!='['){
    14.                   return false;
    15.               }
    16.           }
    17.       }
    18.       return stack.isEmpty();
    19.   }
    20. }

    二、Queue（队列）

    实际上是一个接口，通常由LinkedList 实现

  • 也是数据结构，同样操作也是数组的子集

  • 只能从队尾添加元素，从队首取出元素
  • 多使用链表实现

image-20211007192231245.png

  • 队列的各种操作的复杂度分析

    • void enqueue(E) O(1) 从尾部添加元素 addLast（）
    • E dequeue() O(n) 从队首删除元素 removeFirst()
    • E front() O(1)
    • int getSize() O(1)

    • boolean isEmpty() O(1)

      1. public class Queue<E>{
      2. private int size;
      3. private E[] data;
      5. public Queue(){
      6.    data = (E[]) new Object[15];
      7.    size = 0;
      8. }
      10. // resize 数组
      11. public E[] resize(int capacity){
      12.    E[] temp = (E[]) new Object[capacity];
      13.    for(int i = 0; i < size; i++){
      14.        temp[i] = data[i];
      15.    }
      16.    data = temp;
      17.    return data;
      18. }
      20. // 入队操作
      21. public void enqueue(E e){
      22.    if(size == data.length){
      23.        resize(2*data.length);
      24.    }
      25.    data[size] = e;
      26.    size++;
      27. }
      29. // 出队操作
      30. public E dequeue(){
      31.    if(size == 0){
      32.        throw new IllegalArgumentException("empty Stack");
      33.    }
      34.    E res = data[0];
      35.    for(int i = 0; i < size - 1; i++){
      36.        data[i] = data[i+1];
      37.    }
      38.    data[size - 1] = data[size];
      39.    size--;
      40.    return res;
      41. }
      43. // 队首元素
      44. public E front(){
      45.    return data[0];
      46. }
      48. // 获取元素个数
      49. public int getSize(){
      50.    return size;
      51. }
      53. // 查看是否为空
      54. public boolean isEmpty(){
      55.    return size==0;
      56. }
      58. // 从尾部添加元素
      59. public void addLast(E e){
      60.    enqueue(e);
      61. }
      63. // 从队首删除元素
      64. public E removeLast(){
      65.    return dequeue();
      66. }
      67. }

      三、循环队列（记录队首）

  • front / tail

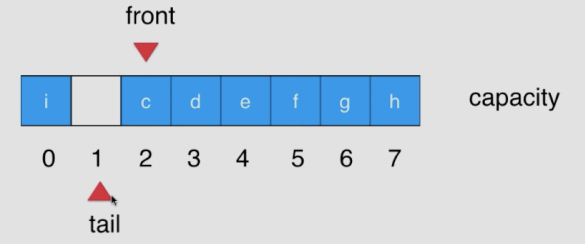
image-20211007201244134.png

  • front == tail (队列为空) | | (tail + 1) % c == front （队列为满）

  • 对于循环队列的出队操作 dequeue() 复杂度为O (1) ```java // 实现方法 ： 1.浪费一个空间 2.不浪费一个空间 // 循环数组需要确定头节点与尾结点，因为此时头和尾不再是 0 和 data.length - 1 public LoopQueue{ private int size; private E[] data; private int front, tail;

    public LoopQueue(){

    1.  data = (E[]) new Object[15];
    2.  size = 0;
    3.  front = 0;
    4.  tail = 0;

    }

    // 对数组进行扩容 private E[] resize(int capacity){

    1.  E[] temp = (E[]) new Object[capacity];
    2.  for(int i = 0; i < data.lenght; i++){
    3.      temp[i] = data[(i+front)%(data.length)];
    4.  }
    5. data = temp;
    6. front = 0;
    7. tail = data.length - 1;
    8. return data;

    }

    // 队尾入栈 enqueue public void enqueue(E e){

    1.  if(size == data.length){
    2.      resize(2*data.length);
    3.  }
    4.  data[tail] = e;
    5.  tail = (tail + 1) % data.length;
    6.  size++;

    }

    // 队首出栈 dequeue public E dequeue(){

    1.     if(size ==  0){
    2.      throw new IllegalArgumentException("Queue is empty");
    3.  }
    4.  data[front] = null;
    5.  front = (front + 1) % data.length;
    6.  size--;
    7.  if(size == getCapacity() /4 && getCapacity()/2!=0){
    8.      resize(getCapacity()/2);
    9.  }
    10.  return res;

    }

    // 获得栈内元素个数 public int getSize(){

    1.  return size;

    }

    // 获取队首元素 public E getFirst(){

    1.  return data[front];

    }

    // 获取队尾元素 public E getLast(){

    1.  return data[tail];

    }

    // 查看数组是否为空 public boolean isEmpty(){

    1.  return size == 0;

    }

}

  1. <a name="8dc02c70"></a>
  2. ## 四、数组队列与循环队列的复杂度分析
  3. 实际上 浪费空间使用 size() 是为了，保证 tali == front 时可以判断非空还是非满，假如不使用size 的话如何实现<br />使用无 size进行实现<br />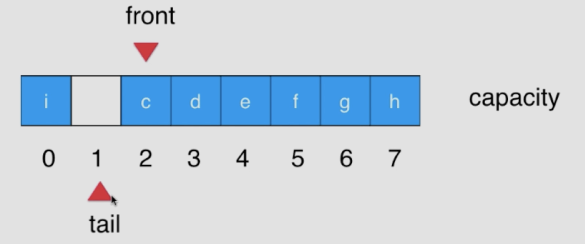![image-20211007201244134.png](https://cdn.nlark.com/yuque/0/2021/png/190166/1635579117334-9703a71b-10e8-4580-a443-41b5f8c3379a.png#clientId=uff1bc9d2-35c4-4&from=drop&id=u04e6aa36&margin=%5Bobject%20Object%5D&name=image-20211007201244134.png&originHeight=244&originWidth=585&originalType=binary&ratio=1&size=23453&status=done&style=none&taskId=u87d7e189-4809-4a41-bd68-b85ed497121)
  5. 但是实际上，tail !=  front , 主要是因为， 在 enqueue 的时候， 使用size的是先把元素填进去之后，再改变tail。 假设 capacity  = 3, 实际为4；<br />arr [ tail  =  0 ] = 1 ; tail ++ = 1;      arr [ tail  =  1 ] = 2 ; tail ++ = 2;<br />arr [ tail  =  2 ] = 3 ; tail ++ = 3;     此时 (tail +  1) % data.length == 0, 进行resize() ;       即 index = 3 的空间没有用到。  此时使用 size 是因为 tail  超前++ ； 存在空值，可以直接使用size++ 计算数量
  6. <a name="98848ff9"></a>
  7. ## 五、双端队列（Deque）:
  8. 可以在两端添加元素，也可以在队列的两端删除元素<br />addFront() / addLast()<br />removeFront() / removeLast()
  9. ```java
  10. // 实现 Deque
  11. public class Deque<E>{
  12.     public void addFront(){
  13.         if(size == data.length){
  14.             resize(2*data.length);
  15.         }
  16.         if(front == 0){
  17.             front = (front - 1 + data.length);
  18.             data[front] = e;
  19.         } else {
  20.             front = front - 1;        
  21.             data[front] = e;
  22.         }
  23.         size++;
  24.     }
  26.     public E removeLast(){
  27.         if(size == 0){
  28.             throw new IllegalArgumentException("Queue is empty");
  29.         }
  30.            E res;
  31.         if(tail == 0){
  32.             tail = tail - 1 + data.length;
  33.                res = data[tail];
  34.             data[tail] = null;
  35.         }  else {
  36.             tail = tail - 1;
  37.             data[tail] = null;
  38.         }
  39.         size--;
  40.         return res;
  41.     }
  42. }

六、使用动态数组实现栈和队列

image-20211009150656593.png

https://leetcode-cn.com/problems/implement-stack-using-queues/ 用队列实现栈
image.png

// 后入先出
class MyStack {
    private Queue<Integer> queue1;
    private Queue<Integer> queue2;
    public MyStack(){
        queue1 = new LinkedList<Integer>;
        queue2 = new LinkedList<Integer>;
    }

    public void push(int x){
        while(!queue1.isEmpty()){
            queue2.add(queue1.poll());
        }
        queue1.add(x);
        while(!queue2.isEmpty()){
            queue1.add(queue2.poll());
        }
    }

    public int pop(){
        return queue1.poll();
    }

       public int top(){
        return queue1.peek();
    }

    public boolean empty(){
        return queue1.isEmpty();
    }
}

https://leetcode-cn.com/problems/implement-queue-using-stacks/ 用栈实现队列
image.png

// 先入先出
class MyQueue {
    private Stack<Integer> stack;
    private Stack<Integer> stack1;

    public MyQueue() {
        stack = new Stack<Integer>();
        stack1 = new Stack<Integer>();
    }

    public void push(int x) {
        while(!stack.isEmpty()){
            stack1.add(stack.pop());
        }
        stack.add(x);
        while(!stack1.isEmpty()){
            stack.add(stack1.pop());
        }
    }

    public int pop() {
        return stack.pop();
    }

    public int peek() {
        return stack.peek();
    }

    public boolean empty() {
        return stack.isEmpty();
    }
}