1.线段树：

  • 线段树中，叶子节点为数组的元素，线段树中的其他非叶子节点为区间内的最大或者最小/或者总和（根据具体业务而定）

（1）区间染色问题：有一面墙，长度为n，每次选择一段墙染色，m次操作后，问区间[i,k]有多少次颜色。
（2）区间查询

2.线段树的二叉：

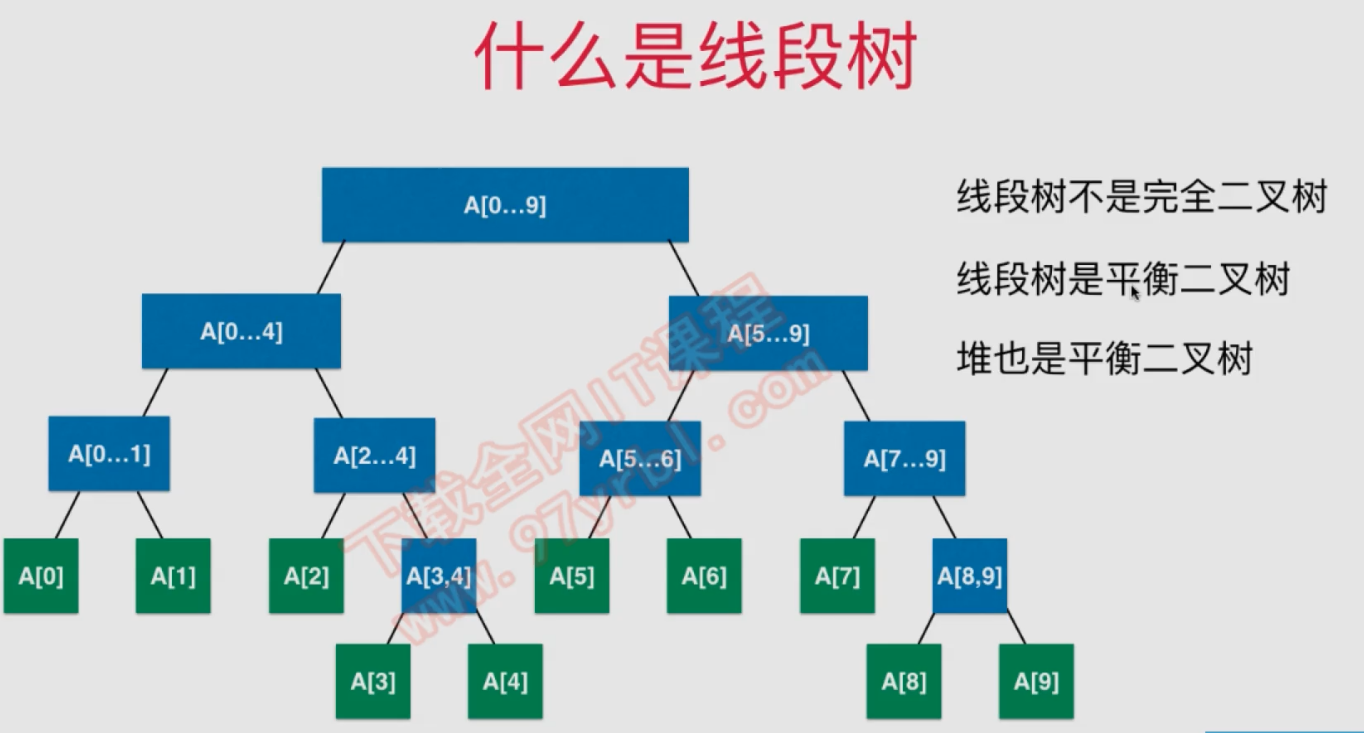
image.png

  • 平衡二叉树下，二叉搜索不会退化为链表，平衡二叉树的最大深度与最小深度差距不超过1

    3.线段树的实现：

  • 采用数组实现：假如有 n 个元素， 则上一层节点有 n / 2 个节点，故需要 4n 空间

    1. // 使用数组实现线段树
    2. public class Set<E extends Comparable<E>>{
    3.   private E[] data;
    4.   private E[] tree;
    5.   private Merger<E> merger;
    7.   public Set(E[] arr, Merger<E> merger){
    8.       data = (E[]) Object[arr.length];
    9.       for(int i = 0 ; i < arr.length; i++){
    10.           data[i] = arr[i];
    11.       }
    12.       tree = (E[]) Object[4 * arr.length];
    13.       // 建立线段树
    14.       buildSegTree(0, 0, data.length - 1);
    15.   }
    17.   public int leftChild(int index){
    18.       return 2 * index + 1;
    19.   }
    21.   public int rightChild(int index){
    22.       return 2 * index + 2;
    23.   }
    25.   public int parent(int index){
    26.       return index - 1 / 2;
    27.   }
    29.   public void buildSegTree(int treeIndex, int l, int r){
    30.       if(l == r){
    31.           tree[treeIndex] = data[l];
    32.           return;
    33.       }
    34.       // 每次下一个节点都是 [l, mid][mid + 1, r]
    35.       int mid = l + (r - l) / 2;
    36.       buildSegTree(leftChild(treeIndex), l, mid);
    37.       buildSegTree(rightChild(treeIndex), mid + 1, r);
    38.       tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
    39.   }
    41.   // 区间查询
    42.   public E Query(int QueryL, int QueryR){
    43.       if(QueryL < 0 || QueryL >= data.length || QueryR < 0 || QueryR >=data.length){
    44.           throw new IllegealmentException(" out of index");
    45.       }
    46.       E res = Query(0 , 0, data.length, QueryL, QueryR);
    47.       return res;
    48.   } 
    50.   // 从 root 开始，在 [0, data.length - 1] 中查询 QueryL ~ QueryR 
    51.   private E query(int treeIndex, int l, int r, int QueryL, int QueryR){
    52.       if(l == QueryL && r == QueryR)
    53.           return tree[treeIndex];
    54.       int mid = l + (r - l) / 2;
    55.       if(QueryR <=mid){
    56.           return query(leftChild(treeIndex), l, mid, QueryL ,Query R);
    57.       }else if(QueryL >= mid + 1){
    58.           return query(rightChild(treeIndex), mid+1, r, QueryL, QueryR);
    59.       }else{ // QueryL <= mid && QueryR >= mid
    60.           return merger.merge(query(leftChild(treeIndex), l, mid, QueryL, mid), query(rightChild(treeIndex), mid+1, r, mid + 1, r));
    61.       }
    62.   }
    64.   // 更改数值，更改数组某index 的元素
    65.   public void set(int index, E value){
    66.       if(index < 0 || index >= data.length){
    67.           throw new IllegalException("out of index");
    68.       }
    69.       set(0, 0, data.length - 1, index, value);
    70.   }
    72.   public void set(int treeIndex, int l, int r, int index, E value){
    73.       if(l == r){
    74.           tree[treeIndex] = value;
    75.       }
    76.       int mid = l + (r - l) / 2;
    77.       if(index >= mid + 1){
    78.           set(rightChild(treeIndex), mid + 1, r, index, value);            
    79.       }else if(index <= mid){
    80.           set(leftChild(treeIndex), l, mid, index, value);
    81.       }
    82.       tree[treeIndex] = merger.merge(tree[leftchild(treeIndex)], tree[rightchild(treeIndex)]);
    83.   }
    84. }

4.线段树的区间更新：

  • 最好使用lazy[] 区间记录未更新内容，等下一次需要更新的时候，再把lazy[] 传入更新，要不频繁更新开销太大。

    5.线段树的练习：

    leetcode 303, leetcode 307