基本概念

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。希尔排序是把记录按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

算法描述

我们来看下希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
按增量序列个数k，对序列进行k 趟排序；
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。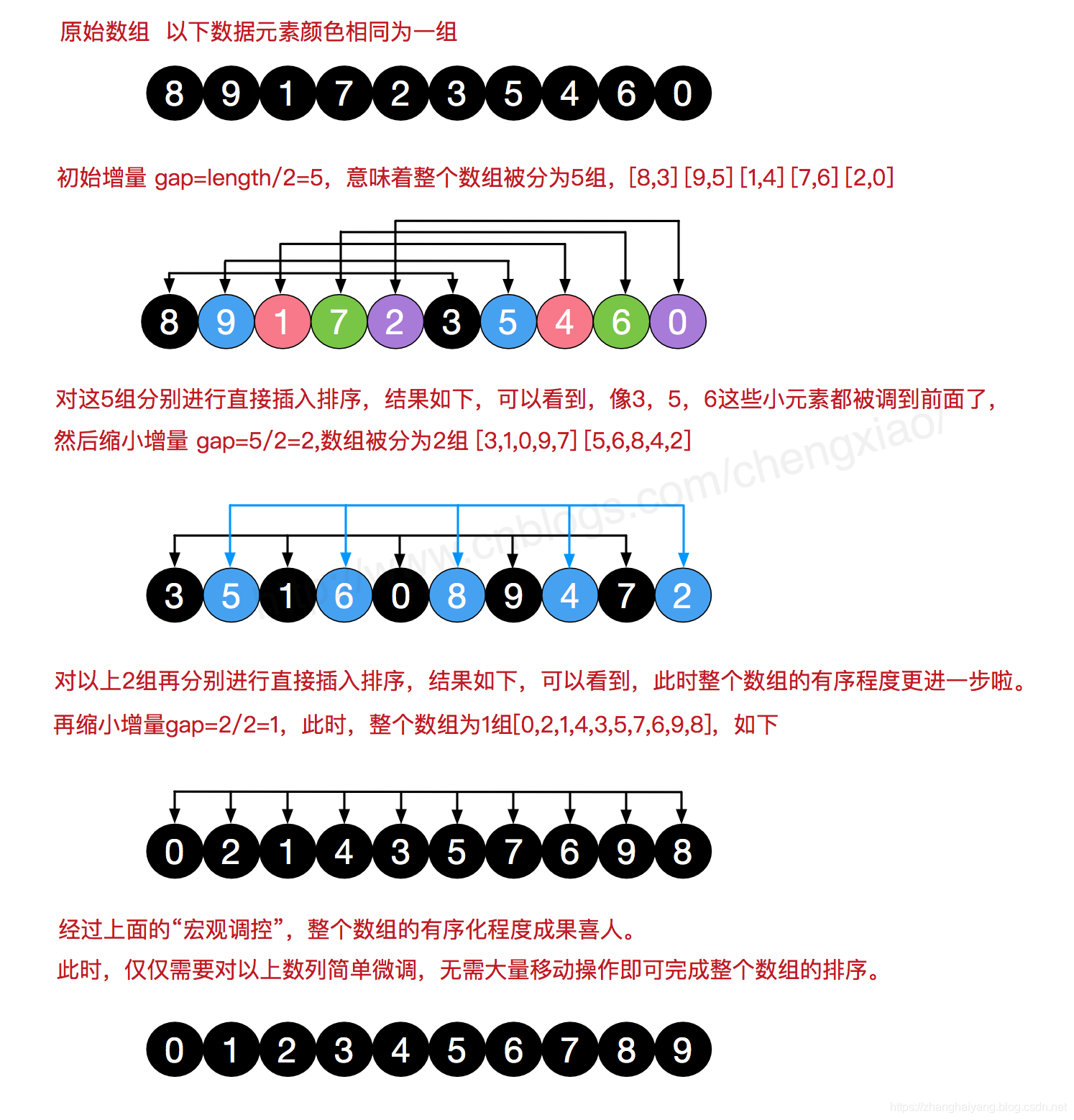
希尔排序.png

代码实现

  1. package sort;
  3. import java.util.Arrays;
  5. public class ShellSort {
  6.     public static void main(String[] args) {
  7.         int[] test = {3,5,657,23,4,7,1,435};
  8.         System.out.println(Arrays.toString(shellSort(test)));
  9.     }
  11.     public static int[] shellSort(int[] array){
  12.        int j;
  13.        //此循环为增量序列的变化
  14.        for(int gap = array.length/2; gap>0;gap/=2){
  15.            //此循环找到各个组的元素进行插入排序
  16.            for(int i =gap;i<array.length;i++){
  17.                int temp = array[i];
  18.                //组内插入排序
  19.                for(j=i;j>=gap &&temp<array[j-gap];j-=gap){
  20.                    array[j] = array[j-gap];
  21.                }
  22.                array[j] = temp;
  23.            }
  24.        }
  25.        return array;
  26.     }
  27. }

算法分析

不需要大量的辅助空间，和归并排序一样容易实现。希尔排序是基于插入排序的一种算法， 在此算法基础之上增加了一个新的特性，提高了效率。希尔排序时间复杂度的下界是n*log2n。希尔排序没有快速排序算法快 O(n(logn))，因此中等大小规模表现良好，对规模非常大的数据排序不是最优选择。但是比O(N)复杂度的算法快得多。并且希尔排序非常容易实现，算法代码短而简单。 此外，希尔算法在最坏的情况下和平均情况下执行效率相差不是很多，与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法. 本质上讲，希尔排序算法是直接插入排序算法的一种改进，减少了其复制的次数，速度要快很多。 原因是，当n值很大时数据项每一趟排序需要移动的个数很少，但数据项的距离很长。当n值减小时每一趟需要移动的数据增多，此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。Shell算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列，可以准确地估算关键词的比较次数和对象移动次数。想要弄清关键词比较次数和记录移动次数与增量选择之间的关系，并给出完整的数学分析，今仍然是数学难题。

希尔排序最坏情形分析

希尔排序的运行时间依赖于增量序列的选择
(1)使用希尔增量时,希尔排序的最坏情形运行时间为Θ(N)
希尔增量:ht = N / 2, h[k+1] = h[k] / 2，即{N/2, (N / 2)/2, …, 1}
希尔增量的问题在于,这些增量对未必是互素的,因此较小的增量可能影响很小
(2)使用Hibbard增量的希尔排序的最坏情形运行时间为Θ(N)
与希尔增量的关键区别在于 ,相邻的增量间没有公因子

稳定性

由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。