基本概念

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

核心要点

插入排序由N-1趟排序组成
对于p=1到N-1趟,插入排序保证从位置0到位置p上的元素为已排序状态
插入排序利用了这样的事实:已知位置0到位置p-1上的元素已经处于排过序的状态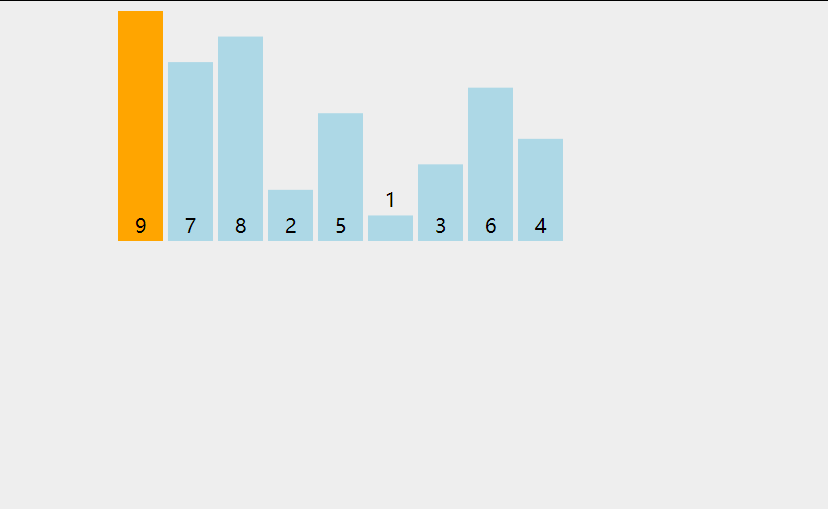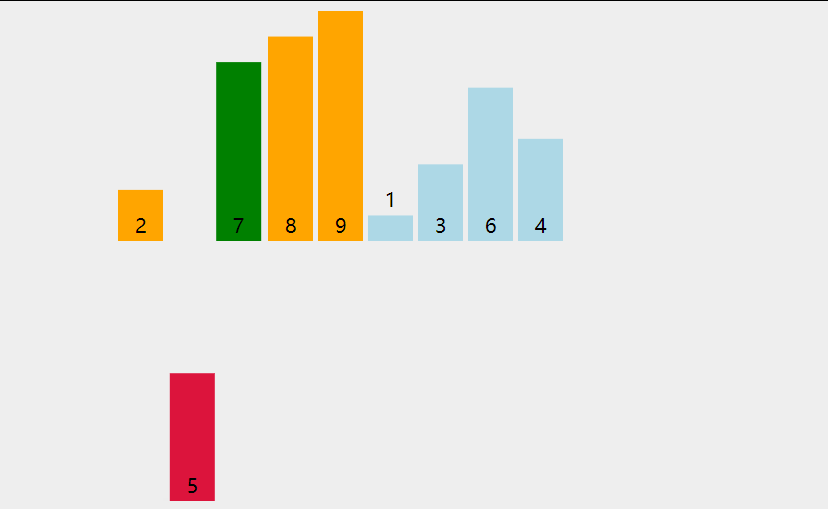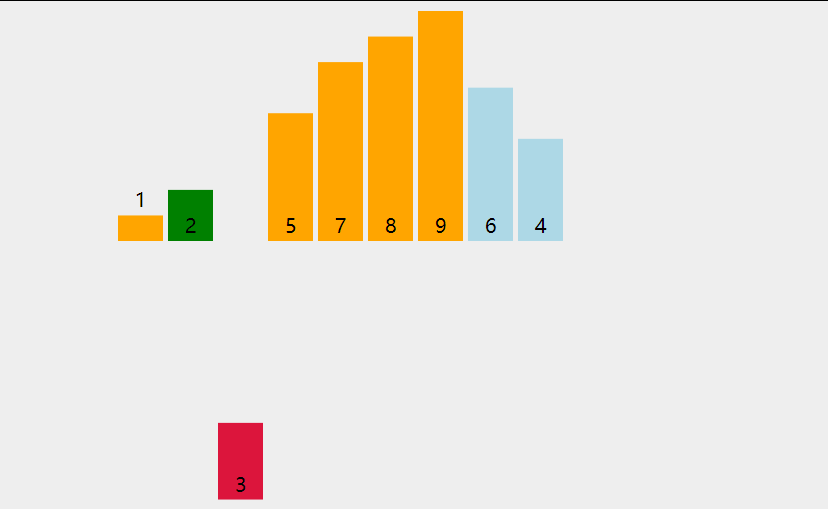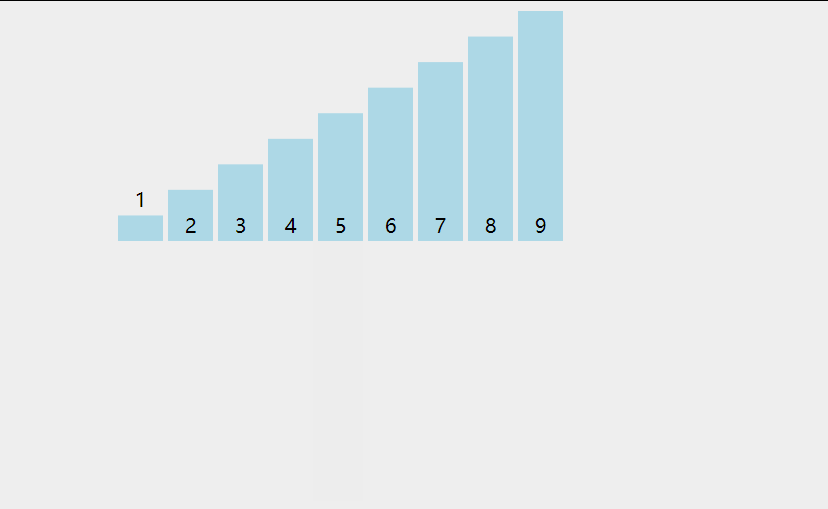
插入排序 - 图1

代码实现

  1. package sort;
  3. import java.lang.reflect.Array;
  4. import java.util.Arrays;
  6. public class insertionSort {
  7.     public static void main(String[] args) {
  8.         //构建测试用例
  9.         //功能测试：正常数组
  10.         //边界值测试：只有一个值的数组等
  11.         //性能测试：倒序数组
  12.         //异常测试：空数组等
  13.         int[] test = {7,34,546,7,12,3,65,23,6745};
  14.         System.out.println(Arrays.toString(test));
  15.         System.out.println(Arrays.toString(insertSort(test)));
  16.     }
  18.     public static int[] insertSort(int[] array){
  19.         if(array.length==0){
  20.             return array;
  21.         }
  22.         for (int i = 0; i < array.length -1; i++) {
  23.             int pre = i;
  24.             int current = array[i+1];
  25.             while(pre>=0&&current<array[pre]){
  26.                 array[pre+1] = array[pre];
  27.                 pre--;
  28.             }
  29.             array[pre+1] = current;
  30.         }
  31.         return array;
  32.     }
  33. }

算法分析

由于嵌套循环的每一个都花费N次迭代,因此插入排序为O(N),
(1)这个界是精确的,因为以反序的输入可以达到该界.
(2)如果输入数据已预先排序,那么运行时间为O(N),因为内层for循环的检测总是立即判定不成立而终止.
(3)插入排序的平均情形也是Θ(N)

复杂度分析

时间复杂度

在插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较N- 1次，时间复杂度为O(N)
最坏的情况是待排序数组是逆序的，此时需要比较次数最多，总次数记为：1+2+3+…+N-1，所以，插入排序最坏情况下的时间复杂度为O(N)
平均来说，A[1..j-1]中的一半元素小于A[j]，一半元素大于A[j]。插入排序在平均情况运行时间与最坏情况运行时间一样，是输入规模的二次函数 。

空间复杂度

插入排序的空间复杂度为常数阶O(1)

稳定性分析

如果待排序的序列中存在两个或两个以上具有相同关键词的数据，排序后这些数据的相对次序保持不变，即它们的位置保持不变，通俗地讲，就是两个相同的数的相对顺序不会发生改变，则该算法是稳定的；如果排序后，数据的相对次序发生了变化，则该算法是不稳定的。关键词相同的数据元素将保持原有位置不变，所以该算法是稳定的

应用分析

插入排序适用于已经有部分数据已经排好，并且排好的部分越大越好。一般在输入规模大于1000的场合下不建议使用插入排序