二分查找

704.二分查找

https://leetcode-cn.com/problems/binary-search/

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件

写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

二分法第一种写法
第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。
区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

  • while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=

  • if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1 ```java

    // 二分法第一种写法 public int search1(int[] nums, int target) {

    1.   // 左闭右开
    2.   int L = 0;
    3.   int R = nums.length;
    4.   int mid = 0;
    5.   while (L < R) {
    6.       mid = (L + R) >> 1;
    7.       if (nums[mid] > target) {
    8.           R = mid;
    9.       } else if (nums[mid] < target) {
    10.           L = mid + 1;
    11.       } else {
    12.           return mid;
    13.       }
    14.   }
    15.   return -1;

    }

  1. **二分法第二种写法**<br />如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。<br />有如下两点：
  3. - while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
  4. - if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
  5. ```java
  6. // 二分法第二种写法
  7. public int search2(int[] nums, int target) {
  8.     // 左闭右闭
  9.     int L = 0;
  10.     int R = nums.length - 1;
  11.     int mid = 0;
  12.     while (L <= R) {
  13.         mid = (L + R) >> 1;
  14.         if (nums[mid] > target) {
  15.             R = mid - 1;
  16.         } else if (nums[mid] < target) {
  17.             L = mid + 1;
  18.         } else {
  19.             return mid;
  20.         }
  21.     }
  22.     return -1;
  23. }

35.搜索插入位置

https://leetcode-cn.com/problems/search-insert-position/

  1.  public int searchInsert(int[] nums, int target) {
  2.      //左闭右开
  3.      int L = 0;
  4.      int R = nums.length;
  5.      int mid = 0;
  6.      while (L < R) {
  7.          mid = (L + R) >> 1;
  8.          if (nums[mid] > target) {
  9.              R = mid;
  10.          } else if (nums[mid] < target) {
  11.              L = mid + 1;
  12.          } else {
  13.              return mid;
  14.          } 
  15.      }
  16.      return L;
  17.  }

34.在排序数组中查找元素的第一个和最后一个位置

https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/

把所有情况都讨论一下。
寻找target在数组里的左右边界，有如下三种情况：

  • 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
  • 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
  • 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

这三种情况都考虑到，说明就想的很清楚了。
接下来，在去寻找左边界，和右边界了。
采用二分法来去寻找左右边界，为了让代码清晰，分别写两个二分来寻找左边界和右边界。

  1.  public int[] searchRange(int[] nums, int target) {
  2.         int[] res = new int[]{-1, -1};
  3.         res[0] = findLeftBoard(nums, target);
  4.         res[1] = findRightBoard(nums, target);
  5.         return res;
  6.     }
  8.     // 找左边界
  9.     private int findLeftBoard(int[] nums, int target) {
  10.         //左闭右开
  11.         int L = 0;
  12.         int R = nums.length;
  13.         int mid = 0;
  14.         int location = -1;
  15.         while (L < R) {
  16.             mid = (L + R) >> 1;
  17.             if (nums[mid] > target) {
  18.                 R = mid;
  19.             } else if (nums[mid] < target) {
  20.                 L = mid + 1;
  21.             } else { // ==
  22.                 R = mid;
  23.                 location = mid;
  24.             }
  25.         }
  26.         return location;
  27.     }
  29.     // 找右边界
  30.     private int findRightBoard(int[] nums, int target) {
  31.         //左闭右开
  32.         int L = 0;
  33.         int R = nums.length;
  34.         int mid = 0;
  35.         int location = -1;
  36.         while (L < R) {
  37.             mid = (L + R) >> 1;
  38.             if (nums[mid] > target) {
  39.                 R = mid;
  40.             } else if (nums[mid] < target) {
  41.                 L = mid + 1;
  42.             } else { // ==
  43.                 L = mid + 1;
  44.                 location = mid;
  45.             }
  46.         }
  47.         return location;
  48.     }

69.Sqrt(x)

https://leetcode-cn.com/problems/sqrtx/
比如Sqrt(104),
104的开方肯定比104小，
所以就从1 ~ 104这个范围二分，
每次找到mid， 然后让mid的平方与104比较，

  • 若mid的平方 > 104, 说明找大了， 再去左边二分
  • 若mid的平方 < 104, 说明找小了，再去右边二分
  • 若mid的平方 = 104，说明找到了一个暂定的结果，记录，但是我们还要看能不能再找一个离104更近的，所以再去右边二分

所以第二和第三种情况是可以合并的 

  1. public int mySqrt(int x) {
  2.     if (x == 0) return 0;
  3.     long L = 1;
  4.     long R = x;
  5.     long ans = 1;
  6.     while (L < R) {
  7.         long mid = (L + R) >> 1;
  8.         if (mid * mid > x) {
  9.             R = mid;
  10.         } else if (mid * mid <= x) {
  11.             L = mid + 1;
  12.             ans = mid;
  13.         }
  14.     }
  15.     return (int)ans;
  16. }

367. 有效的完全平方数

https://leetcode-cn.com/problems/valid-perfect-square/

  1. public boolean isPerfectSquare(int num) {
  2.     if (num == 1) {
  3.         return true;
  4.     }
  5.     long L = 1;
  6.     long R = num;
  7.     while (L < R) {
  8.         long mid = (L + R) >> 1;
  9.         if (mid * mid < num) {
  10.             L = mid + 1;
  11.         } else if (mid * mid > num) {
  12.             R = mid;
  13.         } else {
  14.             return true;
  15.         }
  16.     }
  17.     return false;
  18. }

移除元素

数组移除元素用的比较多的就是双指针 | 快慢指针

27. 移除元素

https://leetcode-cn.com/problems/remove-element/

  1.  public int removeElement(int[] nums, int val) {
  2.      int last = nums.length - 1;
  3.      int i = 0;
  4.      while (i < last) {
  5.        if (nums[i] == val) {
  6.          swap(nums, i, last--);
  7.        }else {
  8.          i++;
  9.        }
  10.      }
  11.      return last;
  12. }
  14. private void swap(int[] nums, int i, int j) {
  15.     int tmp = nums[i];
  16.     nums[i] = nums[j];
  17.     nums[j] = tmp;
  18. }

26. 删除有序数组中的重复项

https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/
快慢指针

  1.  public int removeDuplicates(int[] nums) {
  2.      int slow = 0;
  3.      int fast;
  4.      for (fast = 1;  fast < nums.length; fast++) {
  5.          if (nums[fast] != nums[slow]) {
  6.              slow++;
  7.              swap(nums, slow, fast);
  8.          }
  9.      }
  10.      return slow + 1;
  11.  }
  13. private void swap(int[] nums, int i, int j) {
  14.     int tmp = nums[i];
  15.     nums[i] = nums[j];
  16.     nums[j] = tmp;
  17. }

283. 移动零

**_https://leetcode-cn.com/problems/move-zeroes/

  1.  //双指针
  2. // 两个原则
  3. //  1) fast位置是0， fast++
  4. //  2) fast位置不是0. fast位置跟slow的下一个数交换， fast++， slow++
  5. public void moveZeroes(int[] nums) {
  6.     int slow = -1;
  7.     int fast;
  8.     for (fast = 0; fast < nums.length; fast++) {
  9.         if (nums[fast] != 0) {
  10.             swap(nums, ++slow, fast);
  11.         }
  12.     }
  13. }
  15. private void swap(int[] nums, int i, int j) {
  16.     int tmp = nums[i];
  17.     nums[i] = nums[j];
  18.     nums[j] = tmp;
  19. }

844. 比较含退格的字符串

https://leetcode-cn.com/problems/backspace-string-compare/

  • 双指针解法

    1. public boolean backspaceCompare(String s, String t) {
    2.       char[] S = s.toCharArray();
    3.       char[] T = t.toCharArray();
    4.       int i = s.length() - 1;
    5.       int j = t.length() - 1;
    6.       int Iskip = 0;
    7.       int Jskip = 0;
    9.       while (i >= 0 || j >= 0) {
    10.           while (i >= 0) {
    11.               if (S[i] == '#') {
    12.                   Iskip++;
    13.                   i--;
    14.               } else if (Iskip > 0) {
    15.                   Iskip--;
    16.                   i--;
    17.               } else {
    18.                   break;
    19.               }
    20.           }
    22.           while (j >= 0) {
    23.               if (T[j] == '#') {
    24.                   Jskip++;
    25.                   j--;
    26.               } else if (Jskip > 0) {
    27.                   Jskip--;
    28.                   j--;
    29.               } else {
    30.                   break;
    31.               }
    32.           }
    34.           if (i >= 0 && j >= 0) {
    35.               if (S[i] != T[j]) {
    36.                   return false;
    37.               }
    38.           } else {
    39.               if (i >= 0 || j >= 0) {
    40.                   return false;
    41.               }
    42.           }
    43.           i--;
    44.           j--;
    45.       }
    46.       return true;
    47.   }

  • 栈解法

    1. // 栈解法
    2.   public boolean backspaceCompare(String s, String t) {
    3.       char[] S = s.toCharArray();
    4.       char[] T = t.toCharArray();
    5.       return process(S).equals(process(T));
    6.   }
    8.   public String process(char[] str) {
    9.       Stack<Character> stack = new Stack<>();
    10.       for (char c : str) {
    11.           if (c == '#') {
    12.               if (!stack.isEmpty()) {
    13.                   stack.pop();
    14.               }
    15.           } else {
    16.               stack.push(c);
    17.           }
    18.       }
    19.       return stack.toString();
    20.   }

    有序数组的平方

    https://leetcode-cn.com/problems/squares-of-a-sorted-array/
    注意利用题目中是有序数组这一特点

  • 若原数组全为非负数， 那么平方后，数组仍是升序的

  • 若原数组全为负数， 那么平方后，数组是降序的
  • 若原数组既有负数又有正数，那么平方后，数组是先降序后升序的

双指针解法

  1. public int[] sortedSquares(int[] nums) {
  2.         int N = nums.length;
  3.         int[] ans = new int[N];
  4.         int pos = N - 1;
  5.         for (int i = 0, j = N - 1; i <= j; ) {
  6.             if (nums[i] * nums[i] < nums[j] * nums[j]) {
  7.                 ans[pos] = nums[j] * nums[j];
  8.                 j--;
  9.             } else {
  10.                 ans[pos] = nums[i] * nums[i];
  11.                 i++;
  12.             }
  13.             pos--;
  14.         }
  15.         return ans;
  16. }

长度最小/大的子数组

209. 长度最小的子数组

  • 滑动窗口解法

    1. public int minSubArrayLen(int target, int[] nums) {
    2.       int L = 0;
    3.       int sum = 0;
    4.       int len = Integer.MAX_VALUE;
    5.       for (int R = 0; R < nums.length; R++) {
    6.           sum += nums[R];
    7.           while (sum >= target) {
    8.               len = Math.min(len, R - L + 1);
    9.               sum -= nums[L++];
    10.           }
    11.       }
    12.       return len == Integer.MAX_VALUE ? 0 : len;
    13.   }

    904. 水果成篮

    https://leetcode-cn.com/problems/fruit-into-baskets/

  • 滑动窗口解法

    1. public int totalFruit(int[] fruits) {
    2.       int L = 0;
    3.       HashMap<Integer, Integer> map = new HashMap<>();
    4.       int ans = 0;
    5.       for (int R = 0; R < fruits.length; R++) {
    6.           map.put(fruits[R], map.containsKey(fruits[R]) ? map.get(fruits[R]) + 1 : 1);
    7.           while (map.size() >= 3) {
    8.               map.put(fruits[L], map.get(fruits[L]) - 1);
    9.               if (map.get(fruits[L]) == 0) {
    10.                   map.remove(fruits[L]);
    11.               }
    12.               L++;
    13.           }
    14.           ans = Math.max(ans, R - L + 1);
    15.       }
    16.       return ans;
    17.   }

    76. 最小覆盖子串

    https://leetcode-cn.com/problems/minimum-window-substring/
    滑动窗口 + 欠债表

  • 欠债表

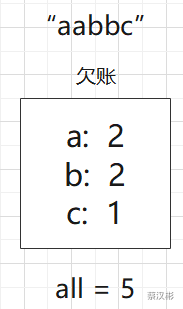
image.png
all是欠款总数量
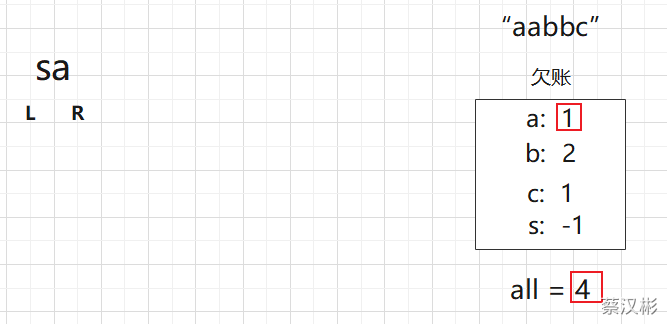
image.png
image.png
image.png
只要减减后，不小于0，就是有效还款，all也要减减，
若小于0则是无效还款，all不变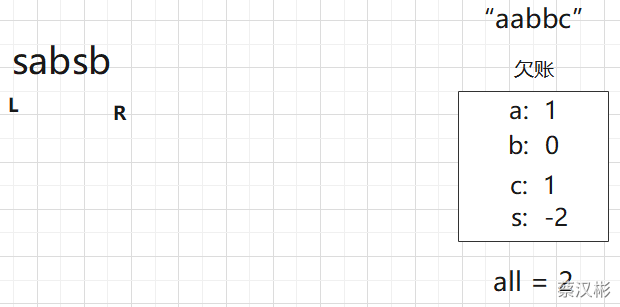
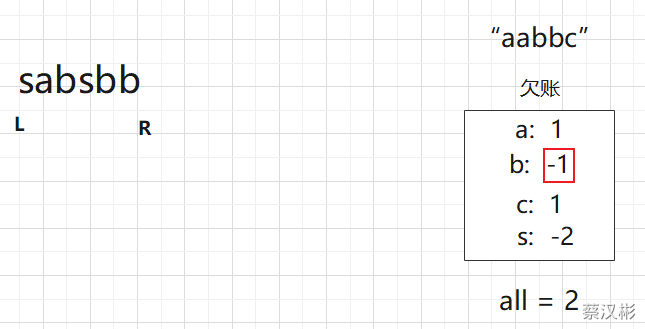
image.png
image.png
image.png
image.png
image.png

第一次all变成0的时刻，记录窗口长度，此时窗口的含义是如果子串必须以0开头，至少多长才能包含所有的字符，
后面的先别管，L开始缩
image.png
以1开头，记录窗口长度，然后L继续缩
image.png
欠款了, 让R往右继续
。。。
。。
。。

补充：coding细节， 窗口设置成左闭右开的，初始值就很容易设置， [0, 0) 就表示这个窗口一开始没数

  1. public static String minWindow(String s, String t) {
  2.         if (s.length() < t.length()) {
  3.             return "";
  4.         }
  5.         char[] str = s.toCharArray();
  6.         char[] target = t.toCharArray();
  7.         int[] map = new int[256];
  8.         int all = target.length;
  9.         int L = 0;
  10.         int R = 0;
  11.         int minLen = -1;
  12.         int ansL = -1;
  13.         int ansR = -1;
  14.         for (char c : target) {
  15.             map[c]++;
  16.         }
  17.         while (R != str.length) {
  18.             map[str[R]]--;
  19.             if (map[str[R]] >= 0) { // 有效还款
  20.                 all--;
  21.             }
  22.             if (all == 0) {
  23.                 while (map[str[L]] < 0) {
  24.                     map[str[L++]]++;
  25.                 }
  26.                 if (minLen == -1 || minLen > R - L + 1) {
  27.                     minLen = R - L + 1;
  28.                     ansL = L;
  29.                     ansR = R;
  30.                 }
  31.                 all++;
  32.                 map[str[L++]]++;
  33.             }
  34.             R++;
  35.         }
  36.         return minLen == -1 ? "" : s.substring(ansL, ansR + 1);
  37.     }

螺旋矩阵

59. 螺旋矩阵Ⅱ

https://leetcode-cn.com/problems/spiral-matrix-ii/

  • 这是正方形的矩阵

    1. public int[][] generateMatrix(int n) {
    2.       int[][] res = new int[n][n];
    3.       int leftRow = 0;
    4.       int leftCol = 0;
    5.       int rightRow = n - 1;
    6.       int rightCol = n - 1;
    7.       int count = 1;
    8.       while (leftRow <= rightRow && leftCol <= rightCol) {
    9.           if (leftRow == rightRow) { // 正方形矩阵只用额外判断这里即可
    10.               for (int i = leftCol; i <= rightCol; i++) {
    11.                   res[leftRow][i] = count++;
    12.               }
    13.           }else {
    14.               for (int i = leftCol; i < rightCol; i++) {
    15.                   res[leftRow][i] = count++;
    16.               }
    17.               for (int i = leftRow; i < rightRow; i++) {
    18.                   res[i][rightCol] = count++;
    19.               }
    20.               for (int i = rightCol; i > leftCol ; i--) {
    21.                   res[rightRow][i] = count++;
    22.               }
    23.               for (int i = rightRow;i > leftRow ; i--) {
    24.                   res[i][leftCol] = count++;
    25.               }
    26.           }
    28.           leftRow++;
    29.           leftCol++;
    30.           rightRow--;
    31.           rightCol--;
    32.       }
    33.       return res;
    34.   }

    54. 螺旋矩阵

    https://leetcode-cn.com/problems/spiral-matrix/

    1.  public List<Integer> spiralOrder(int[][] matrix) {
    2.       int leftRow = 0;
    3.       int leftCol = 0;
    4.       int rightRow = matrix.length - 1;
    5.       int rightCol = matrix[0].length - 1;
    6.       List<Integer> list = new ArrayList<>();
    7.       while (leftRow <= rightRow && leftCol <= rightCol) {
    8.           if (leftRow == rightRow ) { // 正方形矩阵额外判断的地方
    9.               for (int i = leftCol; i <= rightCol; i++) {
    10.                   list.add(matrix[leftRow][i]);
    11.               }
    12.           } else if (leftCol == rightCol) { // 还有可能是长方形矩阵
    13.               for (int i = leftRow; i <= rightRow; i++) {
    14.                   list.add(matrix[i][leftCol]);
    15.               }
    16.           } else {
    17.               for (int i = leftCol; i < rightCol; i++) {
    18.                   list.add(matrix[leftRow][i]);
    19.               }
    20.               for (int i = leftRow; i < rightRow; i++) {
    21.                   list.add(matrix[i][rightCol]);
    22.               }
    23.               for (int i = rightCol; i > leftCol; i--) {
    24.                   list.add(matrix[rightRow][i]);
    25.               }
    26.               for (int i = rightRow; i > leftRow; i--) {
    27.                   list.add(matrix[i][leftCol]);
    28.               }
    29.           }
    30.           leftRow++;
    31.           leftCol++;
    32.           rightRow--;
    33.           rightCol--;
    34.       }
    35.       return list;
    36.   }

    剑指Offer29. 顺时针打印矩阵

    https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/

    1. public int[] spiralOrder(int[][] matrix) {
    2.       if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
    3.           return new int[0];
    4.       }
    5.       int leftRow = 0;
    6.       int leftCol = 0;
    7.       int rightRow = matrix.length - 1;
    8.       int rightCol = matrix[0].length - 1;
    9.       int[] ans = new int[matrix.length * matrix[0].length];
    10.       int index = 0;
    11.       while (leftRow <= rightRow && leftCol <= rightCol) {
    12.           if (leftRow == rightRow) {
    13.               for (int i = leftCol; i <= rightCol; i++) {
    14.                   ans[index++] = matrix[leftRow][i];
    15.               }
    16.           } else if (leftCol == rightCol) {
    17.               for (int i = leftRow; i <= rightRow; i++) {
    18.                   ans[index++] = matrix[i][leftCol];
    19.               }
    20.           } else {
    21.               for (int i = leftCol; i < rightCol; i++) {
    22.                   ans[index++] = matrix[leftRow][i];
    23.               }
    24.               for (int i = leftRow; i < rightRow; i++) {
    25.                   ans[index++] = matrix[i][rightCol];
    26.               }
    27.               for (int i = rightCol; i > leftCol; i--) {
    28.                   ans[index++] = matrix[rightRow][i];
    29.               }
    30.               for (int i = rightRow; i > leftRow; i--) {
    31.                   ans[index++] = matrix[i][leftCol];
    32.               }
    33.           }
    34.           leftRow++;
    35.           leftCol++;
    36.           rightRow--;
    37.           rightCol--;
    38.       }
    39.       return ans;
    40.   }

    总结

    在面试中，数组是必考的基础数据结构。
    其实数据的题目在思想上一般比较简单的，但是如果想高效，并不容易。
    我们之前一共讲解了四道经典数组题目，每一道题目都代表一个类型，一种思想。

    二分法

    循环不变量原则，只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。

    双指针法

    双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

  • 暴力解法时间复杂度：$O(n^2)$

  • 双指针时间复杂度：$O(n)$

    滑动窗口

主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。
滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将$O(n^2)$的暴力解法降为$O(n)$。
如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

模拟行为

模拟类的题目在数组中很常见，不涉及到什么算法，就是单纯的模拟，十分考察大家对代码的掌控能力。
在这道题目中，我们再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。
相信大家又遇到过这种情况： 感觉题目的边界调节超多，一波接着一波的判断，找边界，踩了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的，大家可以在这道题目中体会到这一点。