【以下均来源代码随想录】

理论基础

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的，

解题步骤

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

1.斐波那契数

  • 递归

    1. public int fib(int n) {
    2.       if (n <= 1) {
    3.           return n;
    4.       }
    6.       return fib(n - 1) + fib(n - 2);
    7. }

  • 动态规划

    1. public int fib(int n) {
    2.       if (n <= 1) {
    3.           return n;
    4.       }
    5.       int[] dp = new int[n + 1];
    6.       dp[0] = 0;
    7.       dp[1] = 1;
    8.       for (int i = 2; i <= n; i++) {
    9.           dp[i] = dp[i - 1] + dp[i - 2];
    10.       }
    11.       return dp[n];
    12. }

2.爬楼梯

  1. public int climbStairs(int n) {
  2.         if (n <= 2) {
  3.             return n;
  4.         }
  5.         int[] dp = new int[n + 1];
  6.         dp[1] = 1;
  7.         dp[2] = 2;
  8.         for (int i = 3; i <= n; i++) {
  9.             dp[i] = dp[i - 1] + dp[i - 2];
  10.         }
  11.         return dp[n];
  12. }

3.使用最小花费爬楼梯⭐

  1. 确定dp数组以及下标的含义
  • dp[i]的定义：到达第i个台阶所花费的最少体力为dp[i]。（注意这里认为是第一步一定是要花费）
  1. 确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。
那么究竟是选dp[i-1]还是dp[i-2]呢？
一定是选最小的，所以dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
注意这里为什么是加cost[i]，而不是cost[i-1],cost[i-2]之类的，因为题目中说了：每当你爬上一个阶梯你都要花费对应的体力值

  1. dp数组如何初始化

根据dp数组的定义，dp数组初始化其实是比较难的，因为不可能初始化为第i台阶所花费的最少体力。
那么看一下递归公式，dp[i]由dp[i-1]，dp[i-2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。

  1. public int minCostClimbingStairs(int[] cost) {
  2.         int[] dp = new int[cost.length];
  3.         dp[0] = cost[0];
  4.         dp[1] = cost[1];
  6.         for (int i = 2; i < cost.length; i++) {
  7.             dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
  8.         }
  9.         return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
  10. }

4.不同路径

动态规划

  1.  public int uniquePaths(int m, int n) {
  2.         int[][] dp = new int[m][n];
  3.         for (int j = 0; j < n ; j++) {
  4.             dp[m - 1][j] = 1;
  5.         }
  7.         for (int i = 0; i < m; i++) {
  8.             dp[i][n - 1] = 1;
  9.         }
  11.         for (int i = m - 2; i >= 0; i--) {
  12.             for (int j = n - 2; j >= 0 ; j--) {
  13.                 dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
  14.             }
  15.         }
  16.         return dp[0][0];
  17.  }

数论⭐

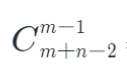
image.png
image.png

  • 组合公式:
    • image.png
  1.      /**
  2.      * 数论
  3.      */
  4.     public int uniquePaths(int m, int n) {
  5.         int all = m + n - 2;
  6.         int part = all - (m - 1);
  7.         long o1 = 1;
  8.         long o2 = 1;
  9.         for (int i = part + 1, j = 1; i <= all && j <= m - 1; i++, j++) {
  10.             o1 *= i;
  11.             o2 *= j;
  12.             long gcd = gcd(o1, o2);
  13.             o1 /= gcd;
  14.             o2 /= gcd;
  15.         }
  16.         return (int) (o1 / o2);
  18.     }
  20.     //辗转相除法
  21.     private long gcd(long o1, long o2) {
  22.         return o2 == 0 ? o1 : gcd(o2, o1 % o2);
  23.     }

5.不同路径Ⅱ

  1.  public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  2.         int M = obstacleGrid.length;
  3.         int N = obstacleGrid[0].length;
  4.         //dp[i][j]含义：从i，j出发到右下角有几条路径
  5.         int[][] dp = new int[M][N];
  6.         for (int i = M - 1; i >= 0; i--) {
  7.             if (obstacleGrid[i][N - 1] == 1) {
  8.                 break;
  9.             } else {
  10.                 dp[i][N - 1] = 1;
  11.             }
  12.         }
  14.         for (int i = N - 1; i >= 0 ; i--) {
  15.             if (obstacleGrid[M - 1][i] == 1) {
  16.                 break;
  17.             } else {
  18.                 dp[M - 1][i] = 1;
  19.             }
  20.         }
  22.         for (int i = M - 2; i >= 0; i--) {
  23.             for (int j = N - 2; j >= 0 ; j--) {
  24.                 if (obstacleGrid[i][j] == 0) {
  25.                     dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
  26.                 }
  27.             }
  28.         }
  29.         return dp[0][0];
  31.  }

6.整数拆分

  1. public int integerBreak(int n) {
  2.         //dp[i] 拆分数字i可以得到的最大乘积
  3.         int[] dp = new int[n + 1];
  4.         dp[2] = 1;
  5.         for (int i = 3; i <= n ; i++) {
  6.             //拆分出的第一个数是j，固定
  7.             for (int j = 1; j < i - 1; j++) {
  8.                 //可能性1：只拆分成两个数
  9.                 //可能性2：拆分成多个数
  10.                 dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
  11.             }
  12.         }
  13.         return dp[n];
  14.     }

7.不同的二叉搜索树⭐

  • 注意本题是二叉搜索树

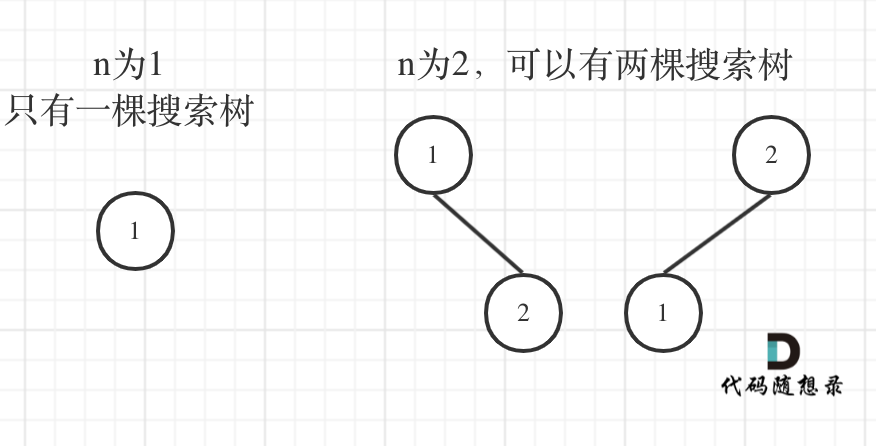
image.png
n为1的时候有一棵树，n为2有两棵树，这个是很直观的。
image.png
来看看n为3的时候，有哪几种情况。
当1为头结点的时候，其右子树有两个节点，看这两个节点的布局，是不是和 n 为2的时候两棵树的布局是一样的啊！
（可能有人问了，这布局不一样啊，节点数值都不一样。别忘了我们就是求不同树的数量，并不用把搜索树都列出来，所以不用关心其具体数值的差异）
当3为头结点的时候，其左子树有两个节点，看这两个节点的布局，是不是和n为2的时候两棵树的布局也是一样的啊！
当2为头结点的时候，其左右子树都只有一个节点，布局是不是和n为1的时候只有一棵树的布局也是一样的啊！
发现到这里，其实我们就找到了重叠子问题了，其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里，这道题目就有眉目了。
dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] dp[0] + dp[1] dp[1] + dp[0] dp[2]
如图所示：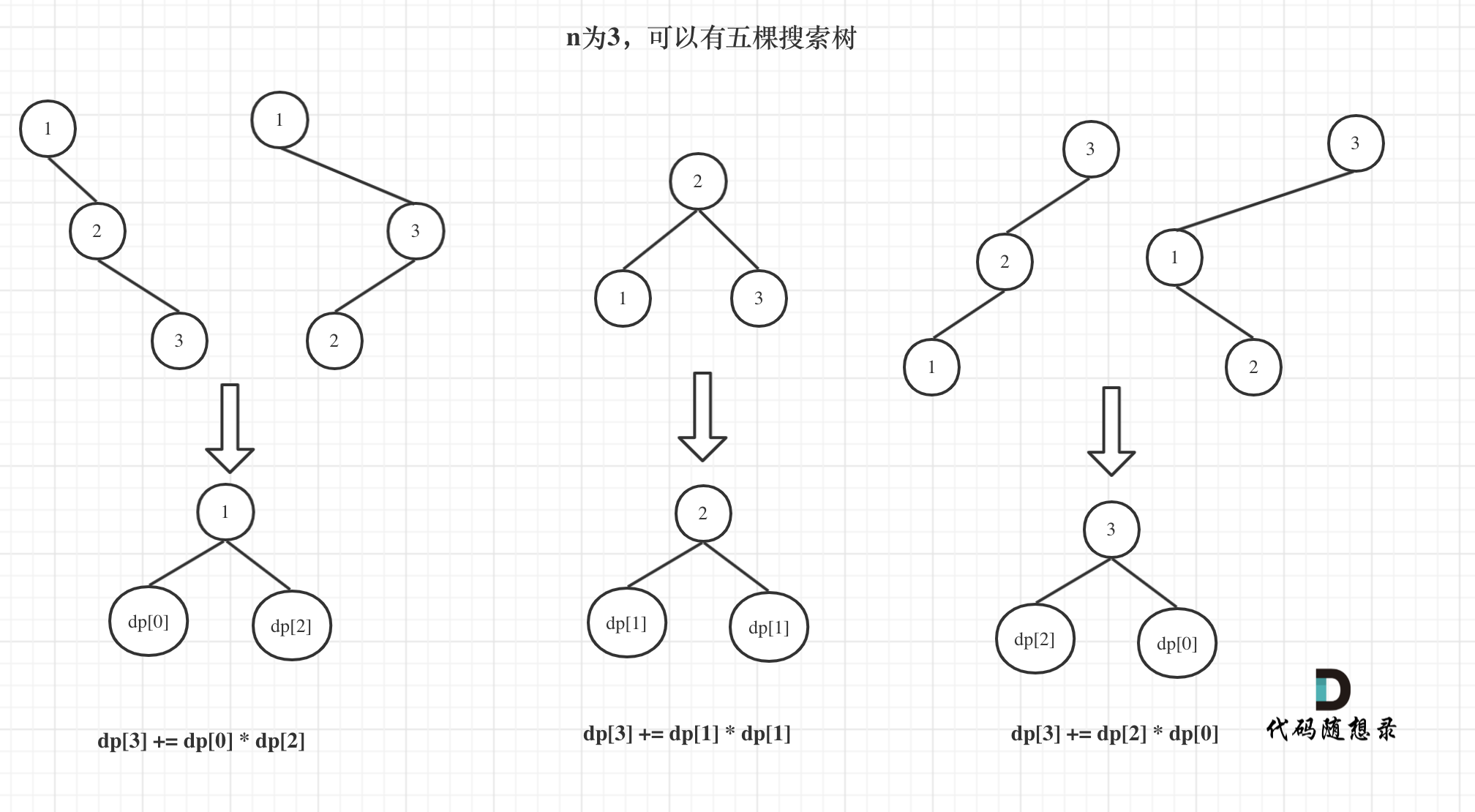
image.png

  1. public int numTrees(int n) {
  2.         //dp[i] 从1到i可以组成几种二叉搜索树
  3.         int[] dp = new int[n + 1];
  4.         dp[0] = 1;
  5.         for (int i = 1; i <= n; i++) {
  6.             //以j为头
  7.             for (int j = 1; j <=i ; j++) {
  8.                 dp[i] += dp[j - 1] * dp[i - j];
  9.             }
  10.         }
  11.         return dp[n];
  12. }